
이번엔 본격적으로
여러가지 사건들과 이를 확률로 표현하는 방법
그리고 확률의 기본 연산원리를 공부할것이다.
- 여러가지 사건 -
표본공간 S의 부분집합인 두 사건 A, B가 있다고 해보자.
여기서 사건 A 또는 사건 B가 일어나는 사건
즉 A가 일어나거나 B가 일어나는 사건
이것을 A와 B의 '합사건'이라 하고
A∪B 라고 표현한다.
여기서 사건 A와 사건 B가 동시에 일어나는 사건
즉 A도 일어나고 B도 일어나는 사건
이것을 A와 B의 '곱사건'이라 하고
A∩B 라고 표현한다.
두 사건 A와 B가 절대로 동시에 일어날수 없을때
A와 B는 서로 '배반사건'이라고 한다.
즉 A∩B = Ø 이다.
예를 들어, 한개의 주사위에서 1의 눈이 나오면서
동시에 2의 눈이 나올수 없다.
따라서 1이 나오는 사건과
2가 나오는 사건은 배반사건이다.
사건 A에 대하여
A가 일어나지 않는 사건을 A의 '여사건'이라 하고

위와 같이 표현한다.
여기서 여사건의 '여'는 남을 여(餘) 이다.
즉 사건 A를 빼고 남는 사건, 나머지 사건
정도로 이해하면 쉽다.
왜 표현법이 영어 C냐면
여사건이 영어로 complementary event이다.
예를 들어, 한개의 주사위를 던졌을때
2 이하의 눈이 나오는 사건을 A라 하면
A = {1, 2} 이다.
그리고 A의 여사건은
2 이하의 눈이 나오지 않는 사건이고
따라서 아래와 같다.

추가로,
사건 A와 사건 A의 여사건은 동시에 일어날 수 없다.
여사건의 정의가 A가 일어나지 않는 사건 이기 때문이다.
따라서 아래 식이 성립한다.

한줄요약하면 다음과 같다.
'어떤 사건과 그것의 여사건의 곱사건은 공사건이다.'
예제로 정리하고 넘어간다.
주사위 한개를 던질 때,
나오는 눈이 3 이하인 사건을 A
나오는 눈이 2 이상인 사건을 B
라고 하겠다.
1. 사건 A 또는 사건 B가 일어날 사건, 즉 A와 B의 합사건은?
2. 사건 A와 B가 동시에 일어날 사건, 즉 A와 B의 곱사건은?
3. 사건 A의 여사건은?
4. 사건 A의 여사건과 사건 B의 곱사건은?
사건 A = {1, 2, 3}
사건 B = {2, 3, 4, 5, 6}
1. 따라서 A와 B의 합사건은
{1, 2, 3, 4, 5, 6}
2. 따라서 A와 B의 곱사건은
{2, 3}
3. 따라서 사건 A의 여사건은
{4, 5, 6}
4. 사건 A의 여사건이 A = {4, 5, 6} 이므로
사건 A의 여사건과 사건 B의 곱사건은
{4, 5, 6}
- 확률의 덧셈정리 -
표본공간 S의 부분집합인 두 사건 A, B에 대하여
이 두 사건과 확률의 덧셈연산의 관계를 다룬다.
그리고 이 내용은 벤다이어그램을 이용하는게
이해가 쉽다.
난 실제로 수능문제에 확률의 덧셈정리 문제가 나오면
덧셈정리 공식이 아니라 벤다이어그램으로 푼다.
여기서 A 또는 B 가 일어날 확률을 구해보자.
즉 A와 B의 합사건의 확률을 구해보자는것
우선 표본공간 S, 두 사건 A, B를 벤다이어그램으로 표현하면
아래와 같이 된다.

A와 B의 합사건이라는건

A 또는 B 니까 회색으로 칠한부분이다.
이 부분을 구하는 방법은

A사건을 더한 뒤

B사건도 더해준다.
그런데 여기서

녹색 부분은 두번 더해졌다.
원래는 한번만 더해져야 회색부분의 넓이가 나오는거기 때문에
저 녹색부분을 한번 빼줘야한다.
그리고 저 녹색부분은
A와 B가 같이 일어나는 사건
즉 A와 B의 곱사건 이다.
따라서 A와 B의 합사건은 다음과 같다.

여기서 확률의 수학적 정의를 가져오면
확률의 덧셈정리가 유도된다.

여기서 질문이 있을수 있다.
A와 B가 배반사건이면?

A와 B가 겹치는 부분
즉 A와 B가 동시에 일어나는
A와 B의 곱사건 이 공사건이기 때문에
여기서 A와 B의 합사건은
그냥 A와 B를 더하면 된다.

여기서 공식들을 외우지 말자.
내가 벤다이어그램을 괜히 그려준게 아니다.
왜 이런 식이 나오는지를 알려준거고
난 형식적으로 일단 공식이 있긴하니까 적어준것 뿐이다.
- 예제 -
1 )
두 사건 A, B에 대하여
P(A) = 1/8 이고 P(B) = 1/2 이다.
A와 B가 배반사건일 경우, P(A∪B)는?
1. 벤다이어그램 풀이

2. 공식 풀이

따라서 답은 5/8
보면 알겠지만
벤다이어그램으로 푸는게
더 직관적이라 실수할일이 거의 없다.
2 )

1. 벤다이어그램 풀이
우선 A와 B의 곱사건의 확률이 0이 아니기때문에
A와 B는 배반사건이 아니다.

따라서 다음과 같이 되고

따라서 답은 5번
2. 공식풀이

따라서 답은 5번
- 여사건의 확률 -
말 그대로 여사건이 일어날 확률을 구하는거다.
이런게 왜 필요하냐면
이런 문제가 나왔다고 해보자.
동전 A, B를 동시에 던진다.
던져진 동전은 앞면 또는 뒷면이 나온다.
둘중 적어도 하나는 앞면이 나올 확률은?
그럼 여기서 확률을 구하려면
둘중 적어도 하나는 앞면이 나오는 경우의 수를 구해야 할것이다.
그럼 A가 앞면이 나오는 경우, B가 앞면이 나오는 경우 를 각각 구해야하고
이 두 경우를 그냥 더하면
A와 B가 둘다 앞면이 나오는 경우를 두번 더한게 되기때문에
이것까지 구해서 한번 빼줘야한다.
참 번거롭다.
이정도는 할수있다고 치자
근데 동전 10개를 던져도 이렇게 할건가?
동전 A가 앞면이 나오는경우 B가 앞면 C가 앞면 D가 앞면
A랑B가 앞면 B랑C가 앞면 이런식으로?
이건 너무 많고 복잡하다. 너무 비효율적이다.
왜 비효율적이냐면
'적어도' 하나는 앞면이 나오는 경우를 구하는거라서
하나가 앞면이 나올수도 있고
두개가 앞면이 나올수도 있고
세개가 앞면이 나올수도 있고
경우의 수를 나눠서 생각해야하는데 너무 많아지기 때문이다.
근데 이를 한줄로 줄이는 방법이 있다.
'적어도' 하나는 앞면이 나오는 경우를 구하고싶으면
하나도 앞면이 나오지 않는경우
즉 전체 경우에서 모두 뒷면이 나오는 경우를 제외하면
'적어도' 하나는 앞면이 나오는 경우가 나올거 아닌가?
즉 전체 경우에서 모두 뒷면이 나오는 경우를 빼주면 된다는거다.
앞면이 '적어도 1개' 라는건
앞면이 0개인거 빼고 전부 라는 말이기 때문이다.
이는 다시말해서 전체 경우의 수에서 '여사건'의 경우의 수를 빼준다는 말이다.
동전 두개를 던졌으니
전체 경우의 수는 {앞앞, 앞뒤, 뒤앞, 뒤뒤} 로 4이고
모두 뒷면이 나오는 경우의 수는 1 이므로
모두 뒷면이 나올 확률은 1/4 이다.
따라서 적어도 하나는 앞면이 나올 확률은
1 - 1/4 = 3/4 이다.
이런식으로 구하는거다.
일반화 하자면,
사건 A에 대해
사건 A가 일어날 확률 P(A)를 구하라는데
사건 A가 일어나는 경우의 수를 구하려니 너무 많고 복잡해서
사건 A가 일어나지 않는 경우의 수를 구하는게 더 쉬운경우
A의 여사건이 일어나는 경우의 수를 구한다음 전체 경우의 수에서 빼주는게
효율적인 방법이 될수 있다.
그리고 여기서 사용되는 기본 논리는

사건 A가 일어날 확률과
사건 A가 일어나지 않을 확률을 더하면 1이 된다는것이다.
너무 당연한게
A가 일어나거나 일어나지 않을 확률은
당연히 1이다.
여사건의 확률을 이항하면 공식 완성

요약하자면,
어떤 사건의 경우의 수를 구하려는데
그것보다 여사건의 경우의 수를 구하는게 더 쉬운경우
여사건의 경우의 수를 구한뒤

이 논리를 이용하여 구하면 된다.
- 예제 -

1. 여사건의 확률로 풀이
임의로 2개의 공을 꺼낼때
흰공이 적어도 1개 이상일 확률이니까
전체 경우의 수에서 흰공을 0개 꺼내는 경우의 수를 빼면 된다.
즉 전체에서 여사건을 뺀다.

여기서 전체 경우의수, 즉 표본공간 S는
공 7개중 임의로 2개를 꺼내는것
즉 7개중 2개를 선택하는것
따라서 n(S)는
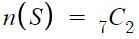
그리고 흰공을 0개 꺼내는 경우의 수는
공을 2개 꺼낼건데 검은공만 2개 꺼내는 경우의 수이고
검은공이 4개니까
A의 여사건의 경우의 수는

따라서 각각 대입하면

따라서

따라서 답은 5번
2. 여사건 없이 풀이
공을 2개 꺼내는데
적어도 흰공이 1개이상일 확률이니까
흰공이 1개인 경우
흰공이 2개인 경우
이 두개로 나눠야한다.
흰공이 1개인 경우는
흰공 1개 검은공 1개 꺼낸거다.
흰공 1개 검은공 1개 꺼내는 경우의 수는
흰공 3개중 하나니까 3
검은공 4개중 하나니까 4
따라서 3×4 = 12
다음으로 흰공이 2개인 경우는
흰공 3개중 2개 뽑는거니까
₃C₂ = 3
따라서 적어도 흰공이 1개이상일 경우의 수는
12+3 = 15
그리고 전체 경우의 수는
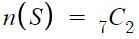
이거니까 21
따라서 답은

따라서 답은 5번
여기서는 공을 2개 뽑는거라
여사건을 이용해 풀지 않아도 그리 복잡하지 않았지만
여사건을 이용해 푸는게 훨씬 효율적인건 부정할수 없다.
어떤 상황에서 여사건을 이용해 푸는게 효율적인지
딱 잘라서 말할수는 없고 문제를 풀어보면서 감을 익혀야한다.
'확률과 통계 > II. 확률' 카테고리의 다른 글
| 독립시행 #2 - 독립시행의 확률 (0) | 2021.12.08 |
|---|---|
| 독립시행 #1 - 독립사건과 종속사건 (0) | 2021.12.07 |
| 조건부확률 (0) | 2021.12.07 |
| 확률의 수학적 정의와 기본 성질 (0) | 2021.12.03 |



