
- 최댓값과 최솟값 -
최댓값 : 어떤 함수의 함숫값 중에서 가장 큰 값
말그대로 가장 큰값
최솟값 : 어떤 함수의 함숫값 중에서 가장 작은 값
말그대로 가장 작은값
- 이차함수의 최댓값, 최솟값 구하는법 -
처음엔 그래프를 그려서 해결할것이다.
그리고 이 글을 다 읽을때 쯤엔 그래프 안그리고도 해결할수 있게된다.
무조건 해야하는 핵심적인 풀이법은
'꼭짓점을 찾는것' 이다.
그래프를 그리는 방법이 처음 배우는 사람에게 더 쉽기도 하고,
안그리는 풀이법도 매끄럽게 이해가 가능하기때문에
그래프를 그리는 방법부터 보여줄것이다.
- 그래프 그려서 해결하기 -

저 이차함수의 그래프부터 그려보겠다.
그래프를 그리려면 '꼭짓점'을 찾아야한다.
따라서 저 식을 '표준형'으로 바꿔서 다시써야한다.

바꿔서 다시 썼다.
이제 꼭짓점이 어딘지 보인다.
(-1, 2) 이다.
그리고 이차항의 계수가 양수이므로
꼭짓점을 기준으로 위로 올라가는 모양의
그래프가 그려질것이다.

따라서 여기서 최솟값은 바로 보인다.
꼭짓점을 기준으로 계속 올라가므로,
꼭짓점이 최솟값을 갖는곳이다.
따라서 최솟값은 2이다.
그런데 최댓값은?
함숫값이 끝없이 올라가는데 그럼 무한인가?
무한이 최댓값은 아니다.
무한은 값이 얼마라고 정할수 없다.
무한 = 끝이 없다
즉 끝없이 큰숫자라는것
어떤 숫자를 말하든 거기서 1만 더하면
그것보다 큰 숫자가 되어버리기 때문에
여기서 최댓값은 무한히 큰 수라는 표현만 있을 뿐
값을 특정지어 말할수 없다.
따라서 이럴때는
'최댓값은 정의되지 않는다.'
또는
'최댓값은 존재하지 않는다'
라고 해야한다.
따라서 이 문제의 답은
최댓값 : 없음, 최솟값 : 2
- 연습 -

꼭짓점은 (-6, -7) 이며
이차항의 계수가 음수이므로
꼭짓점을 기준으로 내려가는 모양의
그래프가 그려질것이다.

꼭짓점을 기준으로 계속 내려가므로,
꼭짓점이 최댓값을 갖는곳이다.
따라서 최댓값은 -7이다.
그리고 계속 내려가므로,
최솟값은 정의할수 없다.
따라서 답은
최솟값 : 없음, 최댓값 : -7
- 그래프 안그리고 해보자 -

꼭짓점은 (-6, -7)
그리고 최고차항은 음수
따라서 꼭짓점에서 최댓값을 갖고
최댓값은 -7이다.
그리고 최솟값은 존재하지 않는다.
내가 처음에 '핵심은 꼭짓점을 찾는것이다'
라고 했던 이유가 여기서 밝혀졌다.
꼭짓점의 위치만 알면
그곳을 기준으로 올라가거나 내려가기 때문에
거기가 최댓값이 되거나, 최솟값이 된다.
- 제한된 범위에서의 최대, 최소 -
말 그대로,
x값의 범위가 제한된 상태에서 최대, 최소를 구하는거다.
예를 들어, 0≤x≤4 에서 이차함수 y=x² 의 최댓값을 구하시오. 하면
원랜 끝없이 올라가기때문에 최댓값이 없지만
이번엔 끝없이 올라가지 못하도록 범위를 잘라놨기 때문에
x=4 까지밖에 못올라가고
따라서 x=4에서 최댓값을 갖게 되는거다.
여기서는 두가지 케이스가 있다.
1. 꼭짓점이 범위 안에 있는경우
2. 꼭짓점이 범위 밖에 있는경우
하지만 여기서도 푸는 핵심 논리는
이차함수의 그래프는 꼭짓점을 기준으로 좌우대칭이며,
이차항의 계수에 따라서
꼭짓점을 기준으로 올라가는지 내려가는지 정해진다.
그냥 이것만 알면 어떤 문제가 나와도 다 풀린다.
한문제만 푸는걸 보여주겠다.

우선 꼭짓점을 찾기 위해 표준형으로 바꾸면
x²+4x+2 = (x+2)²-2
따라서 꼭짓점은 (-2, -2) 이며
이차항의 계수가 양수이므로 꼭짓점이 최저점이다.
근데 x값의 범위가 제한되어있으므로 이것까지 생각해야한다.
x값의 범위가 -3≤x≤0 인데
꼭짓점인 (-2, -2)는 여기에 포함된다.
따라서 최솟값은 꼭짓점부분이고, -2이다.
최댓값은, 범위가 제한되어있지 않았다면 존재하지 않았을텐데
범위가 있으므로 끝없이 올라가지 않고 중간에 멈출것이다.
여기서 핵심은, 꼭짓점에서 멀어질수록 큰 값이 될것이다.
주어진 범위 -3≤x≤0 에서
꼭짓점에서 가장 먼곳은 x=0 이다.
따라서 x=0에서 최댓값을 가지며,
그 값은 2이다.
따라서 답은
최댓값 : 2 , 최솟값 : -2
아직 익숙치 않아서 헷갈린다면
그래프를 그려서 풀면 된다.

- 예제 -
1 )

꼭짓점을 찾기 위해, 식을 표준형으로 바꾸면
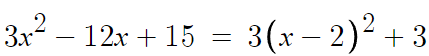
따라서 꼭짓점은 (2, 3) 이고
이차항이 양수이므로
꼭짓점이 최저점이다.
따라서 답은
최댓값 : 없음, 최솟값 : 3
헷갈리면 그래프 그려서 풀어도 된다.
2 )

우선 꼭짓점을 찾기 위해, 식을 표준형으로 만든다.
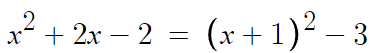
따라서 꼭짓점은 (-1, -3) 이다.
그리고 이차항의 계수가 양수이다.
따라서 꼭짓점인 (-1, -3)이 f(x)의 최저점이다.
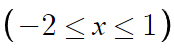
그리고 문제에서 준 범위 내에 꼭짓점이 존재한다.
따라서 최솟값은 꼭짓점인 -3이다.
그리고 최댓값은
꼭짓점에서 가장 먼 곳
따라서 x=1 에서 최댓값을 갖고
x=1을 대입하면 최댓값은 1이다.
따라서 답은
최댓값 : 1, 최솟값 : -3
헷갈리면 그래프 그려봐도 된다.
3 )

우선 꼭짓점을 찾기 위해, 식을 표준형으로 만든다.
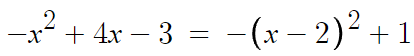
따라서 꼭짓점은 (2, 1) 이다.
그리고 이차항의 계수가 음수이다.
따라서 꼭짓점인 (2, 1)이 f(x)의 최고점이다.
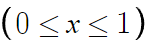
그런데 문제에서 준 범위 내에 꼭짓점이 존재하지 않는다.
그래도 상관없다.
꼭짓점에서 멀어질수록 함숫값이 작아진다.
라는것만 이해하고 있다면 풀수있다.
따라서 저 범위 내에서
꼭짓점에서 가장 가까운곳이 최대이고
가장 먼곳이 최소이다.
가장 가까운곳은 x=1 이고
따라서 최댓값은 x=1 대입하면 0
가장 먼곳은 x=0 이고
따라서 최솟값은 x=0 대입하면 -3
따라서 답은
최댓값 : 0, 최솟값 : -3
물론 헷갈리면 그래프 그려봐도 된다.
그래프를 그려보면 더 직관적인 이해가 가능하다.
'수학(상) > II. 방정식' 카테고리의 다른 글
| 연립이차방정식 (0) | 2022.02.05 |
|---|---|
| 고차방정식의 풀이 (0) | 2022.02.03 |
| 이차함수 #3 - 이차함수의 그래프 그리기와 평행이동 (0) | 2022.01.28 |
| 이차함수 #2 - 이차함수의 그래프와 직선의 위치 관계 (0) | 2022.01.26 |
| 이차함수 #1 - 이차방정식과 이차함수의 관계 (0) | 2022.01.25 |



