
- 개요 -
별거 없는곳이다.
중학교때도 연립방정식 풀어봤었을텐데
그냥 하던대로 하면된다.
중학교수학에서 하는건 일차방정식을 연립하는거고
여기서는 이차방정식을 연립할거다.
- 연립이차방정식의 기본 풀이법 -

이런 문제를 풀건데
연립방정식을 푸는 방법은 두가지 정도가 있다.
1. 가감법 : 두 방정식을 서로 더하거나 빼서 두 문자중 하나를 소거시킨다.
2. 대입법 : 두 문자 사이의 관계식을 세운 다음 방정식에다가 대입해서 푼다.
근데 이런 문제에서는 가감법을 사용할수가 없는게
어떻게 더하고 빼도 x나 y를 소거시킬수가 없다.
즉 여기선 가감법 풀이가 안된다.
따라서 여기서 사용할 방법은 대입법 이다.
한번 풀어줄테니 따라오기만 하면 된다.
어려운게 없다.

요약하자면,
더하거나 빼서 풀수 없으니
그냥 두 문자의 관계식을 세운다음 대입해버린다.
그러면 한 문자에 대한 이차방정식이 되고
그러면 풀수 있다.
- 연습 -

- 심화 : 이차방정식과 이차방정식의 연립 -
우리가 지금까지 한건
일차방정식과 이차방정식의 연립이다.
그리고 고등학교수학에서는 여기까지만 다룬다.
그럼 이차방정식과 이차방정식은 어떻게 연립하냐?
일단 문제를 보자.

우리는 이차방정식과 이차방정식을 연립하는 방법을 모른다.
하지만 일차방정식과 이차방정식을 연립하는 방법은 안다.
따라서 여기서 사용되는 아이디어가 뭐냐면
이차식은 두 일차식의 곱 아닌가?
그니까 (이차식) = (일차식)×(일차식) 아닌가?
그리고 이차방정식에서 우변을 0으로 만들어버리면
(일차식)×(일차식) = 0
결국 이런식으로 나올것이다.
두 일차식중 하나는 무조건 0이다.
이게 핵심이다.
일단 보여주겠다.

따라서 아래와 같이 바뀐다.

위의 방정식 (x-2y)(x+y) = 0 을 만족하려면
x-2y=0 이거나 x+y=0 이어야한다.
따라서 아래와 같이 쓸수 있다.

따라서 아까 하던
일차방정식과 이차방정식의 연립
이 과정을 두번 해야된다.
Q. 그러면 x, y 근이 네 쌍이나 나오지 않나요?
그렇다. 네 쌍이나 나온다. 좀 귀찮지만 어쩔수 없다.
웬만하면 한번 풀어주고싶지만
어차피 하던거 두번하면 되는 문제기도 하고
솔직히 나도 귀찮아서 못적어주겠다.
알아야 할것은
'이차식을 인수분해 한다는것'이다.
왜 인수분해하는지는 아까도 설명했지만
일차방정식과 이차방정식의 연립은 할줄 알기때문에
일차방정식과 이차방정식의 연립 식이 되도록 유도하는것이다.
요약하자면,
이차방정식과 이차방정식을 연립하는건 못하지만
일차방정식과 이차방정식을 연립하는건 할수있다.
따라서 이차방정식중에서
하나를 골라서 두 일차식의 곱 꼴로 인수분해 한다음
두 일차식중 하나는 무조건 0이어야함을 이용해서
일차방정식과 이차방정식의 연립 식을 두개 세운다음
둘다 푼다.
Q. 인수분해가 안되면 어떡하나요?
인수분해가 안되는 이차식을 문제로 제시하면
고등학교수학 수준으로 못풀기때문에
그런 문제는 나오지 않는다.
- 예제 -
1 )

일단 연립방정식을 푸는법은
가감법, 대입법 정도가 있는데
가감법으로는 풀이가 불가능해보이니
대입법으로 풀어봐야겠다 라고 추론할수 있다.

2 )

이차방정식과 이차방정식을 연립해야한다.
그런건 우리가 못한다.
따라서 일차방정식과 이차방정식을 연립하게 되도록
식을 변형할 필요가 있다.
정확히 어떻게 변형하냐면
위쪽 식과 아래쪽 식중 하나를 인수분해해서 일차식×일차식 = 0 꼴로 만들거다.
위쪽 식과 아래쪽 식중 하나를 골라서 인수분해하면 된다.
위쪽 식이 합차공식 인수분해가 바로 보이니까 위쪽 식으로 가겠다.

따라서 x+y=0 또는 x-y=0 이다.
따라서 아래와 같이
두 연립방정식으로 변형된다.

왼쪽 연립방정식부터 풀어보자.
-왼쪽 연립방정식 풀이-

대입법을 사용하기 위해 위쪽 식을 변형하면 x=-y 이고
이를 아래쪽 식에 대입하면
(-y)² + (-y)y + 3y² = 15
정리하면, y² = 5
따라서 왼쪽 연립방정식의 근은

-오른쪽 연립방정식 풀이-

대입법을 사용하기 위해 위쪽 식을 변형하면 x=y 이고
이를 아래쪽 식에 대입하면
(y)²+y²+3y² = 15
정리하면 y² = 3
따라서 오른쪽 연립방정식의 근은
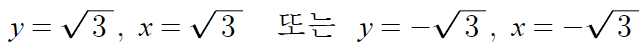
따라서 최종적인 답은

'수학(상) > II. 방정식' 카테고리의 다른 글
| 고차방정식의 풀이 (0) | 2022.02.03 |
|---|---|
| 이차함수 #4 - 이차함수의 최대, 최소 (0) | 2022.02.02 |
| 이차함수 #3 - 이차함수의 그래프 그리기와 평행이동 (0) | 2022.01.28 |
| 이차함수 #2 - 이차함수의 그래프와 직선의 위치 관계 (0) | 2022.01.26 |
| 이차함수 #1 - 이차방정식과 이차함수의 관계 (0) | 2022.01.25 |




