
- 개요 : 고차방정식이란? -
고차방정식이란, 최고차수가 삼차 이상인 다항방정식을 의미한다.
예를 들어, x³+x=1 이런게 고차방정식이다.
최고차수가 삼차이기 때문이다.
차수가 삼차(3차)인걸 삼차방정식,
사차(4차)인걸 사차방정식 이라 한다.
같은 논리로, 차수가 100차면 백차방정식이라 한다.
여기서 우리가 다룰건
삼차방정식과 사차방정식의 풀이이다.
- 삼차방정식, 사차방정식의 풀이 -
우리가 이차방정식을 어떻게 풀었는지를 복습해보자.
인수분해가 되면 인수분해해서 풀고,
잘 안되면 근의공식을 써서 풀었었다.
이것도 똑같다.
인수분해가 되면 인수분해해서 풀고,
잘 안되면 근의공식을 써서 풀면 된다.
근데 삼차, 사차방정식의 근의공식은
너무 복잡하기때문에 고등학교수학에선 다루지 않는다.
따라서 고등학교 수준에서 할수 있는건
'인수분해를 이용하는것' 뿐이고
따라서 다음과 같은 결론을 얻는다.
고차방정식은 인수분해를 이용해서 푼다.
근의공식은 너무 복잡해서 다루지 않는다.
이차방정식 풀때와 똑같은 논리를 그대로 적용하면 된다.

ABC=0 이라면
A와 B의 곱이 0이 되기 위해
A=0 이거나
B=0 이거나
C=0 이거나
A=B=0 이거나
B=C=0 이거나
A=C=0 이거나
A=B=C=0 이어야 한다.
아무튼 확실한건
'A, B, C중 하나는 무조건 0이다'
여기서 A, B, C 자리에
각각 일차식을 넣어볼까?
A = x-2 라 하고
B = x+3 이라 하고
C = x+5 라고 하면
A×B×C는 일차식×일차식×일차식 이니까 삼차식이 될것이다.

(x-2)(x+3)(x+5)=0 이라면
(x-2), (x+3), (x+5) 곱이 0이 되기 위해
(x-2)=0 이거나
(x+3)=0 이거나
(x+5)=0 이거나
(x-2)=(x+3)=0 이거나
(x+3)=(x+5)=0 이거나
(x-2)=(x+5)=0 이거나
(x-2)=(x+3)=(x+5)=0 이어야 한다.
아무튼 확실한건
'(x-2), (x+3), (x+5) 중 하나는 무조건 0이다'
x-2=0 을 만족시키는 x값은 2
x+3=0 을 만족시키는 x값은 -3
x+5=0 을 만족시키는 x값은 -5
따라서

이 식은 x=2 또는 x=-3 또는 x=-5
을 만족해야만 한다.
그래야 곱해서 0이 될수 있다.
따라서 이 방정식의 근은
x=2 , x=-3 , x=-5 이다.
- 연습 -

방정식이긴 한데 최고차수가 삼차이므로 고차방정식이다.
고차방정식은 어떻게 푼다?
인수분해해서 푼다.
근데 결과가 저렇게 나오는 인수분해공식이 떠오르지 않는다.
떠오르지 않으면 공통인수를 찾아보려 했는데
공통인수도 딱히 없다.
인수분해가 이도저도 안될때는 어떻게한다?
인수정리를 이용한다.
즉 하나씩 대입해본다.
x³-2x²+1
여기다 x=0 을 대입했더니 1이다. 따라서 0이 아니다.
여기다 x=1을 대입했더니 0이다.
따라서 인수정리에 의해
x³-2x²+1 은 (x-1) 을 인수로 갖는다.
x³-2x²+1를 (x-1)로 나누는건 조립제법을 이용하자.
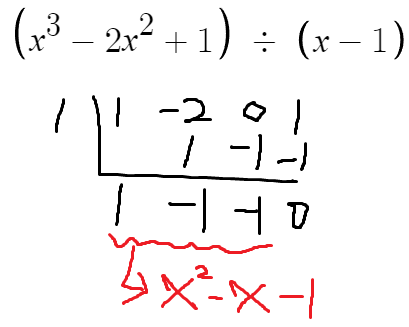
따라서 아래 식이 성립한다.
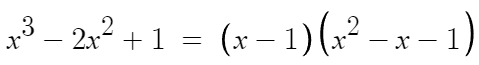
(x-1)=0 이거나 (x²-x-1)=0 이 되도록 하는 x값이 바로
이 방정식의 근이다.
이제 x²-x-1 의 근만 구하면 된다.
일단 인수분해공식 떠오르지않음
인수분해방법도 떠오르지않음
따라서 이걸 인수분해하려면
똑같이 하나하나 넣어봐야한다.
근데 이건 약간의 팁인데
이차식에서 인수분해방법이 안떠오를정도면
근이 분수나 루트로 돼있어서일 확률이 높다.
따라서 이런건 그냥 근의공식을 쓰는게 더 빠르다.
근의공식을 적용하면

역시나 루트가 들어가있다.
아까도 말했지만 이 방정식의 근은
(x-1)=0 이거나 (x²-x-1)=0 이 되도록 하는 x값
따라서 답은
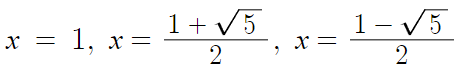
- 심화 : 특수한 형태인 사차방정식의 풀이 -
몰라도 큰 지장은 없지만
알면 더 빠르게 풀수 있다.
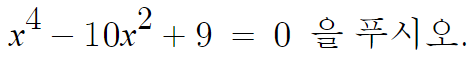
사실 이건 이미 알고있다.
인수분해만 할줄 알면 풀수있는데
저런 식을 인수분해하는법을 이미 배웠기 때문이다.
복습하자면, x²를 '치환'한다.
x²=A라고 치환하면
식이 아래와 같이 바뀐다.

이건 인수분해할수 있다. 인수분해하면 아래와 같이 된다.
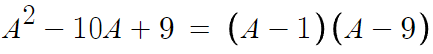
따라서 결론적으로
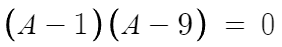
이걸 만족하는 A값을 찾은 뒤
A=x² 니까 그대로 x값으로 돌려주기만 하면 된다.
저걸 만족하는 A값은
A=1 또는 A=9
A=x² 이므로
x²=1 또는 x²=9
따라서 답은
x=1, x=-1, x=3, x=-3
- 예제 -
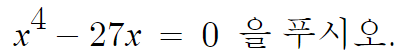
고차방정식은 인수분해해서 푼다.
공통인수 x가 보이니 묶어낸다.

x³-27 도 인수분해 해야하는데
x³-27도 고차방정식이기 때문에 얘도 인수분해해서 푼다.
인수분해공식 안보이고 공통인수 안보이니
인수정리를 이용한다. 즉 일일이 대입해본다.
그러면 x=3을 대입하면 x³-27=0 이 됨을 알수있다.
따라서 x³-27은 (x-3)을 인수로 갖는다.
x³-27을 x-3 으로 나누는건 조립제법을 이용하자.

따라서 여기까지 인수분해한걸 적으면
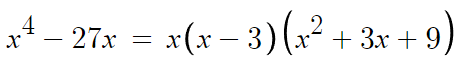
이제 x²+3x+9 의 근만 구하면 된다.
얘도 인수분해가 되면 좋겠지만
인수분해할 방법이 떠오르지 않는다.
따라서 근의공식을 쓴다.
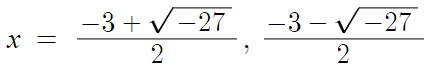
허수가 등장한다. 풀다보니 왜 인수분해가 안됐는지 알겠다.
아무튼 이제 정리하자면
x=0 또는 x-3=0 또는 x²+3x+9=0 이면 된다.
따라서 답은
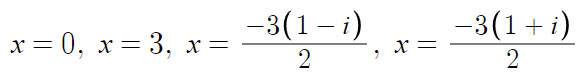
혹시 x=0, x=3 까지만 구했다면 틀린거다.
허근도 근이다. 실근만 구하라고 한적 없다.
'수학(상) > II. 방정식' 카테고리의 다른 글
| 연립이차방정식 (0) | 2022.02.05 |
|---|---|
| 이차함수 #4 - 이차함수의 최대, 최소 (0) | 2022.02.02 |
| 이차함수 #3 - 이차함수의 그래프 그리기와 평행이동 (0) | 2022.01.28 |
| 이차함수 #2 - 이차함수의 그래프와 직선의 위치 관계 (0) | 2022.01.26 |
| 이차함수 #1 - 이차방정식과 이차함수의 관계 (0) | 2022.01.25 |



