딱히 대단한 내용도 없고
특히 과탐 물리 선택자라면 날로 먹는 부분이다.
- 속도 -
영어로는 velocity이고 보통 v라고 쓴다.
수학적 정의는
'위치 변화를 시간 간격으로 나눈 값'이다.
수직선(x축) 위를 움직이는 점 P가 있다고 해보자.
그리고 이 점 P의 위치가 시간에 따라 달라질 때
즉 위치와 시간이 관련되어 있을 때
즉 위치를 시간에 대해 나타낼 수 있을 때
이 점 P의 위치를 x라 하면
x를 t에 대한 식으로 나타낼 수 있다.
x = f(t)
예를 들자면, 점 P가 원점에서 출발하여
x축 위에서 초속 2m/s 로 움직인다?
그러면 x = f(t) = 2t 인 것이다.
만약 점 P가
t=0초에서 t=5초까지
x=1에서 x=3 으로 움직였다 해보자.
움직인 경로는 상관없다.
f(0)=1 이고 f(5)=3 인 것이다.
따라서 이때의 평균속도를 구하자면
위치 변화량 = 나중위치 - 초기위치 = f(5)-f(0)
시간 간격 = 5-0
따라서 이것들을 이용하여 평균속도를 구한다는건
위치의 평균변화율을 이용한다는 것이다.
위치의 평균변화율을 구하면
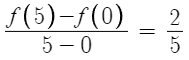
5초간 평균적인 위치 변화량이 2이다.
즉 평균속도가 2/5 이다.
근데 우리는 어떤 순간의 속도를 알고싶다.
t=3 이럴때의 속도를 알고싶은 것이다.
어떤 순간이라는건 매우 짧은 시간간격이니까
극한의 개념을 가져와야한다.
즉 순간속도를 정의할때는 미분계수가 이용된다.
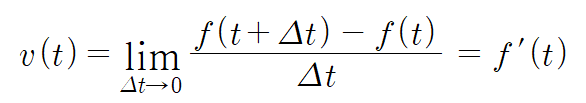
따라서 속도의 수학적 정의는 다음과 같다.
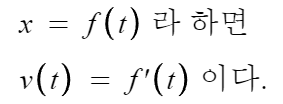
즉 위치를 미분한게 속도이다.
여기서 주의할건
보다시피 속도는 위치의 도함수이기 때문에
음수가 나올수도 있다.
속도가 음수가 나왔다는건
위치가 -x 방향으로 가고있다는것이다.
즉, 속도는 '방향'의 개념을 이미 내포하고 있다.
만약 +x방향을 양의 방향으로 잡았다면
물체가 +x방향으로 이동중일때는 속도가 양수가 나오고
-x방향으로 이동중일때는 속도가 음수로 나올것이다.
그리고 +x와 -x중 어디를 양의 방향으로 잡을지는 출제자 맘대로이니,
문제를 제대로 읽어야 실수 안한다.
따라서, 속도와 가속도 문제를 풀때,
물체의 운동 방향이 변한다거나 하는 표현이 나온다면
속도의 부호가 바뀌었구나. 라고 이해하면 되는거다.
- 가속도 -
영어로는 acceleration이고 보통 a라고 쓴다.
수학적 정의는
'속도 변화를 시간 간격으로 나눈 값'이다.
속도 = 위치 변화를 시간 간격으로 나눈 값
가속도 = 속도 변화를 시간 간격으로 나눈 값
따라서 위치 변화를 시간 간격으로 나눈 값의 변화를
시간 간격으로 나눈게 가속도이다.
조금 말이 어려운데 식으로 써보면 쉽다.
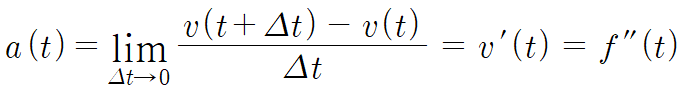
즉 속도를 미분한게 가속도다.
따라서 위치를 두번 미분하면 가속도가 된다.
여담으로
f''(t) 라는건
' ←이게 두개 붙어있는거다. 즉
f(t)를 t에 대해 두 번 미분했다는 뜻이다.
두번 미분한걸 이계도함수라고 하는데
이건 수학II가 아니라 미적분 과정이라서
몰라도 된다.
- 예제 -
1 )

x가 시각에 따른 식으로 나타내어 졌으므로
x = f(t)라 하면 시각에 따른 위치의 함수가 된다.
속도 = 위치를 미분한 것
따라서 v(t) = 2 일때의 f(t)값을 묻는 문제이다.
f(t) = -t^2 + 6t 이므로
v(t) = f'(t) = -2t + 6
따라서 v(t) = 2 가 되도록 하는 t = 2 이다.
따라서 이때 점 P의 위치는
f(2) = 8
따라서 답은 1번
2 )

가속도 = 속도를 미분한 것
속도 = 위치를 미분한 것
따라서 가속도 = 위치를 두 번 미분한 것
v(t) = f'(t) = 3t^2 - 12t
a(t) = 6t - 12
따라서 t=2 일때 가속도가 0이다.
따라서 이때의 속도는 v(2) = -12
따라서 답은 1번
'수학II > II. 미분' 카테고리의 다른 글
| 도함수의 활용 #2 - 함수의 증가와 감소, 함수의 극대와 극소 (0) | 2021.09.30 |
|---|---|
| 도함수의 활용 #1 - 접선의 방정식, 평균값 정리 (0) | 2021.09.28 |
| 미분가능성 (1) | 2021.09.28 |
| 미분계수와 도함수, 미분법 공식 (0) | 2021.09.27 |



