
저번엔 중복조합이 무엇인지,
계산은 어떻게 하는지 간단하게 알아봤다면
본격적인 문제풀이를 하는법을 알려주는 글이다.
- 1 : 전개식에서의 항의 개수 -
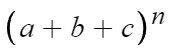
이걸 전개했을때
전개식에서의 서로다른 항의 개수는?
이게 왜 중복조합이냐면
위 식을 전개하는 과정에서
(a+b+c)(a+b+c)... 이런식으로 갈거 아닌가?
여기서 (a+b+c)(a+b+c)부터 전개해보자.
왼쪽부분의 a부터 곱셈의 분배법칙으로 전개해보면
a² + ab + ac 가 될 것이다.
여기서 각 항들은
a 입장에서 보면
자신과 곱해질 것을 a, b, c 중 하나를 선택한 결과물이다.
b랑 곱해지고 싶었으니까 ab 라는 결과가 나온것이다.
즉 여기서 a만 전개했을때 나오는 항의 개수는
'3개중 하나를 뽑는 행위'를 '1번' 진행한거기때문에 3개이다.
그럼 (a+b+c)(a+b+c)(a+b+c) 를 a만 전개해보자.
a는 a, b, c 중 무엇이랑 곱해질지 '선택' 하는 행위를
'두번' 할것이다.
그리고 여기서 선택되는 순서는 상관이 없다.
예를 들어,
a가 b랑 곱해진 뒤 a와 곱해진 경우인 ab × a 와
a가 a랑 곱해진 뒤 b와 곱해진 경우인 a² × b 는
결국 둘다 a²b로 같기 때문에
같은 경우로 취급해야한다.
즉 두번째에 곱해지는 b나 세번째에 곱해지는 b나
어차피 결과값은 똑같기때문에 안궁금하다는거다.
a가 몇개 곱해졌느냐? b가 몇개 곱해졌느냐? c가 몇개 곱해졌느냐?
이것이 항을 결정하는거다.
즉 최종 전개식에 있어서
곱해지는 순서는 관심이 없고 몇개 곱해졌는지만 궁금하다는거다.
즉 '몇개 곱해질지' 만 정해주면 되고
'곱해지는 순서'는 정하지 않아도 된다.
이는 배열하지 않아도 된다는말이고
따라서 이건 선택하기만 하면 되는 조합 임을 알수 있다.
그리고 a가 b랑 한번 곱해졌다고 또 b랑 곱해지지 말라는 법이 있는가?
없다. 중복을 허락한다는뜻이다.
따라서 조합이면서 중복을 허락하는거니까
결국 이건 중복조합이 되는것이다.
그래서 답이 뭐냐면
우선 곱해질것을 a, b, c 중 하나를 '선택' 한다.
즉 3개중 하나를 '선택'하는 행위를 하며
n 거듭제곱이므로
이 행위를 'n번' 한다.
따라서 중복을 허용하여 3개중 하나를 선택하는 행위를 n번 하는것이므로
저 문제의 답은

- 2 : 함수의 개수 -
집합 X = {1, 2, 3, 4} 에서 집합 Y = {2, 3, 4, 5} 로의 함수 f 중
집합 X의 임의의 두 원소 i, j 에 대하여 i < j 이면 f(i) ≤ f(j)
를 만족시키는 함수 f의 개수는?
뭔가 문제 생김새는 어마무시한데 사실 별거 아니다.

대충 이런 상황인데
우선 X에서 Y로의 함수 f이기 때문에
집합 X입장에서
각각의 원소가 선택할수있는 집합Y의 원소는 하나 뿐이다.
f(1)=2면서 f(1)=3 일수는 없지않은가?
즉 어떠한 X에 대응되는 Y가 하나뿐이라는거다.
따라서 X의 원소에게
Y의 원소중 어떤걸 택할거냐고 물어보는게 효율적이다.
먼저 X의 원소 1에게 물어보기를
Y 어떤 원소 원하냐 하면
2, 3, 4, 5 중에 고를텐데
만약 X의 원소 1이 Y원소 5를 택했다면
나머지 X의 원소 2, 3, 4는 조건을 만족하기 위해
선택의 여지 없이 무조건 5를 택해야한다.
즉 f(1)=5 라면
문제 조건을 만족시키기 위해 f(2)=f(3)=f(4)=5 여야한다.
만약 X의 원소 1이 Y원소 4를 택했다면
나머지 X의 원소 2, 3, 4는 조건을 만족하기 위해
Y원소중 4보다 크거나같은걸 적당히 택해야하는데
여기서 문제가 생긴다.
왜냐면 X의 원소 2가 4를 택한다면
X의 원소 3이 택할수 있는 Y의 원소는 4, 5 이고
X의 원소 3이 또 4를 골랐는지 5를 골랐는지에 따라서
X의 원소 4가 Y원소중 어떤걸 택할수있는지가 또 달라지고
참 복잡해진다.
X원소 1이 Y원소 4만 선택해도 이정도인데
X 원소 1이 Y 원소 2를 선택해버리면
정말 골치아파질것이다.
따라서 이 방법은 너무 복잡하고 비효율적이다.
그래서 여기서 이용할 아이디어가 뭐냐면
함수 Y의 원소중 어떤게 X에게 선택되는지
그리고 그것들이 몇개씩 선택되는지
이걸 구하면
어차피 문제 조건을 만족하기 위해
알아서 X의 원소들이 거기에 맞게 자리로 들어간다.
가령 뽑힌 Y의 원소가 2, 3, 5 이고
2는 2번 뽑혔고 3은 1번 뽑혔고 5는 1번 뽑혔다고 해보자.
그럼 꼼짝없이 f(1)=f(2)=2, f(3)=3, f(4)=5 이다.
i < j 이면 f(i) ≤ f(j) 여야하기 때문이다.
즉 Y의 원소중 어떤게 뽑히는지
그리고 각각 몇번 뽑히는지
그것만 정해주면 X의 원소들이 알아서 그것에 맞게 자리에 들어갈거라는거다.
따라서
X가 뽑을건 Y의 원소인데 Y의 원소가 4개니까
4개중에서 하나를 뽑을거고
X의 원소가 4개니까 이 행위를 4번 한다.
그리고 X 값이 달라도 Y 값이 같을수 있기때문에
Y의 원소를 뽑을때는 중복이 가능하다. 즉 중복이 허용된다.
따라서 Y의 원소 '4개'중 하나를 뽑는 행위를
'중복 허용'하여 '4번' 하는것이다.
따라서 이건 중복조합 문제이고, 답은
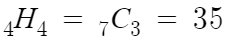
따라서 답은 35이다.
이제 일반화해보자.
집합 X의 원소의 개수는 m이고,
집합 Y의 원소의 개수는 n이다.
이때 X에서 Y로의 함수 f 에서
임의의 i, j에 대하여
i < j 이면 f(i) ≤ f(j) 를 만족시키는
함수 f의 개수는?
집합 Y의 원소 'n개'중 하나를 뽑는 행위를
집합 X의 원소의 개수인 'm번' 하고
중복을 허용하는거니까
답은 아래와 같다.

공식이라고 외우라는게 아니다.
단지 이런 문제를 풀때 쓰는 아이디어가
결론적으로 중복조합 문제였음을 알려주는 의미
그 이상도 이하도 아니다.
공식을 외우지 마라. 조금만 꼬아서내면 공식 적용못해서 못풀게 되니까
- 3 : 방정식을 만족시키는 정수 해 -
방정식 x+y+z+w=6 을 만족시키는
음이 아닌 정수해의 순서쌍 (x, y, z, w)의 개수는?
우선 음이 아닌 정수해이므로
0, 1, 2, ... 이런식으로 될것이다.
그리고 x+y+z+w=6 이거를
x+y+z+w = 1+1+1+1+1+1 이렇게 바꿔보자.
그러면 이 x y z w 의 값은
+1이 6개 있는데 이 +1 을 얘네한테 어떻게 나눠주냐에 따라 정해지는 값이다.
예를들어 x에 +1을 3개 나눠주면 x는 3이 되는것이다.
따라서 +1 6개를 x,y,z,w에 나눠주는 방법의 수를 구하면 된다.
즉 +1 입장에서는
x, y, z, w 중 하나로 가야하니까 4개중 하나 선택하는거다.
단 주의할게 +1 끼리는 구별이 안된다.
즉 x에 +1을 첫번째로 나눠주든
+1을 두번째로 나눠주든
결과는 어차피 x=1 이기 때문에
이를 같은 경우로 취급해야한다.
즉 +1을 배열하는건 의미가 없다. 어차피 구별이 안되기때문에
따라서 이는 +1이 어디로 갈지 '선택'만 하면 되는 문제임을 알 수 있고
+1이 x에 2번갈수도 있고 3번갈수도 있다는건
x를 여러번 뽑는걸 허용한다는거니까
이는 중복을 허용한다는걸 뜻한다.
따라서 이건 중복을 허용해서 선택하는 문제니까
중복조합 문제가 되는것이다.
풀이법은 간단하다.
+1 입장에서
x, y, z, w 중 하나 즉 '4개중 하나를 선택'한다.
그리고 그 행위를
+1이 6개 있으니까 '6회' 반복한다.
그리고 중복이 허용된다.
따라서 구하고자 하는 경우의 수는

따라서 답은 84
아래에 제시할 문제는 숫자 바꾸고 약간 심화한 예제이다.
x+y+z = 7 을 만족시키는 자연수해의 순서쌍 (x, y, z) 의 개수는?
아까랑 똑같이 하자.
x+y+z = 1+1+1+1+1+1+1 이다.
즉 +1 7개를 x, y, z에게 나눠주는거다.
근데 여기서 문제는
x, y, z가 0은 될수 없다. 문제 조건에서 자연수라 했기 때문이다.
따라서 x, y, z에 +1을 일단 하나씩은 무조건 나눠줘야한다.
그러면 간단하다.
일단 +1을 하나씩 나눠준다음 하던대로 하면 되는거다.
+1을 하나씩 나눠주면 +1이 4개 남을것이고
따라서 a+b+c=4을 만족시키는 음이 아닌 정수해의 개수를 구하는 문제가 된다.
이는 +1이 a, b, c 중 어디로 갈지 셋중하나를 '선택' 하는 행위를
+1이 4개니까 '4회' 하며
중복선택을 허용하니까
결론적으로 구하고자 하는 경우의 수는

따라서 답은 15이다.
그리고 추가로, 여기서는 간단한 조건을 주었지만
조건이 복잡할 경우엔
문제 상황을 이해한다음 식을 세우려 하면 오히려 실수하기 쉬우니
그냥 하나하나 세는것도 방법이다.
어차피 답만 내면 되는거다.
- 4 : n명에게 같은 종류 m개를 나눠주는 경우 -
사실 세번째 주제와 완전히 똑같은거다.
3명에게 똑같은 사탕 6개를 나눠준다고 해보자.
단, 사탕을 못받는사람이 있을수도 있다.
이때 나눠주는 경우의 수는?
이때 사람들은
어차피 똑같은 사탕이기때문에
사탕끼리는 구별하려들지 않는다.
어차피 다 똑같은맛인데 구별할 방법도 없고 필요도 없는것이다.
즉 사탕의 개수에만 관심이 있다.
그럼 첫번째사람이 받는 사탕의 개수를 a
두번째사람이 받는 사탕의 개수를 b
세번째사람이 받는 사탕의 개수를 c 라 하면
a+b+c = 6 이라는 식이 완성된다.
사탕을 못받는 사람이 있을수도 있으니
a가 0일수도 있다.
따라서 이 문제는
아까 다뤘던
x+y+z+w = 6 을 만족시키는 음이 아닌 정수해 (x, y, z, w)의 순서쌍의 개수는?
이 문제와 사실상 똑같은 문제가 된다.
여기서 다룰건
a+b+c=6 을 만족키시는 음이 아닌 정수해 (a, b, c)의 순서쌍의 개수 를 구할거니까
답은
사탕 입장에서 3명중 한명에게 선택해서 가고
이걸 6번 반복하며 중복선택이 가능하니까

따라서 답은 28
- 요약 -
지금까지 확통에 등장하는 경우의 수를 전부 다뤘다.
바로 다음내용인 이항정리가 남긴 했지만 얘는 경우의수라 하기는 애매하다.
같은것들을 다른것들에게 나눠주는 경우 : 중복조합
- 예제 -

서로 구별되지 않는 공 10개를 A, B, C 3명에게 남김없이 나눠주는데
A가 공을 3개 받는다고 하고
공을 한개도 못받는사람이 있을수 있다고한다.
즉 A가 받는 공의 수를 a
B가 받는 공의 수를 b
C가 받는 공의 수를 c라 하면
a+b+c = 10 인데
문제의 조건에서 a=3 이니까
b+c = 7 이다.
1개의 공도 받지 못하는 사람이 있을수 있으므로
b와 c는 0일수도 있다.
따라서 b+c=7 을 만족하는 음이 아닌 정수해 (b, c) 의 순서쌍의 개수를 구하면 된다.
똑같은걸 벌써 4번째 하고있으므로 자세한 설명은 생략한다.
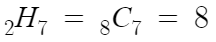
따라서 답은 8
'확률과 통계 > I. 경우의 수' 카테고리의 다른 글
| 이항정리 #2 - 이항계수의 성질과 파스칼의 삼각형 (0) | 2021.12.01 |
|---|---|
| 이항정리 #1 - 이항정리의 뜻과 원리 (0) | 2021.11.29 |
| 중복조합 #1 - 중복조합의 뜻과 계산 원리 (1) | 2021.11.26 |
| 여러가지 순열 #3 - 같은 것이 있는 순열 (0) | 2021.11.26 |
| 여러가지 순열 #2 - 중복순열 (0) | 2021.11.24 |



