
- 들어가며 -
'킬러문제 풀이' 카테고리는
소수의 최고난도 문제들만 모아서 해설해주는 곳입니다.
최근 수능 기조가 킬러 하향, 준킬러 상향으로 바뀌면서
이제는 이정도 난이도의 문제는 보기 어렵습니다.
개념만 뗀 수준이어도 이해하도록 쉽게, 차근차근 풀어드립니다.
스스로 풀어내셨다면 진심으로 축하드립니다.
- 171130 -

답은 216 이다.
조건을 하나씩 풀어보겠다.

g(x)가 사차함수니까
f(x)는 삼차함수인가? 라고 추론해볼수 있다.
물론 이는 비약적인 추론이고, 이 문제에서는 실제로 틀린 추론이다.
하지만 여태 풀어온 문제들로 미루어 봤을 때, 수능 응시자 입장에서
우선 이런 생각이 드는것이 상식적이다.
보통 식이 저런 모양이면 f(x)가 삼차함수였기 때문이다.
일단 f(x)가 삼차함수인가? 하고 풀다가 오류 발견되면 그때 수정하면 되는거다.
우선 f(x)가 삼차함수라 두고 (나) 조건으로 넘어가겠다.

이 조건에 의하면, f(x)는 극댓값이 최소 2개 있다.
f(x)가 삼차함수라면, 극댓값을 하나밖에 갖지 못한다.
따라서 f(x)는 삼차함수가 아니구나. 라는걸 알 수 있다.
그럼 f(x)는 뭐하는 함수인가?
일단 아래 조건을 써보자.

x>a 이기 때문에, x-a ≠ 0 이고
양변을 x-a 로 나눠도 된다.
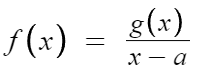
f(x)는, 분모가 x-a 이고 분자가 사차식인 '유리함수'이다.
어떻게 이런생각을 한건지 문제 참 잘만들었다.
아무튼 f(x)는 극대지점이 최소 2개고 그 값은 M 이라는것을 이용하겠다.
극대지점을 찾는 가장 쉬운방법은 미분하는것이다.
미분해서 도함수의 값이 0이면, 거기가 바로 극값을 갖는 지점이다.
조심할건, 이렇게 풀기 전에 f(x)의 미분가능성을 점검해볼 필요가 있다.
미분불가능하면 당연히 이렇게 풀면 안된다.
분자인 g(x)는 다항함수이므로 미분가능,
분모인 x-a도 다항함수이므로 미분가능,
그리고 f(x)의 정의역이 x>a 이므로 분모는 0이 될일이 없음.
위를 근거로, f(x)는 미분가능하다.
따라서 f '(α) = f '(β) = 0 이다.
그리고 f(x)가 x=α, x=β 에서 극댓값 M을 가지므로,
아래와 같은 '방정식'을 세울 수 있다.
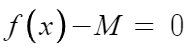
이 방정식의 근은 x=α, x=β 이다.
따라서, 이러한 결론을 얻는다.

따라서, f(x)-M 이라는 식은
(x-α)²(x-β)² 을 인수로 갖는다.
여기까지 따라왔다면 반은 푼거다.
여태까지 한걸 좀 쉽게 정리하면,
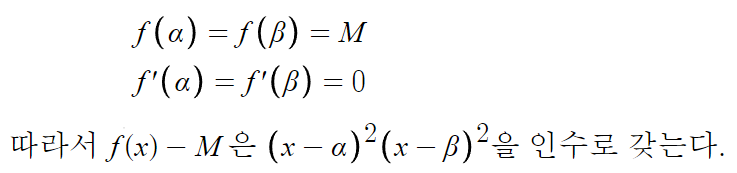
이제 이걸 이용해서 f(x)를 작성할것이다.
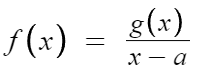
일단 (가)조건에서 얻어낸 이 식에 의하면,
g(x)를 구하면 f(x)를 구할수 있다.
g(x)는 사차함수라는 정보가 있기때문에,
g(x)를 구하는게 더 쉽다.
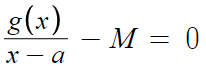
위 식을 아까 구했었다.
그리고 이것이 x=α, x=β 에서 중근을 갖는다는것도 안다.
일단 좀 계산하기 편하게 양변에 x-a를 곱해주자.
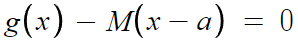
이것이 x=α, x=β 에서 중근을 갖는다.
따라서, g(α)와 g(β)의 값은
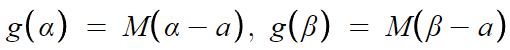
미분하면 g'(α)와 g'(β) 의 값도 알 수 있다.
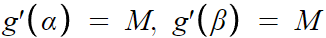
구해진 함숫값들을 토대로,
이러한 결론을 얻는다.
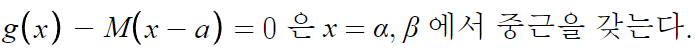
따라서, g(x) - M(x-a) 라는 식은
(x-α)²(x-β)² 을 인수로 갖는다.
그런데, g(x) - M(x-a)는 최고차항의 계수가 -1인 사차식이므로
아래의 관계식을 얻는다.
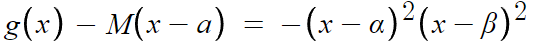
-M(x-a)만 이항해주면 g(x) 추론 끝
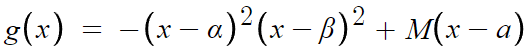
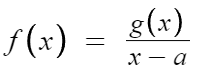
우리는 f(x)를 구하기 위해 g(x)를 구한거니까
대입해서 정리만 해주면 f(x)도 추론 끝
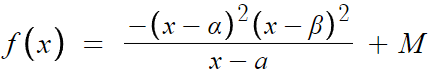
이제 75%정도 왔다.
드디어 (다) 조건을 써먹을 때가 왔다.

좀 쉽게 다시말하자면,
f(x)의 극점의 개수가
g(x)의 극점의 개수보다 많다는거다.
g(x)는 사차함수기 때문에,
g(x)의 극점은 3개 아니면 1개이다.
다음으로 f(x)의 극점의 개수를 세기 위해서는
f(x)를 미분해봐야한다.
f '(x)=0 이면서 f ''(x)≠0 이면 극점인거다.
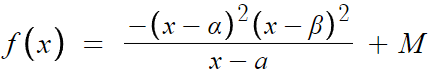
근데 이걸 어느세월에 미분하나. 해보면 엄청나게 더럽게나온다.
생각해서 좀 세련되게 풀어보자는거다.
f(x)를 미분하면 분모는 이차식일거고
분자가 중요한데, 사차식을 일차식으로 나눈걸 미분하는거니까
f '(x) 의 분자는 사차식이다.
따라서 f '(x)의 실근은 많이 나와봐야 최대 4개이다.
따라서 f(x)의 극점은 최대 4개이다.
근데 f(x)의 극점이 4개일순 없다.
f(x)의 분모가 일차식이고, 분자가 사차식이기 때문에,
f(x)의 극점은 무조건 홀수개여야한다.
따라서 f(x)의 극점은 최대 3개이다.
그런데, g(x)의 극점의 개수가 f(x)의 극점의 개수보다 작아야하므로
다음과 같은 결론을 얻는다.
" g(x)의 극점의 개수는 1개이다. "
g(x)의 극점의 개수가 1개인데,
g(x)는 사차함수이므로
g'(x)는 삼차함수이고
따라서 g'(x)=0 은 실근 하나, 중근 하나
혹은 실근 하나, 허근 두개를 갖는다.
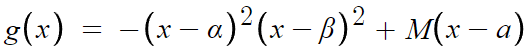
g(x)를 (나)조건 풀면서 추론해놨으니까 이거 미분한다음
얘가 중근 갖거나 허근 가진다고 하면 끝난다.
g(x)를 미분한다.
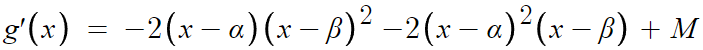
식이 더러우니 정리한다.
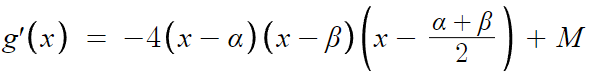
이 g'(x)가 중근을 갖거나, 허근을 갖는다.
즉,
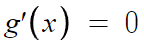
얘가 중근을 갖거나, 허근을 갖는다.
등식의 성질을 이용. 양변에 M을 빼주면,
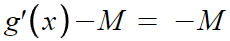
이것도 중근 또는 허근을 가질것이다.
그냥 양변에 똑같이 M 빼준것 뿐이니까

그래서 M은 왜 뺀거냐면,
M을 좌변으로 넘겨버리면
우변의 그래프를 그리고 분석하기가 쉬워져서 그렇다.
우변 식의 그래프를 그리면
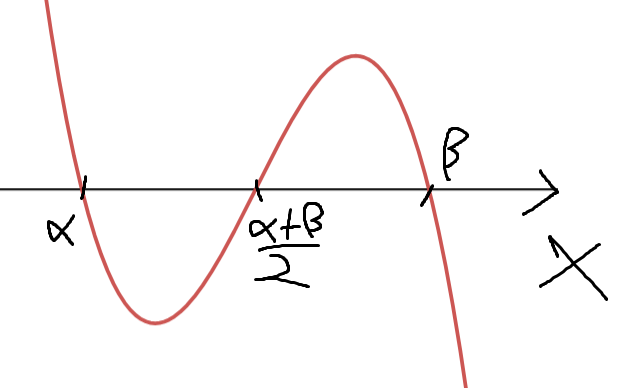
그런데, g'(x)-M = -M 이 중근 또는 허근을 가지므로,
y = -M 의 그래프가 위치할 수 있는곳은
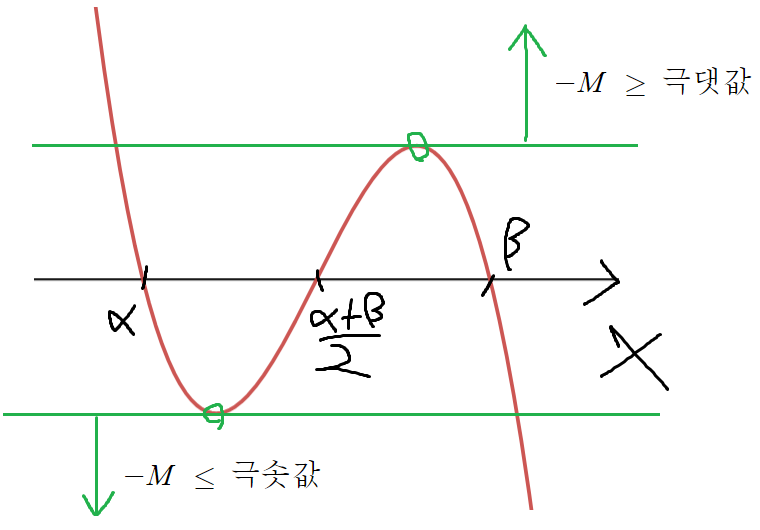
극대지점 이상에 있거나,
극소지점 이하에 있어야한다.
즉,
-M ≥ 극댓값 이거나,
-M ≤ 극솟값 이어야한다.
그런데, -M ≥ 극댓값 인 경우는 존재하지 않는다.
왜냐면,
문제의 조건에서 M>0, 즉 M은 양수이므로.
따라서, y = -M 의 그래프는 x축 아래에 위치한다.
따라서 y = -M 의 그래프가 극대지점 이상에 위치하는건 불가능하다.
즉, -M이 음수기때문에 -M≥극댓값인 경우는 존재하지 않는다.
따라서, -M ≤ 극솟값 이어야한다.
그런데, 문제에서 구하라는건 M의 최솟값이다.
M의 최솟값이라는건
-M이 최대가 되도록 하는 M의 값 말하는거다.
따라서, -M = 극솟값 일때가 M이 최소일 때다.
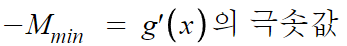
이제 진짜 거의 다왔다. 계산만 하면 된다.
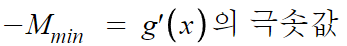
g'(x)의 극솟값을 구하려면 g'(x)를 또 미분해야한다.
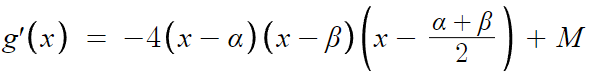
우선 문제에서 제시한 조건에 의하면,

이므로, β = 6√3 + α 이다.
이를 대입해서 식을 다시쓰면,
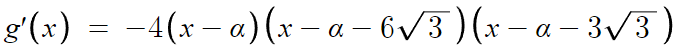
식이 더럽다.
식 단순화를 위해 '평행이동' 을 이용할것이다.
g'(x)는 그냥 삼차함수고, x방향으로 평행이동하는걸로는
극솟값에 아무런 영향을 주지 못한다.
물론 극소지점 자체는 바뀐다.
하지만 그냥 x방향으로만 움직이는거라 극솟값은 바뀌지 않는다.
따라서 g'(x)를 x방향으로 -α-3√3 만큼 평행이동해버리면
식이 아주 간단해진다.
이건 야매가 아니라, 계산을 줄이는 기술이다.
이해가 안되면 그냥 깡으로 계산하시면 된다.
아무튼 평행이동해주면
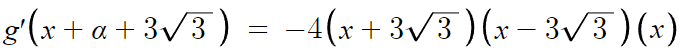
합차공식을 이용해 간단하게 해주면
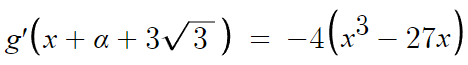
이제 극솟값을 구하기 위해 얘를 미분하면 된다.
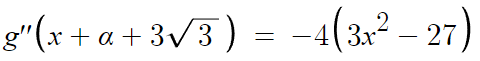
따라서, g'( x+α+3√3 ) 은 x = -3 에서 극소, x = 3 에서 극대이다.
따라서, 극솟값은
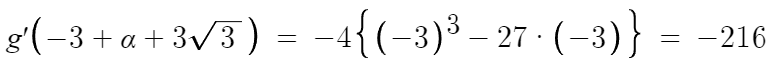
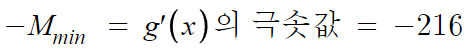
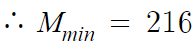
끝.
답은 216