
한글 파일, pdf 파일 첨부하였습니다.
수능날 프린트해가시면 됩니다.
- 수열의 극한 -
수열이 곧 함수이기 때문에
사실상 함수의 극한과 다를게 없는 단원이다.
수학II 하듯이 하면 된다.
- 등비수열의 수렴•발산 -

이게 등비수열의 일반항인데
r > 1 : 크기가 무한히 큰 수로 발산
r = 1 : 첫째항의 값으로 수렴
-1 < r < 1 : 0에 수렴
r ≤ -1 : 발산(진동)
- 급수의 정의와 수렴 조건 -


즉 수열의 합의 극한이다.

- 급수의 성질 -

- 주의 -
1. 곱해지거나 나눠진게 상수가 아니면 막 찢으면 안된다.

2.

얘가 수렴한다고

얘네가 각각 수렴하는건 아니다.
a_n = n 이라 하고
b_n = -n 이라 하면
a_n + b_n = 0 이기 때문에
두 수열의 합의 급수는 수렴하겠지만
각각의 수열의 극한값은 무한대이기 때문에 수렴하지 않는다.
- 등비급수 -
등비수열의 무한합

|r| < 1 이면 등비급수는 수렴한다.
수렴값은 다음과 같다.

- 등비급수의 활용 : 넓이, 길이의 무한합 -
수능 단골 소재인데
푸는 방법은 간단하다.

등비급수 식이 이거니까
첫번째 항의 값 a 와
공비 r 만 알아낸다음 저 식에 대입하면 된다.
- e의 정의 -


핵심은
동그라미친 둘은 서로 역수관계여야한다.

- 자연로그의 정의 -
밑이 자연상수 e인 로그이며 ln이라 쓴다.

- 지수함수의 극한 -



- 로그함수의 극한 -



- e의 정의를 이용한 지수함수와 로그함수의 극한 -
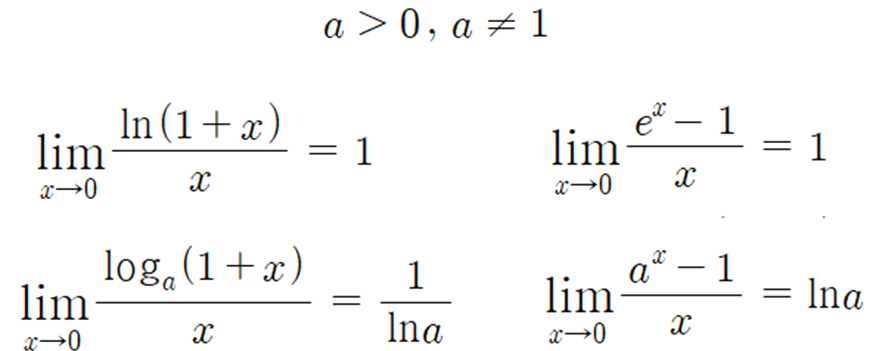
- 지수함수와 로그함수의 미분 -

- 삼각함수 추가개념 -


이 식을 변형하면 아래 식들이 완성된다.


- 삼각함수의 덧셈정리 -



- 삼각함수의 덧셈정리의 활용 : 두 직선이 이루는 예각의 크기 -
기울기가 각각 tanθ₁, tanθ₂ 인 두 직선이 이루는 예각의 크기를 θ라 하면
tanθ를 이용해 나타낼 수 있다.

- 삼각함수의 덧셈정리의 응용 -
삼각함수의 덧셈정리 식에서
β = α 라 하면 아래 식들이 완성된다.



cos²α+sin²α = 1 이므로
-sin²α = cos²α-1 이고
cos(2α) = 2cos²α-1 이나
cos(2α) = 1-2sin²α 으로 한번 더 변형할 수 있다.
이를 한번 더 응용하여
α에 대한 삼각함수의 식 만으로
2α에 대한 삼각함수의 식을 구할 수 있다.



- 삼각함수의 합성 -

이런 함수의 최댓값과 최솟값은
삼각함수의 합성을 이용해서 구한다.


- 삼각함수의 극한과 미분 -





- 여러가지 미분법 공식 -
- 몫의 미분법 -


- 합성함수의 미분법 -

- 로그함수의 도함수 -


로그함수의 진수에 함수가 있을 경우
로그함수의 미분과 합성함수의 미분법을 이용한다.
- 매개변수로 나타내어진 함수의 미분법 -
x와 y를 둘다 t에 대한 식으로 나타낼 수 있는 경우
즉 x = f(t) , y = g(t) 인 경우
dy/dx는 다음과 같다.

- 음함수의 미분법 -
f(x, y) = 0 꼴로 나타내어지는걸 음함수라 한다.
예를 들어 x³ + y - xy² = 0 라고 주어진 음함수에서
dy/dx를 구하고자 한다면
y를 x에 대한 함수로 보고
하던대로 미분하면 된다.

- 함수 y=xⁿ 의 도함수 -


- 역함수의 미분법 -
역함수의 정의와 합성함수의 미분을 이용한다.

g(x)가 f(x)의 역함수라면 위 식이 항등식이므로
양변을 미분하면

- 이계도함수 -
도함수를 미분한게 이계도함수이다.
즉 함수를 두번 미분하면 이계도함수가 된다.

이계도함수가 존재하려면 도함수가 연속이어야 한다.
이계도함수의 4가지 표현법은 다음과 같다.

- 이계도함수의 활용 1 : 극대•극소 판정 -
이계도함수를 가지는 함수 f(x)에 대하여
f'(a)=0 일 때,
f''(a)<0 이면 f(x)는 x=a에서 극대이고,
f''(a)>0 이면 f(x)는 x=a에서 극소이다.
- 이계도함수의 활용 2 : 오목•볼록 판정 -
f''(x)>0 이면 함수 f(x)는 이 구간에서 오목하다.(아래로 볼록하다)
f''(x)<0 이면 함수 f(x)는 이 구간에서 위로 볼록하다.
- 이계도함수의 활용 3 : 변곡점 -
이계도함수를 가지는 함수 f(x)에 대하여
f''(a)=0 이고, x=a의 좌우에서 f''(x)의 부호가 바뀐다면
점 ( a, f(a) ) 는 y=f(x)의 변곡점이다.
- 여러가지 적분법 공식 -
- y = xⁿ 의 부정적분 -

- 지수함수의 부정적분 -


- 삼각함수의 부정적분 -


- 치환적분법 -
말그대로 기존의 변수를 새 변수로 치환해서 적분하는것
예시 : tanx의 적분

주의할 점은
정적분에서 치환적분법을 사용할경우
치환했기때문에 적분구간이 바뀔 수 있다.
- 부분적분법 -
두 함수의 곱을 적분하는 방법

곱의 미분법의 응용이다.
f(x) = 미분하기 쉬운 함수
g'(x) = 적분하기 쉬운 함수
로 두는게 풀기 쉽다.
- 정적분과 급수의 관계 -
정적분의 정의는 다음과 같다.

어떤 함수가 이루는 도형의 넓이를 구할때 급수를 쓰는데
그게 식이 복잡하니까 정적분이라는 이름으로 간단히 표현한것이다.
여기서 급수의 각 부분이 무엇을 의미하는지를 이해하고 있어야한다.

- 입체도형의 부피 -
닫힌 구간 [a, b]에서 x좌표가 x인 점을 지나고
x축에 수직인 평면으로 자른 단면의 넓이가 S(x)인 입체도형의
부피 V는

(단, S(x)는 닫힌구간 [a, b]에서 연속이다.)
- 좌표평면 위를 움직이는 점의 움직인 거리 -
t=a부터 t=b까지 점 P가 움직인 거리는 다음과 같다.

- 곡선의 길이 -
사실 곡선의 길이 = 점 P가 움직인 거리 이다.
점 P가 움직이면서 남기는 자취의 길이라고 보면 된다.
x가 t에 대한 함수이고
y도 t에 대한 함수이면
a≤t≤b 에서 곡선의 길이는 다음과 같다.

y = f(x)꼴로 나타내어진 함수 f(x)에서
a≤x≤b 에서 곡선 y=f(x)의 길이 l은 다음과 같다.

끝