
- 들어가며 -
3월 모의고사는 사실 별로 중요하지 않다.
3월 모의고사가 수능 성적이다 라는건 헛소리이니 무시하면 된다.
그래도 6모 9모를 제외하면 그나마 가장 중요한게 3월 모의고사라서
앞으로는 3월모의고사도 수학은 해설을 할 생각이다.
3월 모의고사의 의미는, 고2까지의 수학을 얼마나 잘하느냐를 측정하는것이다.
즉 3월 모의고사의 성적이 좋지 않다면 고2까지의 수학부터 복습하는것을 추천한다.
그렇게 문제의 근원을 찾아 거슬러 내려가다보면, 중등수학이 부족하다는 결론에 다다를수도 있는데,
그러면 중등수학부터 하면 된다.
고3이 무슨 중등수학이냐? 할수 있는데, 중등수학도 절대로 쉽지않다.
고1 3월 모의고사 범위는 중등수학인데 여러분이 고1 3모 만점 못받는게 그 증거다.
여러분의 고2까지의 수학능력을 측정하는 시험이니 해설을 해주긴 할텐데,
3월모의고사는 별로 중요하지 않으니
6모 9모 수능 해설처럼
빈틈이 전혀 없고 하나하나 친절히 설명해주는 정석중의 정석인 풀이로 하기보단
나만의 테크닉이나 논리적 비약(직관)을 조금 이용할것이다.
그래도 해설지보단 친절하다.
혹시 본인이 못 푼 문제인데
어떻게 푸는건지 궁금해서 이 글을 보는거라면
이 글을 보지 말것.
남이 풀어주는걸로는 실력이 늘지 않는다.
풀긴 풀었는데 풀면서 100%확신하진 못하고 약간 찜찜했거나
다른 풀이도 있을까 해서 찾아보는거라면
매우 환영이다.
원하시는 문제로 바로 가고싶으면
N번 문제로 가고싶다면
N )
이 형태로 검색하시면 됩니다.
예를들어 17번으로 가고싶으면 17 )
16 )
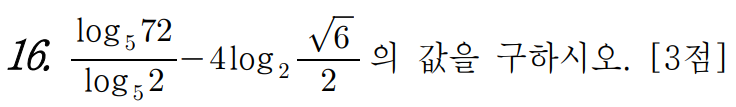
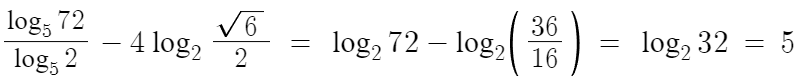
답은 5
17 )

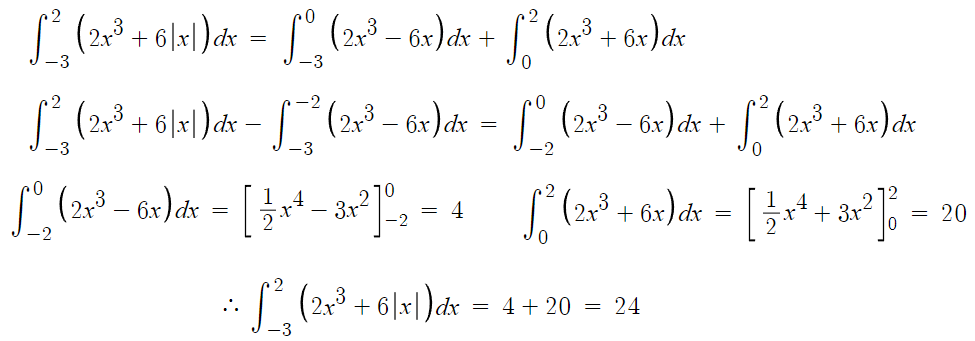
답은 24
18 )
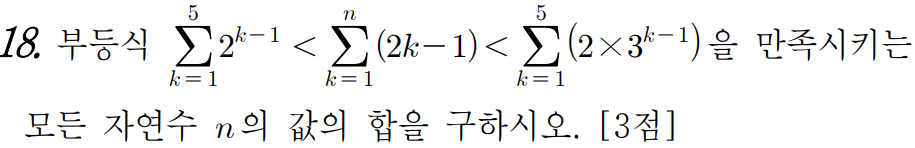

답은 105
19 )

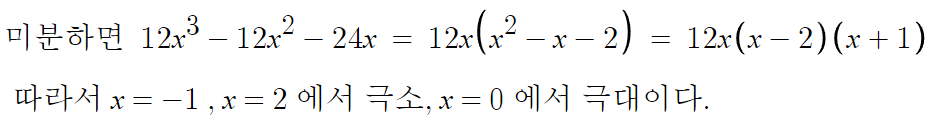
따라서 x=-1과 x=2 에서 저 부등식을 만족하는지만 보면 된다.
둘중 하나는 무조건 저 사차함수의 최솟값이기 때문이다.
하지만 x=-1은 해볼 필요가 없다.
사차함수의 특성에 의하면
극대와 극소 사이의 간격이 더 넓은쪽이 극솟값이 더 작다.
따라서 x=2 에서 주어진 사차함수가 최솟값을 갖는다.
이거 모르면 그냥 x=-1도 대입해보면 돼서 몰라도된다.
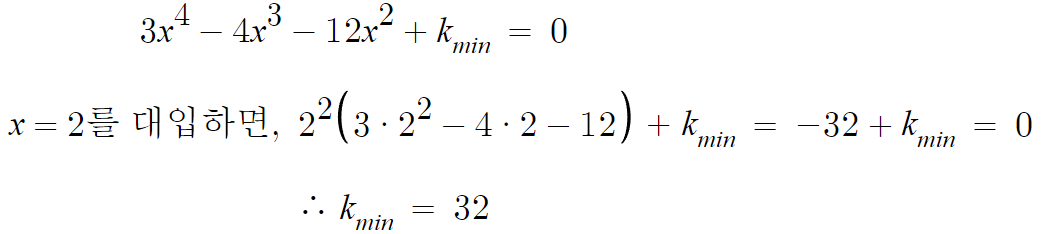
답은 32
20 )

이건 그냥 하나하나 대입하는게 빠르다.


따라서 답은 70
21 )

점 A가 (가)에서 준 곡선 위의 점이라 하므로,
아래 식이 성립한다.
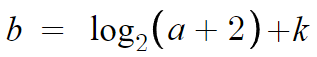
이 식은 keep해둔다.
(나)가 이 문제의 핵심이다.
점 (A)를 직선 y=x에 대하여 대칭이동한 점은
x와 y를 바꾸면 되니까 (b, a) 이다.
따라서 점 (b, a)는 (나)에서 준 곡선 위에 있다.
따라서, 아래 식이 성립한다.
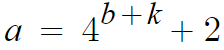
저 두 식을 연립하면 끝난다.
우선 첫번째 식을 정리하자.

이걸
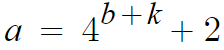
이거랑 연립하면 된다.
위의 식에있는 a에 이걸 대입할거다.
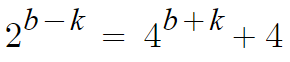
지수가 꼴보기싫은데, 2의 거듭제곱이라는 반복되는 형태가 있으니
치환해서 풀것이다.
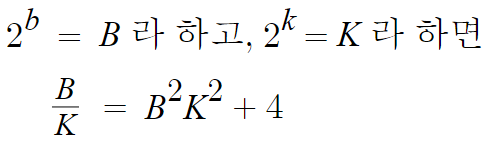
B에 대한 이차방정식이 되었다.
근데 문제 조건에서 이걸 만족시키는 b가 하나밖에 없다고한다.
따라서 이 이차방정식은 중근을 갖는다.
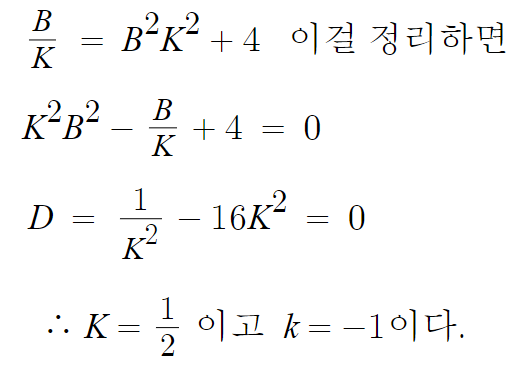
K=1/2 라는걸 저 이차방정식에 대입하면 B를 구할수 있고,
그러면 b도 구할수 있다.
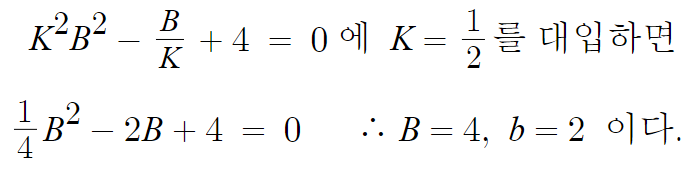
이제 맨 처음에 작성했던 관계식
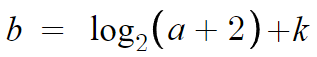
여기다가 b, k 대입만 해주면 끝난다.
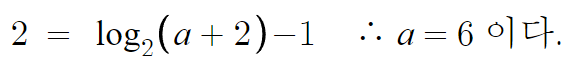
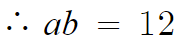
따라서 답은 12
22 )

우선 g(x)는 최고차항의 계수가 1이고 상수항이 0인 삼차함수이므로
g(x)는 x를 인수로 갖는다.
따라서 g(x)를 다음과 같이 쓸 수 있다.
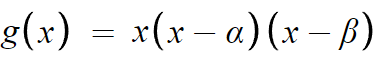
이제 (가) 조건을 보자.
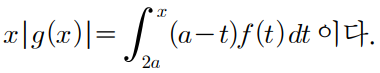
이 식을 보자마자 스쳐지나가는 두가지 생각
1. x=2a 를 대입하면 0이다.
2. 미분하면 적분기호를 뗄수 있다.
x=2a를 대입하면 우변이 0이므로
좌변도 0이어야한다.
따라서 g(2a)=0 이다.
따라서 g(x)는 (x-2a)를 인수로 갖는다.
따라서 g(x)를 다음과 같이 쓸 수 있다.
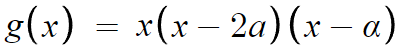
이번엔 양변을 미분해주면
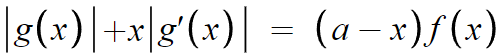
근데, 우리가 아까 얻었던 단서중
g(2a) = 0 이라는게 있다.
|g(x)| + x|g'(x)| 는 삼차함수이므로 x=2a에서 연속이어야한다.
절댓값이 있어서 연속성을 검사해봐야한다.
우선 |g(2a)|=0 이므로 이건 당연히 연속이고
x|g'(x)| 가 x=2a 에서 연속이어야한다.
따라서 g'(2a)=0 이어야한다.
따라서, g(x)는 (x-2a)² 를 인수로 갖고,
g(x)는 다음과 같다.
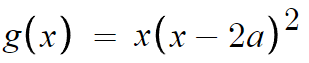
그리고 좌변이 0이므로 우변도 0이고,
따라서 f(x)도 (x-2a)를 인수로 갖는다는것을 알 수 있다.
그리고 x=0 일때도 좌변이 0이므로
f(x)도 x를 인수로 갖는다는것을 알 수 있다.
여기서 주의할것은,
f(x)가 이차식이니 바로 추론끝. 해버리면 안된다.
좌변에 절댓값들이 있으니 f(x)도 범위를 나눠서 생각해봐야될 확률이 높다.
따라서, 그렇게 단정지으면 안된다.
a는 양수인것을 감안하여 g(x)의 개형을 그려보면,
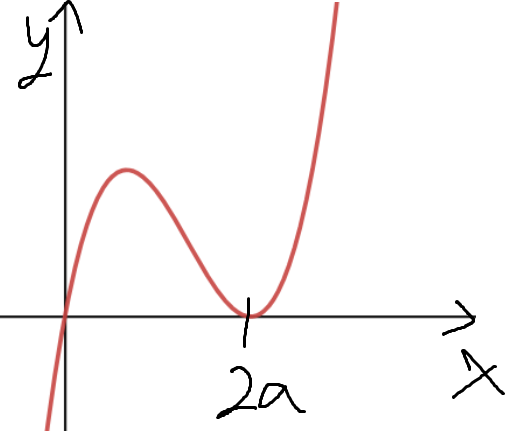
x=2a 에서 접하는 모양으로 그려질것이다.
이제 (나) 조건을 쓸때가 왔다.
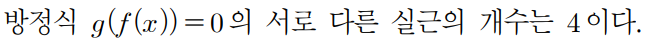
우선 g(x)가 실근을 가지려면 x=0, x=2a 여야 한다.
따라서 g(f(x)) 이 실근을 가지려면
f(x)=0 또는 f(x)=2a 여야하며,
이걸 만족하는 x가 4번 등장해야한다.
f(x)를 정확히 추론하기 위해 문제를 더 뜯어볼 필요가 있다.
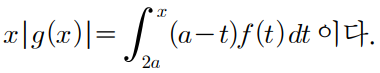
문제에서 준 이 식을 활용해서 f(x)를 추론해볼것이다.
g(x)는 어느정도 추론이 되어있는 상태기 때문에 어렵지 않게 할수있다.
x|g(x)| 는

이렇게 범위를 나눌 수 있으므로

이것도 똑같이 범위를 나눠서 쓸수 있다.
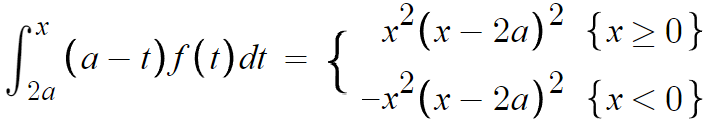
이제 양변을 미분때려버리면 f(x)를 추론할 수 있다.
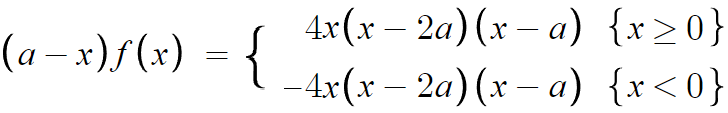
따라서 f(x)는
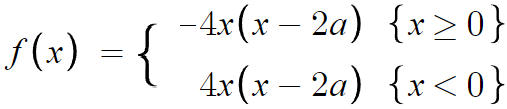
이제 f(x)를 그려보면
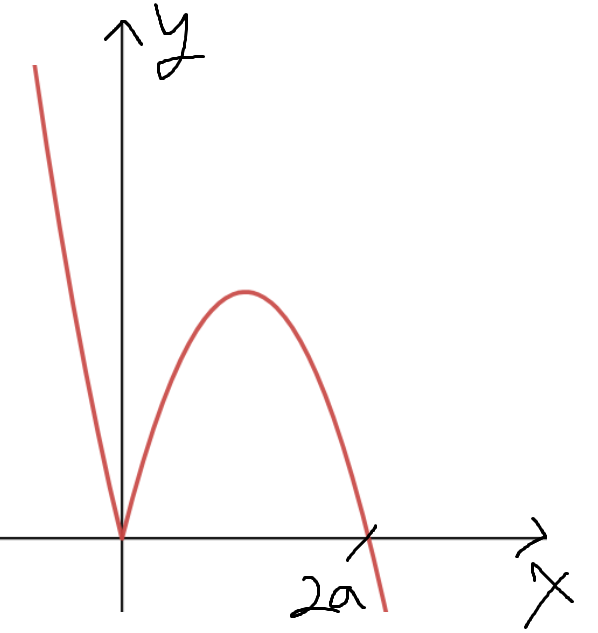
이렇게 생겼다.
여기서 f(x)=0 의 근은 x=0, x=2a 로 두개고
나머지 두개는 f(x)=2a 의 근이다.
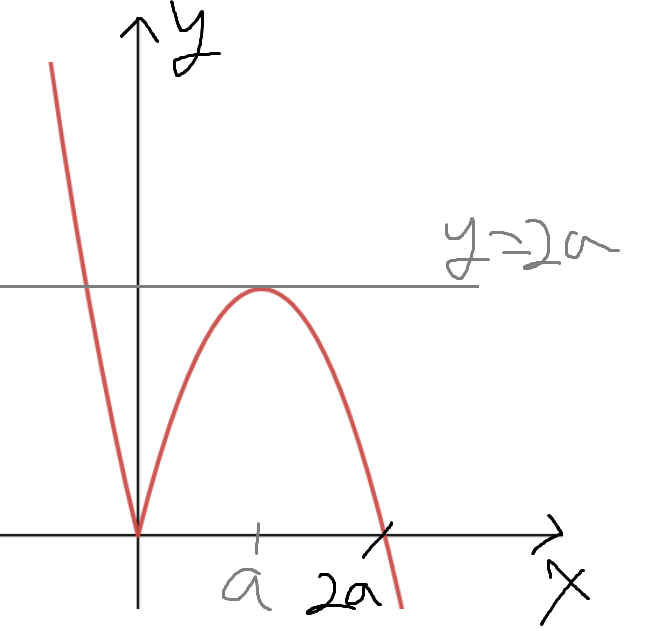
그럼 f(x)의 x>0 에서의 극대점이 (a, 2a) 임을 알수있다.
f(a)=2a 라고 관계식을 쓰면 a가 나온다.
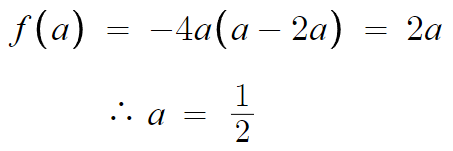
이러면 f(x)의 추론이 완료되었다.
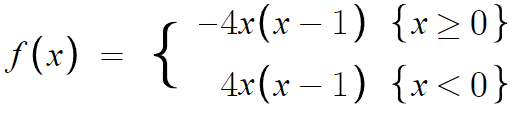

하라는대로 적분만 하면 끝

따라서 답은 4
'2023학년도 기출 해설 > 2022년 3월 학력평가 해설' 카테고리의 다른 글
| 2022년 3월 학력평가 수학 공통 1번~15번 해설 (0) | 2022.04.20 |
|---|
