
- 개요 -
곱의 법칙의 심화과정이다.
곱의 법칙을 소홀히 했다면 여기가 어렵게 느껴질것이다.
- 순열이란? -
한 줄로 요약하자면,
순열 : 뽑아서 나열하는것
정확한 뜻은 이렇다.

n개 중에서 r개를 뽑은 다음,
그 r개를 일렬로 쭉 나열하는 '시행'을 '순열'이라 한다.
n개 '중에서' 뽑는것이므로, r은 n보다 커질 수 없고
하나 이상은 뽑아야 하므로 1보다 작을수도 없다.
그러면 그렇게 나열된 것은
무엇을 뽑느냐, 뽑은 다음 어떤 순서로 나열하느냐 에 따라서
여러가지가 나오게 될 것이다.
즉, 순열은 한두개가 아니다.
이 때, 이러한 순열의 수를 기호로 ₙPᵣ 로 나타낸다.
쉽게 말해서 ₙPᵣ은 '순열의 경우의 수' 이다.
추가로, 기호로 P를 쓰는 이유는
순열이 영어로 Permutation 이라서 앞 글자 따온것이다.
- 순열의 수 기본 계산법 -
직접 간단한 것부터 해보겠다.

이걸 구해보겠다.
저것의 뜻은,
서로 다른 5개 중 3개를 뽑아서
그 3개를 일렬로 나열하는 방법의 수
즉, 순열의 수
이 문제에서 준 순열 = '5개중 3개를 뽑아서 나열한다'는 '시행'
따라서, 5개중 3개를 뽑아서 나열하는 경우의 수를 구해야한다.
어떤 식으로 할거냐면,
하나 뽑아서 나열하고
그다음 하나 뽑아서 나열하고
마지막으로 하나 뽑아서 나열하고
이런 식으로 진행할것이다.

이해를 돕기 위해 예시를 가져오겠다.
뽑을 것 5개(알파벳 A, B, C, D, E) 가 있고
3개 뽑혀서 나열될 자리 3자리가 있다.
이 3자리에 알파벳 3개를 뽑아서 전부 채워넣는것 까지가
'1회의 시행' 이며, '순열'이다.

첫 번째 자리부터 채워보자.
첫 번째 자리에 올 수 있는 알파벳은 5개이며,
따라서 '첫번째 자리에 알파벳을 뽑아서 나열'
하는 경우의 수는 5 이다.

이번엔 두 번째 자리를 채워보자.
첫 번째 자리에 어떤 알파벳이 뽑혀 들어갔을테니,
이제 남은 알파벳은 4개이다.
따라서 '두번째 자리에 알파벳을 뽑아서 나열'
하는 경우의 수는 4 이다.
Q) 어떻게 첫번째자리와 두번째자리의 경우의 수가 다를 수 있나요?
첫 번째 자리에 알파벳을 '채운 후'에 두 번째 자리를 이어서 채우는거기 때문이다.
그래서 이 둘은 다른 사건이고, 경우의 수가 다르게 나온다.
만약 두번째 자리를 가장 먼저 채우기로 했다면,
두번째 자리의 경우의 수는 5, 첫번째 자리의 경우의 수는 4가 될것이다.

마지막으로 세 번째 자리를 채워보자.
첫번째, 두번째 자리에 어떤 알파벳 2개가 뽑혀 들어갔을테니
이제 남은 알파벡은 3개이다.
따라서 '세번째 자리에 알파벳을 뽑아서 나열'
하는 경우의 수는 3 이다.
정리하자면,

5개중 3개를 뽑아서 나열하는 경우의 수는
첫 번째 자리에 나열하는 경우의 수 5
두 번째 자리에 나열하는 경우의 수 4
세 번째 자리에 나열하는 경우의 수 3
이제 이 셋을 적당히 계산하면 되는데,
'3개를 뽑아서 나열한다'라는 '1회의 시행'에서
각각의 자리에 나열한다는 저 사건들은 같이 일어날 수 있는가?
그렇다. 3개의 자리에 모두 다 나열하는것 까지가 1회의 시행이기 때문이다.
즉, 1회의 시행에서 '첫번째 자리에 나열', '두번째 자리에 나열',
'세번째 자리에 나열' 이 3개의 사건이 전부 일어나야 한다.
따라서, 각각의 자리에 나열하는 경우의 수를
곱의 법칙을 적용해서, 전부 곱해주면 된다.

따라서, 5개중 3개를 뽑아서 나열하는 경우의 수는
(첫 번째 자리에 나열하는 경우의수)
×
(두 번째 자리에 나열하는 경우의수)
×
(세 번째 자리에 나열하는 경우의수)
=
5 × 4 × 3 = 60
따라서 답은 60 이다.

- 순열의 수의 일반화(공식) -

이걸 구해보자.
서로 다른 n개 중 r 개를 뽑아서 나열하는 경우의 수는?
아까와 똑같은 방법으로 간다.

알파벳이 n개, 자리가 r개 있는 상태이다.
이것도 자리를 하나씩 채워볼건데,
몇 개 해보면 나름의 규칙이 있음을 어렵지 않게 찾을 수 있다.
- 첫 번째 자리 -

자리에 들어갈 알파벳이 n개 있으니
첫 번째 자리에 알파벳을 나열하는 경우의 수는 n 이다.
- 두 번째 자리 -

자리에 들어갈 알파벳은 n-1개 있다.
따라서 두 번째 자리에 알파벳을 나열하는 경우의 수는 n-1 이다.
- 세 번째 자리 -

자리에 들어갈 알파벳은 n-2 개 있다.
따라서 세 번째 자리에 알파벳을 나열하는 경우의 수는 n-2 이다.
규칙이 보이는거같으니 이제 조금 일반화 해보자.
- k 번째 자리 -

k 번째 자리를 채우기 전까지
k-1 번째 자리까지 알파벳을 채우고 와야 하므로
최종적으로 k번째 자리에 나열할 수 있는 알파벳은
n에서 k-1 을 뺀 n-k+1 개 이다.
따라서, k 번째 자리에 알파벳을 나열하는 경우의 수는
n-k+1 이다.
- 종합 -

k번째 자리에서의 경우의수가 n-k+1 였다.
자리는 1번째 자리부터 r번째 자리까지 있으므로
k값을 1부터 r까지 하나씩 증가시키며
n-k+1 의 값을 전부 곱해주면 된다.(곱의법칙)

n-1+1=n, n-2+1=n+1, n-3+1=n-2, ... 이므로
잔계산 마무리해주면,
이런 공식을 얻는다.

철저히 '곱의 법칙'만 가지고 얻어낸 결과이다.
어떻게 이런 공식이 나왔으며, 왜 곱의 법칙을 써야하는건지
설명할 수 있어야 고난도 문제들을 무리없이 풀어낼 수 있다.
- 식조작의 재료 : 계승(팩토리얼) -

이건 '경우의 수'를 다룰 때 자주 나오며,
고3 수학에서도 심심치 않게 등장하기 때문에 알아두자.
n! 은 n의 계승 또는 n 팩토리얼(factorial)이라 읽는다.
예시를 들자면,
3! = 1에서 3까지의 모든 자연수의 곱 = 3×2×1 = 6
6! = 1에서 8까지의 모든 자연수의 곱 = 6×5×4×3×2×1 = 720
참고로, 0의 계승(0!) 은 1로 취급한다.

- 순열의 수의 성질 -
1. 서로 다른 n개 중 n개를 뽑아 나열하는 경우의 수는 n! 이다.


순열의 수 공식에서 r 자리에 n을 대입해보면,
결국 1부터 n까지의 모든 자연수의 곱이 되는 것을 볼 수 있으며,
1부터 n까지의 모든 자연수의 곱은 n! 이므로, 식을 간단히 하면

이런 결론을 얻게 되는것이다.
상식적으로 생각해 봐도 그렇다.
n개의 자리가 있고, 뽑을게 n개가 있으니
첫번째 자리 경우의수 n
두번째 자리 경우의수 n-1
k번째 자리 경우의수 n-k+1
...
n번째 자리 경우의수 n-n+1 = 1
이것들을 전부 곱하니, 1부터 n까지의 모든 자연수의 곱 이 된다.
2. 0개를 뽑아 나열하는 경우의 수는 1 이다.

이건 상식적으로 매우 당연한데,
0개를 뽑는다는 건, 아무것도 하지 말라는것
아무것도 안한다는것 자체가 하나의 사건이므로
경우의 수는 결국 1이 되는것이다.
3. 계승을 이용해 순열 공식을 간단히 하기


계승(팩토리얼)을 이용하면, 이 공식을 더 간단히 할 수 있다.

n-r+1 부터 n까지 모든 자연수의 곱을 구한다 치면,
1 부터 n 까지 모든 자연수의 곱을 계산한 뒤,
그걸 1부터 n-r 까지 모든 자연수의 곱으로 나눠주면 된다.
그럼 1부터 n-r 까지의 곱은 전부 약분되면서
결론적으로 n-r+1 부터 n까지의 곱 만 남게된다.
이해를 돕기 위해, 처음에 풀었던 문제를 예시로 들어보겠다.

n=5, r=3 이니까 대입해주면

- 예제 -
하기 전에 읽을것 :
공식이 있긴 하지만, 불안하거나 헷갈린다 싶으면
그냥 하던대로 곱의법칙을 이용해 구하는것도 좋은 방법이다.
'경우의 수' 문제를 잘 푸는 방법은
'공식에 너무 의존하지 않는 것' 이다.
1 )

천천히 하나씩 구해보자.
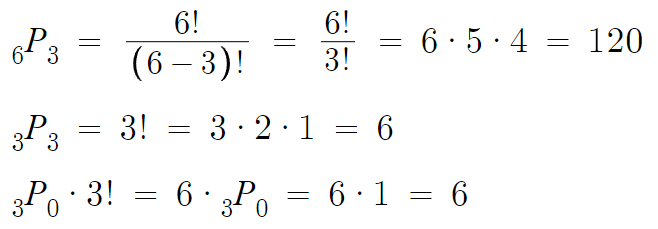
이제 마무리계산 해주면,
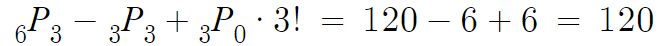
따라서 답은 120
2 )

그냥 공식에 대입해서 만족하는 k값 찾으면 되는거다.
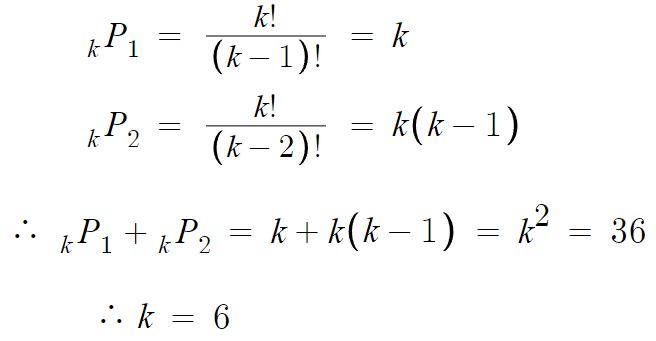
따라서 답은 6
3 )

1 )
방법의 수 = 경우의 수
네 개의 문자를 모두 사용하여 일렬로 나열하라는건,
네 개의 자리에 네 개의 알파벳을 나열하라는 뜻이다.
따라서, 이건 순열의 수를 묻는 문제이다.
뽑을 수 있는 문자는 총 4개
뽑아서 나열할 자리도 총 4개
따라서, 이 때 경우의 수는
₄P₄ = 4! = 24
따라서 답은 24
2 )
A가 맨 마지막에 오도록 하라는건,
일단 A는 4번째 자리에 가야만 한다는 뜻이다.
이러면 오히려 쉬운 상황이 되는데,
그림으로 나타내자면 이렇게 된거다.
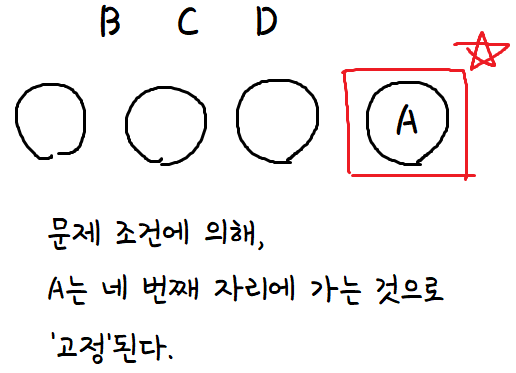
따라서, 남은 3개의 알파벳을
남은 3개의 자리에 그냥 나열해주면 된다.
그런 경우의 수는 ₃P₃ = 3! = 6
따라서 답은 6
'수학(하) > III. 순열과 조합' 카테고리의 다른 글
| 조합 #1 - 조합이란? (0) | 2022.10.09 |
|---|---|
| 순열 #2 - 순열 문제풀이 (0) | 2022.08.28 |
| 경우의 수 : 합의 법칙과 곱의 법칙 (0) | 2022.08.20 |


