
- 표준화의 필요성 -

정규분포가 뭔지는 알았고 쓰는법도 조금 알았는데
아직 뭔가 부족하다.
왜인지 천천히 설명해보겠다.
지금부터 확률변수 X의 값을 변화시켜보겠다.
우선 위의 정규분포에서
평균이 10, 표준편차가 2 라고 해보자.
즉 X는 정규분포 N(10, 2²) 를 따른다.

여기서 핵심은
X값을 아무리 변화시켜도
m과 σ는 변하지 않는다.
변하는건 σ 앞에 붙어있는 숫자
즉 σ의 계수 뿐이다.
따라서 X값을 나타낼 때 m과 σ를 매번 써주는건 비효율적이다.
평균값에서 얼마나 떨어져있는지만 알면 되는거다.
즉 X가 m+kσ 형태니까
k값만 알면 되는거다.
그니까 k값만 가지고도 X값이 표현되니까
일일이 m, σ 적고있지 말고 간단하게 쓰자 이거다.
따라서 이때 해주는게 '표준화'이다.
- 표준화 -
X값은 m+0.5σ, m+σ, m+1.5σ 와 같이 될텐데
여기서 σ의 계수인 0.5, 1, 1.5 만 떼어내는 과정이다.
떼어내는 방법은 간단하다.
m을 뺀다음 σ로 나누면 k만 남는다.

X를 k로 바꾼것
따라서 k값은 더이상 X가 아니다.
여기서 k값을 확률변수 Z라 쓰기로 '약속'한다.
확률변수는 맞는데 X는 아니니까 Z라고 쓰겠다는 의미이다.
따라서 이걸 그대로 그래프를 다시쓰면

이런식으로 k에 대한 그래프로 바뀌며
아주 간단하게 0, 1, 2 와 같이 된다.
이게 표준화 한것이다.
요약하자면
확률변수를 σ의 계수인 Z로 바꾸는 과정을
'표준화' 라고 한다.
여기서 Z를 '표준화된 확률변수' 라고 하고
표준화된 확률변수 Z도 정규분포를 따르니까
표준화된 확률변수 Z가 따르는 정규분포를 '표준정규분포' 라고 한다.
여기서 표준화된 확률변수 Z가 따르는 정규분포를 기호로 표현해보자.
N( 평균, 표준편차² ) 와 같이 될텐데
여기서 핵심은
'정규분포는 평균을 중심으로 좌우대칭'
따라서 Z의 평균은 0이다.
Z값의 의미는 m+kσ에서 k값 임을 잊지 말자.
X의 표준편차는 σ이다.
따라서 Z의 표준편차는 σ의 계수인 1이다.
따라서 Z는 정규분포 N(0, 1²) 을 따른다.
- 예제 -
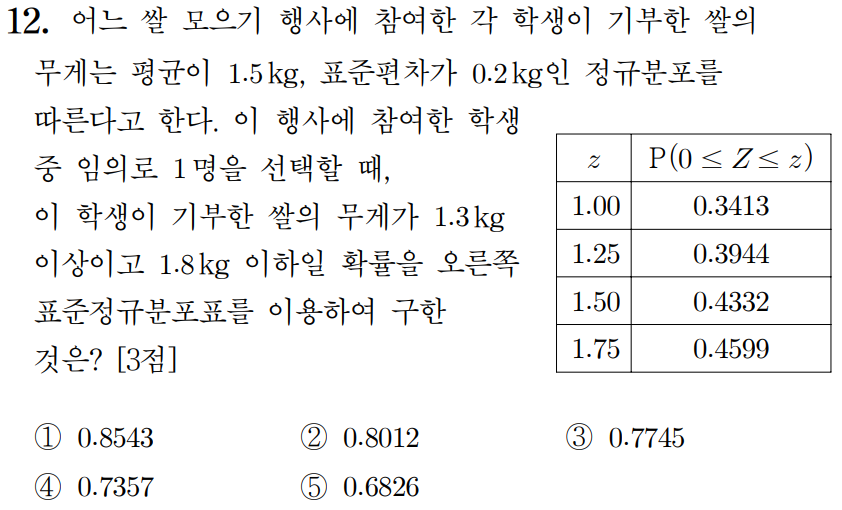
정규분포 문제인데, 확률변수가 Z이다.
따라서 정규분표의 표준화 문제이다.
근데 문제는 쌀의 무게를 분석해야한다는 것이다.
쌀의 무게가 정규분포를 따른다고 했으니
쌀의 무게가 확률변수 X이다.
따라서 X는 정규분포 N(1.5, 0.2²) 로 표현된다.
따라서 기부한 쌀의 무게가 1.3kg 이상이고 1.8kg 이하일 확률은
P( 1.3≤X≤1.8 ) 이다.
하지만 주어진건 표준정규분포표이다.
따라서 표준화를 해줘야한다.
1.3은 1.5-0.2 이므로 m-σ 이다.
1.8은 1.5+0.3 이므로 m+1.5σ 이다.
따라서 X=1.3 을 표준화하면 Z=-1 이고
X=1.8 을 표준화하면 Z=1.5 이다.
따라서 P( 1.3≤X≤1.8 ) = P( -1≤Z≤1.5 )
이제 오른쪽의 표준정규분포표를 이용해 계산만 하면 된다.
P( -1≤Z≤1.5 ) = P( 0≤Z≤1 ) + P( 0≤Z≤1.5 ) = 0.3413 + 0.4332 = 0.7745
따라서 답은 3번
'확률과 통계 > III. 통계' 카테고리의 다른 글
| 통계적 추정 #1 - 표본평균의 평균, 분산, 표준편차 (0) | 2021.12.20 |
|---|---|
| 확률분포 #5 - 정규분포와 이항분포의 관계 (0) | 2021.12.17 |
| 확률분포 #3 - 정규분포의 정의 (0) | 2021.12.17 |
| 연속확률분포와 확률밀도함수 (0) | 2021.12.16 |
| 확률분포 #2 - 이항분포 (0) | 2021.12.14 |



