
- 개요 : 표본조사의 필요성 -
'한국사람의 키의 평균'을 구하고싶으면
현재 한국 인구 5천만명이 넘는 사람의 키를
전부 조사해야한다.
이는 너무 비효율적이며
코로나 백신처럼 국가적인 도움이 없다면
사실상 불가능한 방법이다.
따라서 우리가 할수 있는 방법은
적당히 지나가는 100명정도를 잡아서 키를 조사한다음
그것을 분석하고
그 분석된것을 토대로 전체 평균을 '추정' 하는 방법이다.
즉 '전체 집단'을 조사하기엔 너무 수가 많으니
전체 집단을 조사하는게 아니라
일부를 '추출'해서 그 추출된 '표본'을 조사한다음 이걸로 '추정' 하는것이다.
그래서 이 단원의 이름이 '통계적 추정' 인 것이다.
- 여러가지 용어 -
바로 위에서 예로 들었던것을 그대로 가져와보겠다.
조사하고자 하는것 : 한국 사람의 키의 평균
여기서 조사의 대상이 되는것은 무엇인가?
한국사람이다.
여기서 조사의 대상이 되는 집단,
그리고 그 집단 전체를 '모집단' 이라고 한다.
모집단의 모는 어미 모(母) 이다.
즉 여기서 모집단은 한국사람 전체이다.
모집단 : 조사의 대상이 되는 집단 전체
그리고 아까도 말했듯이
모집단을 다 조사하는건 무리다.
따라서 표본을 적당히 선택해서 그걸 조사해야한다.
그 표본은 당연히 한국사람중에 선택해야한다.
즉 표본은 모집단중에 선택되어야한다.
표본 : 조사를 하기 위해 모집단에서 뽑은 일부분 또는 추출한 자료
그리고 여기서는 표본으로 한국사람 100명을 뽑았으니
표본의 크기는 100이다.
표본의 크기 : 추출한 자료(표본)의 개수
그리고 표본을 추출하는 방법도 두가지정도가 있다.
임의추출 : 그냥 아무조건없이 아무거나 뽑는것
그냥 아무생각없이 아무나 100명 잡아서 키 물어봤으면
그게 임의추출 한것이다.
만약 어린이집에서 100명을 뽑으면
키가 너무 작게 조사될것이고
농구장에서 100명을 뽑으면
키가 너무 크게 조사될것이다.
따라서 이런건 임의추출이 아니다.
복원추출 : 아무거나 뽑긴 하는데
뽑혔던사람이 또 뽑힐수도 있음.
예를 들어, 100명을 조사하는데 A라는 사람이 3번 뽑힐수도 있는거다.
근데 5000만명중에 100명뽑는데
한번 뽑혔던사람이 또 뽑힐 가능성은 거의 없다.
따라서 모집단의 크기가 꽤 크다면, 복원추출이나 임의추출이나 사실상 별 차이가 없다.
근데 100명 뽑아서 구한 평균이 진짜 한국사람 키의 평균인가?
그건 아닐것이다.
즉 100명 뽑아서 구한 평균은
우리가 구하고자하는 한국사람 키의 평균이 아니다.
여기서 우리가 구하고자 하는
한국사람 키의 평균은
모집단의 평균이니까 '모평균' 이라고 한다.
같은 방법으로, 모집단의 분산은 '모분산'
모집단의 표준편차는 '모표준편차' 라고 한다.
그리고 우리가 100명 뽑아서 구한 평균은
표본의 평균이니까 '표본평균' 이라고 한다.
같은 방법으로, 표본집단의 분산은 '표본분산'
표본집단의 표준편차는 '표본표준편차'
- 표본평균 ≠ 모평균 이면 구하는 의미가 없지 않을까? -
100명을 뽑아서 구한 첫번째 표본평균 자체는 큰 의미가 없다.
근데 5000만명중에 100명을 뽑는 경우의 수가 엄청나게 많지 않을까?
즉 '표본평균' 이라는 값은
'표본을 어떻게 뽑느냐'에 따라 달라지는 값이다.
따라서 표본평균은 변수이고,
표본은 완전히 랜덤하게 뽑는거니까 확률변수이다.
즉, 표본평균도 확률변수이다.
이를 X라 표현하면
모집단의 확률변수 X와 겹치니까
X대신 다르게 표현한다.

X bar(엑스 바) 라고 읽는다.
그래서 표본평균을 왜 구하는거냐면
표본평균의 평균은 모평균과 같다.
말이 막 비슷한게 반복돼서 헷갈릴텐데
수많은 표본평균들의 평균을 구하면
결국 모평균과 똑같아진다는 말이다.

증명은 고등학교 수학에서 다루지 않는다.
증명을 보여줄순 있는데 몰라도 된다. 궁금하면 보자.
그리고 엄밀한 증명은 아니지만, 직관적인 이해를 도울만한 예시가 있긴 하다.
집합 {1, 2, 3, ... , 100} 이 있다고 해보자.
이 집합의 원소 값의 평균을 구해볼것이다.
다 더하면 5050이고, 원소가 100개이니 5050/100 = 50.5
따라서 이 집합의 원소 값의 평균은 50.5이다.
따라서 원소 값의 총합은 50.5×100 = (모평균)×(변량의개수)
즉 모평균이 50.5이고 크기가 100인 집단이다.
근데 여기서 표본을 뽑아보자. 부분집합을 뽑아보자는 말이다.
이 집합의 부분집합 중 원소가 두개인 것의 개수는?
원소 100개중 2개 뽑으면 되니 100C2 = 4950 이다.
그리고 이 부분집합에 대한 평균이 바로 표본평균인데,
그럼 이렇게 뽑힌 4950개의 부분집합의 평균이 바로 표본평균의 평균이 되는것이다.
그럼 이 부분집합들의 원소를 전부 더한 값은?
이걸 직접 더할건가? 4950개나 되는데?
곱셈을 활용할것이다.
원소의 개수가 두개면서 1이 포함된 부분집합은 몇개인가?
2와 100중 하나 뽑으면 되니 99개이다.
2가 포함된 부분집합도 같은 논리로 99개이다.
따라서 N이 포함된 부분집합의 개수는 99개이다.
따라서 부분집합들의 원소를 전부 더할거면
1이 99개, 2가 99개, ... 100이 99개 있으므로
1×99 + 2×99 + 3×99 + ... + 100×99 한다음
{1, 2}와 {2, 1}은 같은 집합인데 중복해서 더했으므로 2로 나눠주면
최종적으로 원소의 개수가 두개인 부분집합의 원소의 총합
즉 모든 표본집단의 원소의 총합은
( 1×99 + 2×99 + 3×99 + ... + 100×99 ) / 2 이다.
99가 공통인수이므로 밖으로 빼내면
99 × (1+2+3+...+100) / 2 이다.
근데 1+2+3+...+100의 값은
50.5×100 즉 (모평균)×(모집단의 변량의개수) 이다.
따라서 원소의 개수가 두개인 부분집합의 원소의 총합
즉 모든 표본집단의 원소의 총합은
99 × (모평균) × (모집단의 변량의개수) / 2
이 부분집합의 원소의 합의 평균이 바로 표본평균의 평균이다.
평균 = 총합 / 변량의개수
따라서 표본평균의 평균 = (표본평균의 총합 즉 부분집합의 원소의 총합) / 표본의 개수(부분집합의 개수)
따라서 표본평균의 평균은, (원소의 총합) / 4950 이다.
근데 원소의 총합 = 99 × (모평균) × (모집단의 변량의개수) / 2 이므로
대입해서 정리하면
표본평균의 평균 = (모평균) × (모집단의 변량의개수) / 100
근데 모집단의 변량의 개수가 100이다.
따라서 표본평균의 평균 = 모평균이다.
- 표본평균의 분산과 표준편차 -
표본평균의 평균을 구했으니
이번엔 표본평균의 분산과 표준편차도 알 차례이다.
근데 암기해야된다.
증명을 고등학교수학에서 다루지 않으며,
너무 복잡해서 적어줄수도 없다.

표본평균의 분산 = (모분산) / (표본의 크기)

표본평균의 표준편차 = (모표준편차) / √(표본의 크기)
그리고, 모집단이 정규분포를 따르면, 표본평균도 정규분포를 따른다.

그냥 그렇게 알려져있고, 고등수학 수준에서 증명 불가능하니까 외우자.
- 예제 -

핵심 : 표본평균의 평균은 모평균이다.
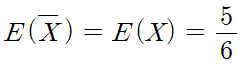
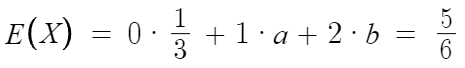
따라서 a+2b = 5/6 이고 답은 5번
'확률과 통계 > III. 통계' 카테고리의 다른 글
| 통계적 추정 #3 - 모평균의 추정과 신뢰도 (0) | 2021.12.23 |
|---|---|
| 통계적 추정 #2 - 표본평균의 분포와 표준화 (0) | 2021.12.20 |
| 확률분포 #5 - 정규분포와 이항분포의 관계 (0) | 2021.12.17 |
| 확률분포 #4 - 정규분포의 표준화 (0) | 2021.12.17 |
| 확률분포 #3 - 정규분포의 정의 (0) | 2021.12.17 |




