
여기는 사실상 대부분의 내용이
그냥 그렇게 알려져 있습니다. 증명은 고등학교과정이 아닙니다.
그냥 외우십시오. 하는 식이기 때문에
사실상 암기하는 부분이다.
확통, 특히 통계는 수학치고 암기할게 좀 많다.
- 정규분포와 이항분포의 관계 -
주제 자체가 좀 의아할것이다.
이항분포는 '이산확률분포'이고
정규분포는 '연속확률분포'이다.
한 번의 시행에서 사건 A가 일어날 확률을 p라고 하고,
일어나지 않을 확률을 q라고 하겠다.
각각의 시행은 독립시행이고, 이 시행을 n번 반복하면
여기서 사건 A가 일어나는 횟수가 바로 이항분포에서의 확률변수 X이다.
여기까진 복습이다.
근데 이 확률변수 X는
이항분포에서 시행 횟수인 n이 충분히 커지면,
근사적으로 정규분포를 따른다.
증명은 아까도 말했듯 고등수학 수준이 아니며,
이항분포의 E(X) = np 증명보다 아주 길고 복잡하기 때문에
다루지 않겠다.
이 부분은 나중에 여유가 되면 따로 다루도록 하겠다.
n이 충분히 커진다는 말은 어렵게 받아들이지 말고
그냥 한 100번 1000번 시행했다면서 문제에 나왔으면
'이항분포인데 시행횟수 많으니까 정규분포를 따르게 되겠구나
따라서 정규분포문제처럼 풀면 되는구나'
라고 생각하고 풀면 된다.
어차피 암기해야되는 부분이라 이정도 수준으로밖에 못낸다.
- 그래서 어떻게 정규분포로 바꾸는가? -
X가 정규분포를 따르므로, N(m, σ²) 형식으로 표현해야하는데,
X가 이항분포를 따르니까
m = E(X) = np
σ² = V(X) = npq
따라서 정리하자면
n이 충분히 크다면 X는 정규분포를 따르며,
N(np, npq) 또는 N(np, (√npq)² )로 표현할수 있다.
- 정규분포로 근사된 이항분포의 표준화 -
하던대로 하면 된다.

물론 여기서도 표준화된 확률변수 Z는
표준정규분포 N(0, 1²) 을 따른다.
- 예제 -
뭔가 쓰다보니 벌써 예제인데
성의없는게 아니라 진짜 내용이 이것밖에 없다.
게다가 암기해야되는 내용이라서
적어놓고는 이렇다 라고 알려주는수밖에 없다.

각각의 시행은 독립시행인데
사건 A가 일어나는 '횟수'를 분석하라고 한다.
따라서 이항분포 문제이다.
여기서 사건 A가 일어나는 횟수가 확률변수 X이다.
확률변수 X는 이항분포를 따른다.
근데 시행 횟수가 1200번이다.
따라서 정규분포로 근사할수 있다.
즉 확률변수 X는 정규분포를 따른다.
N(np, npq) 로 표현할수 있다.
n = 1200
p = 상자 두개 던졌을때 나오는 두 눈의 수의 곱이 홀수일 확률
두 눈의 수의 곱이 홀수려면
상자 두개가 둘다 홀수가 나와야한다.
상자에서 홀수가 나올 확률은 1/2 인데
둘다 홀수 나와야 하니까 p = 1/2 × 1/2 = 1/4
따라서 q = 1 - 1/4 = 3/4
따라서 np = 1200 × 1/4 = 300
npq = 300 × 3/4 = 225 = 15²
따라서 N(np, npq) = N(300, 15²)
따라서 정리하자면,
확률변수 X는 정규분포 N(300, 15²) 을 따른다.
이제 P(X≤270) 을 구하면 되는데
주어진 표가 표준정규분포표이다.
따라서 X를 표준화시켜야한다.
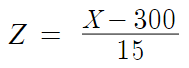
X=270 일때 Z=-2 이기 때문에
P(X≤270)은 P(Z≤-2) 로 표준화된다.
P(Z≤-2)를 구하면 되는것이다.
P(Z≤-2) = P(Z≥2) = P(0≤Z) - P(0≤Z≤2) = 0.5 - 0.477 = 0.023
따라서 p=0.023 이고
따라서 1000p = 23
따라서 답은 23
'확률과 통계 > III. 통계' 카테고리의 다른 글
| 통계적 추정 #2 - 표본평균의 분포와 표준화 (0) | 2021.12.20 |
|---|---|
| 통계적 추정 #1 - 표본평균의 평균, 분산, 표준편차 (0) | 2021.12.20 |
| 확률분포 #4 - 정규분포의 표준화 (0) | 2021.12.17 |
| 확률분포 #3 - 정규분포의 정의 (0) | 2021.12.17 |
| 연속확률분포와 확률밀도함수 (0) | 2021.12.16 |



