
고등학교 확률과통계 의 마지막 내용이다.
솔직히 여기는 설명이 곤란하다.
문제에서 가정하는것부터 말이 안되기 때문에 암기시킬수밖에 없다.
- 모평균의 추정이란 무엇인가 -
한국사람의 평균 키를 조사하고 싶으면
5천만명이 넘는사람을 전부 조사할순 없으니
적당히 표본으로 몇명 뽑아서 조사한다고 했었다.
그리고 그렇게 조사된 키의 평균이
곧 표본의 평균이므로 표본평균이라 부른다고 했었다.
이번엔 드디어 이 표본평균으로
진짜 우리가 구하고자 하는 '한국사람의 평균 키'
즉 모평균을 추정해볼 것이다.
왜 구한다는 표현을 쓰지 않고
추정한다 라는 표현을 썼냐면
모평균을 정확히 구하려면 진짜 5천만명의 키를 전부 조사하는수밖에 없다.
즉 표본평균을 가지고 모평균을 추정하는 방법을 이번에 공부하는것
여기서 핵심은
단 하나의 표본평균을 가지고 모평균을 추정할것이다.
예를 들어 조사된 표본평균이 172cm 라고 해보자.
그럼 모평균이 172cm인가?
아마 그건 아닐것이다.
하지만 모평균은 대충 172cm 근처에 있겠구나. 라는건 알수 있다.
이게 이번 글의 핵심이다.
대충 표본평균 근처에 모평균이 위치할거라고 '추정'하는것이다.

- 신뢰구간과 신뢰도 -

여기서
저 '이 구간 사이 어딘가' 라는게 정확히 무슨말인가?
그니까 저건 대충 얼버무리는 말이고
정확한 수학적 표현이 어떻게되냐는거다.
여기서 말하는
'이 구간' 이 바로 '신뢰구간' 이다.

신뢰구간 사이 어딘가에 모평균이 있지 않을까? 하는건
신뢰구간 사이 어딘가에 모평균이 있을것이라고 '신뢰'하는것이기 때문에
이름이 이렇게 붙여진것이다.
근데 표본평균이 저런다고 무조건 모평균이 저 신뢰구간 사이에 있지는 않다.
이에 대한 두 가지 근거는
1. 신뢰구간의 길이를 짧게잡으면 모평균이 신뢰구간 밖으로 나가버릴수도 있음
2. 표본평균 자체가 특이케이스로 모평균과 좀 멀리 떨어져있을수도 있음
따라서 어느정도 신뢰할수 있는지를 나타내줄만한것도 필요하다.
그걸 '신뢰도' 라고 하는데,
신뢰도는 확률이다.
즉 신뢰도는 90% 이런식으로 표현된다는것이다.
만약 신뢰도가 90% 라면
신뢰구간 안에 모평균이 존재할 확률이 90%라는것이다.

신뢰구간 사이에 모평균이 존재할것이라 추정했다면
그 추정이 90%확률로 맞을거라는 말이다.
그럼 신뢰도 100%로 하면 안될까? 할수 있는데
신뢰도 100%인 자료는 의미가 없다.
신뢰도가 100%려면
신뢰구간을 엄청나게 크게 잡아야한다.
예를 들어, 한국사람의 평균 키를 조사하는데
여기서 신뢰구간을 0cm에서 1000cm로 잡으면
한국사람의 평균키는 0cm에서 1000cm 사이 어딘가에 있을테니까
신뢰도는 100%겠지만
이런 자료는 쓸모가 없다.
한국사람 평균키 조사해오랬더니
0cm에서 1000cm 사이입니다. 라고 보고하면
지금 나랑 장난하냐는 답변이 돌아올것이다.
이젠 신뢰구간의 정확한 정의를 알 시간이다.

만약 신뢰구간을
표본평균으로부터 A 만큼 떨어진 두 지점 사이의 거리로 한다면
신뢰구간은

근데 여기서 A는 그냥 내가 맘대로 잡은 값이고
정확한 표현법은 다음과 같다.


여기서 k는 신뢰상수,
σ는 모표준편차,
n은 표본의 크기 이다.
따라서 A는 표본표준편차에 신뢰상수 k를 곱한 값이다.
k값은 '신뢰도'에 따라 정해지는 값이다.
이건 암기해야한다.
그럼 '신뢰구간의 길이'는?

- 모평균의 추정 -

근데 문제가 있다.
우리가 지금 추정하고있는게 모평균이다.
모평균을 몰라서 추정하고있는데
모표준편차를 어떻게안다는말인가?
애초에 과정이 말이 안되는것이다.
그래서 문제에서는 모표준편차를 그냥 알려준다.
그리고, 이래도 맘에 안들만한 부분이
실제 상황에서는 모표준편차를 모를텐데
그럼 어떻게쓰라는건가?
실제로는 표본의 크기가 충분히 크다면
모표준편차 대신
표본표준편차를 넣어도 된다고 알려져있다.
모표준편차를 모르니 표본을 적당히 많이 뽑아서 그것의 표준편차를 구하면
모표준편차와 거의 같아질거라는 논리이다.
예를 들어, 1000명을 뽑았을때
그 1000명의 키의 표준편차나
한국사람 전체 5천만명의 표준편차나
거의 같을것이다.
알려져있다는건 증명은 여기서 다룰수 없고 그냥 외우라는것
그리고 표본표준편차는 표본평균의표준편차 와 완전히 다른것이니 오개념에 주의하자.
표본표준편차는 표본을 뽑았을 때 그 표본 하나에서의 표준편차를 말하는거다.
따라서 모평균의 추정법은 아래와 같다.
모집단이 정규분포 N(m, σ²) 을 따를때,
모평균 m은 다음 범위에 있다. 라고 추정할 수 있다.

σ = 모표준편차 또는 n이 충분히 클때 표본표준편차
n = 표본의 크기
k = 신뢰상수
- 신뢰상수의 값 -

이 식에서 하나만 알면 된다.
k값이 신뢰도에 따라 정해지는건 알겠는데
정확히 수치가 어떻게 정해지느냐를 여기서 다룰것이다.
신뢰도라는게 뭐였는지 떠올려보자.
쉽게 말해서, 저 위의 식을 만족할 확률이다.
따라서 아래와 같이 쓸수 있다.

여기서 표준화가 빠지면 섭섭하다. 표준화해보자.

따라서 신뢰도는 아래와 같이 쓸수 있다.

따라서 신뢰상수 k값의 뜻은
만약 신뢰도가 95% 라고 해보자.
그러면 P(-k≤Z≤k) = 0.95 이다.
같은논리로 신뢰도가 α%라면, P(-k≤Z≤k) = α/100 이다.
즉 신뢰상수 k값은
신뢰도가 α%가 되도록 하는 표준화된 확률변수 Z값중
최대인 값이다.
예를 들어,
신뢰도 95%의 신뢰구간은
-1.96<Z<1.96 이다.
이때 1.96이 바로
신뢰도가 95%가 되도록 하는 신뢰상수 k가 되는것이다.
- 예제 -
여기 문제는
처음보면 뭐 어쩌라는건지 어리둥절해하는 경우가 많다.
문제 유형이 다 똑같아서 몇문제 풀어보면 감을 잡는다.
1 )

석류의 무게가 정규분포를 따른다고 하니까
석류의 무게를 확률변수 X로 놓으면
확률변수 X가 정규분포 N(m, 40²) 을 따른다는 뜻이다.
그리고 지금 석류 64개를 임의추출한다음
그것의 표본평균을 이용해
농가에서 생산하는 석류의 전체적인 무게의 평균
즉 모평균을 추정하고있다.
따라서 모평균의 추정 문제이다.
따라서 c의 값은 아래와 같이 표현된다.
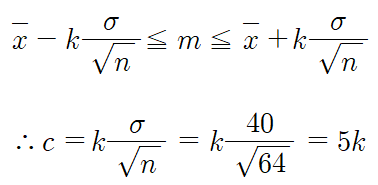
c = 5k 이다.
k값만 알아내면 된다.
아직 문제에서 쓰지 않은 조건이 있다.

0.495의 의미가 무엇일까?
P(0≤Z≤2.58) = 0.495 이므로
P(-2.58≤Z≤2.58) = 0.495 × 2 = 0.99 이다.
따라서 신뢰도 99%의 신뢰구간이 -2.58≤Z≤2.58 이다.
따라서 k = 2.58 이다.
이 개념을 처음 공부하는거라면
P(0≤Z≤2.58) = 0.495 이므로
P(-2.58≤Z≤2.58) = 0.99 라는걸 생각해내는 과정이 안될수 있는데
그게 내가 아까 말했던 처음 접할때의 어리둥절함이고
몇문제 풀어보면 바로 감을 잡는다.
아무튼 c = 5k 인데 k = 2.58이므로
c = 12.9 이다.
따라서 답은 4번
2 )

고객의 주문 대기 시간을 확률변수 X라 하면
확률변수 X는 정규분포 N(m, σ²) 을 따른다.
근데 여기서 64명을 임의추출한다음 표본평균을 이용해서
전체 고객의 주문대기시간의 평균 m을 추정한다고 한다.
이것도 표본평균을 이용해 모평균을 추정하는 문제이다.
신뢰구간이 a≤m≤b 인데
b-a=4.9 라고 한다.
여기서 b-a의 의미는
신뢰구간에서의 최댓값 - 최솟값 이니까
'신뢰구간의 길이' 이다.

여기서 n=64 이고,
여기서 k의 값은
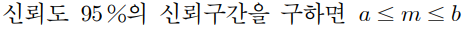
이 문장과
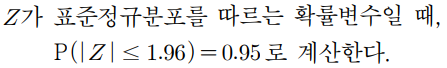
이 문장에 따라서
k = 1.96 임을 추론할수 있다.
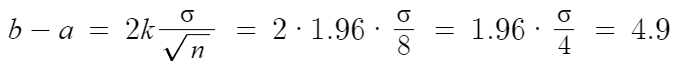
따라서 이 식을 정리하면
σ = 10 임을 구할 수 있다.
따라서 답은 10
확통 끝
'확률과 통계 > III. 통계' 카테고리의 다른 글
| 통계적 추정 #2 - 표본평균의 분포와 표준화 (0) | 2021.12.20 |
|---|---|
| 통계적 추정 #1 - 표본평균의 평균, 분산, 표준편차 (0) | 2021.12.20 |
| 확률분포 #5 - 정규분포와 이항분포의 관계 (0) | 2021.12.17 |
| 확률분포 #4 - 정규분포의 표준화 (0) | 2021.12.17 |
| 확률분포 #3 - 정규분포의 정의 (0) | 2021.12.17 |



