
혹시 본인이 못 푼 문제인데
어떻게 푸는건지 궁금해서 이 글을 보는거라면
이 글을 보지 말것.
남이 풀어주는걸로는 실력이 늘지 않는다.
풀긴 풀었는데 풀면서 100%확신하진 못하고 약간 찜찜했거나
다른 풀이도 있을까 해서 찾아보는거라면
매우 환영이다.
원하시는 문제로 바로 가고싶으면
N번 문제로 가고싶다면
N )
이 형태로 검색하시면 됩니다.
예를들어 24번으로 가고싶으면 24 )
쉬운건 빠르게 넘어가면서
비약 하나도 없이 풀어보겠습니다.
23 )

이항정리의 기본 예제이다.
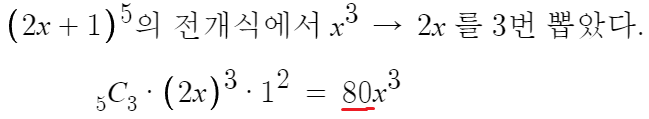
따라서 답은 4번
24 )


일단 이부분에서 조건부확률 문제임을 파악하는게 중요하다.
이것만 파악하면 바로 풀리는 문제이다.
- 첫번째 풀이 : 공식풀이 -
임의로 선택한 한명이 1학년인 사건을 X라 하면
임의로 선택한 한명이 1학년일 확률은 P(X)이며
임의로 선택한 한명이 진로활동 B를 선택할 확률을 P(B)라 하면
임의로 선택한 한명이 진로활동 B를 선택한 학생일때,
이 학생이 1학년이기까지 할 확률은
조건부확률의 정의인, B일 때 X일 확률 : P(X|B) 이다.
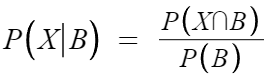
P(X∩B) = 5/20, P(B) = 9/20
따라서 P(X|B) = 5/9
따라서 답은 2번
- 두번째 풀이 : 논리로만 풀이 -
B를 선택한 학생 수 : 9
B를 선택한 학생중 1학년인 학생 수 : 5
따라서 5/9이고 답은 2번
25 )

'서로다른' 숫자 5개중에서
'중복을 허락'하여 4개를 택해서 '일렬로 나열'한다고 한다.
따라서 이건 중복순열 문제이다.
확률을 p라고 하면
p = (3500보다 큰 경우의 수) / (전체 경우의 수)
전체 경우의 수는 5개중 중복허락 4개택해서 일렬로나열하는거니까
전체 경우의 수 = 5⁴ 이다.

우선 3500보다 크려면
3 이상의 수로 시작해야한다.
즉 3xxx 또는 4xxx 또는 5xxx 형태이다.
근데 4xxx거나 5xxx면
뒤에 어떤 숫자가 오든 무조건 3500보다 크기때문에
맨 앞자리 숫자가 4 이상이면 무조건 3500보다 크다는 결론에 도달한다.
따라서 3500보다 큰 경우의 수 =
(3으로 시작하는것중 3500 이상인 경우의 수) + (4이상의 수로 시작하는 경우의 수)
4 이상의 수로 시작하는 경우의 수는
일단 4랑 5중 하나를 맨 앞에 세운다. 이때 경우의수 2
그다음 나머지 3개는 숫자 5개중 아무거나 뽑아서 나열한다.
이때 경우의수 5³
따라서 4 이상의 수로 시작하는 경우의 수는
2×5³
그리고 3으로 시작하는것중 3500 이상이려면
우선 앞에서 두번째 숫자가 5여야한다.
즉 35xx 형태여야한다.
근데 35로 시작하면 뒷자리 두개가 뭐가 오든 무조건 3500보다 크다.
따라서 3으로 시작하는것중 3500 이상인 경우의 수 =
35로 시작하는 경우의 수
따라서 35 뒤의 두자리만 나열하면 되고
그런 경우의 수는 5²
따라서 종합하자면
3으로 시작하는것중 3500 이상인 경우의 수 = 5²
4이상의 수로 시작하는 경우의 수 = 2×5³
따라서 p는
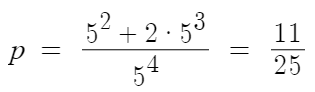
따라서 답은 3번
26 )

이 문제를 틀렸거나 적당히 찍어맞췄다면 이 부분의 개념을 주의깊게 점검해야한다.
숫자만 조금 바꾸면 난이도가 확 오를 문제이며, 그렇게 출제할 가능성도 충분하다.
아무튼 풀이시작
3가지 색의 카드를 각각 한장 이상 받는 학생이 있도록 나누어주라고 한다.
쉽게 말해서 3가지 색의 카드를 다 가지는 학생이 존재하도록 하라는거다.
근데 아주 자비롭게도 노란색카드가 1장밖에 없다.
따라서 3가지 색의 카드를 다 가지는 학생은 1명 존재할것이다.
그럼 일단 이 1명에게 빨강파랑노랑 카드 한장씩 주자.
3명중 1명 골라줄거니까 이때 경우의수는 3
빨간색 3장, 파란색 1장 남았다.
카드를 받지 못하는 학생이 있을수 있으니
꼭 나머지 2명에게 나눠줘야한다는 법은 없다.
한명이 7장을 다 가질수도 있다.
그리고 같은색 카드끼리는 서로 구별하지 않는다고 하니
빨간카드를 '몇장' 갖느냐, 파란카드를 '몇장' 갖느냐가 학생의 관심사이다.
따라서 몇장씩 나눠줄것인지만 구하면 된다.
빨간색 3장, 파란색 1장을
3명에게 나눠줄것이다.
여기서 문제는
나눠주는 사람끼리는 구별이 가능하기 때문에
파란색카드 1장을 나눠주는 경우의 수는 3이다.
그리고 빨간색 카드를 나눠주는 경우의 수는
각각의 학생이 받는 카드의 수를 x, y, z 라 하면
x+y+z=3 이다.
그리고 x,y,z는 음이 아닌 정수이다.
따라서 빨간카드 3개를 3명에게 나눠주는 경우의 수는
₃H₃ = 10 이다.
처음에 카드 색깔별로 한장씩 줄 사람 정하는 경우의수 3
파란카드 1장 남은거 줄사람 정하는 경우의수 3
빨간카드 3장 남은거 줄사람 정하는 경우의수 10
따라서 경우의수는 3×3×10 = 90
따라서 답은 3번
27 )

각각의 주사위는 독립시행이며
각각의 동전도 독립시행이며
주사위와 동전도 독립시행이다.
따라서 독립시행의 확률 문제이다.
일단 확률문제니까 전체 경우의수부터 구하자.
주사위 하나당 경우의수 6이고
동전 하나당 경우의수 2니까
전체 경우의수는 6²×2⁴ 이다.
이제 조건을 만족하는 경우의수를 구할건데
우선 주사위의 눈의 수의 곱과
앞면이 나오는 동전의 개수가 같으려면 어떻게 되어야하는지부터 보자.
앞면이 나오는 동전의 개수는
0, 1, 2, 3, 4 중 하나이다.
그리고 주사위의 눈의 수의 곱이
저것중 하나에 해당되어야 한다.
우선 0은 탈락이다.
주사위의 눈은 1~6중 하나이기 때문이다.
그럼 1, 2, 3, 4중 하나일거다.
- 1인 경우의 수 -
우선 앞면나오는 동전이 1개여야한다.
동전 4개중 1개가 앞면이다.
그런 경우의 수는 동전이 4개니까 4이다.
주사위의 눈의 수의 곱이 1이 되려면
주사위가 둘다 1이 나와야한다.
따라서 이때 경우의 수는 1
따라서 1인 경우의 수는 4×1 = 4
- 2인 경우의 수 -
우선 앞면나오는 동전이 2개여야한다.
동전 4개중 2개가 앞면이다.
그런 경우의 수는
동전 4개중 2개 앞면나올거 뽑으면 된다.
₄C₂ = 6
주사위의 눈의 수의 곱이 2가 되려면
주사위가 하나는 1, 하나는 2가 나와야한다.
따라서 이때 경우의 수는 2
따라서 2인 경우의 수는 6×2 = 12
- 3인 경우의 수 -
우선 앞면나오는 동전이 3개여야한다.
동전 4개중 3개가 앞면이다.
그런 경우의 수는
동전 4개중 3개 앞면나올거 뽑으면 된다.
₄C₃ = 4
주사위의 눈의 수의 곱이 3이 되려면
주사위가 하나는 1, 하나는 3이 나와야한다.
따라서 이때 경우의 수는 2
따라서 3인 경우의 수는 4×2 = 8
- 4인 경우의 수 -
우선 앞면나오는 동전이 4개여야한다.
4개 다 앞면나와야하므로 그런 경우의 수는 1
주사위의 눈의 수의 곱이 4가 되려면
주사위가 (1,4), (4,1), (2,2) 중 하나가 나와야한다.
따라서 이때 경우의 수는 3
따라서 4인 경우의 수는 1×3 = 3
따라서 전부 더하면 4+12+8+3 = 27
따라서 확률은
27 / (6²×2⁴) = 3/64
따라서 답은 1번
28 )

주사위를 4번 던져서 얻은 점수의 합이 4가 되도록 할때
던지는 과정에서 나왔을 주사위의 눈의 수의 경우의 수가 몇개냐는거다.
여기서는 나온 눈의 수를 차례로 a, b, c, d라 한다음
순서쌍 (a, b, c, d)의 개수를 구하라 했으니까
예를들어, 주사위에서 2의 눈이 1번 나왔다면
주사위에서 2의 눈이 1번 나왔다는것을 넘어서
2의 눈이 1번 언제 나왔는지까지 생각해야한다.
여기서는 아주 자비롭게도
나온 눈의 수가 4 이상이면 0점을 얻으라고 한다.
즉 4 이상이 나오면 꽝
따라서 꽝이 몇번나왔는지를 기준으로 볼것이다.
- 꽝이 4번 -
꽝이 4번이면 점수의 총합이 0이므로
조건을 만족하지 못한다.
- 꽝이 3번 -
꽝이 3번이면
점수의 총합이 4가 되기 위해
꽝이 아닌 그 한번의 기회에서 4점을 얻어야하는데
4 이상의 눈이 나오면 꽝으로 처리한다 했으므로
한번에 4점을 얻을 방법이 없다.
따라서 조건을 만족하지 못한다.
- 꽝이 2번 -
꽝이 2번이면
점수의 총합이 4가 되기 위해
꽝이 아닌 두번의 기회에서 4점을 얻어야한다.
가능한 점수 조합은
1점3점, 2점2점 이다.
1점3점인 경우는
1의 눈이 한번
3의 눈이 한번
4 이상의 눈이 두번
나왔다는거다.
1점을 얻는 경우는
4번의 기회니까 4가지이다.
그다음 3점을 얻는 경우는
4번의 기회중 아까 1점얻을때 기회 한번 썼으니
3번의 기회중 하나에 들어갈거고 3가지이다.
나머지 2번의 기회에선 둘다 4 이상의 눈이 나와서 꽝이었다.
꽝이기만 하면 되기때문에 4이상 이기만 하면 된다.
4 이상의 눈이 나오는 경우의 수는 4,5,6 으로 3이다.
따라서 꽝두개 나오는 경우의수는 3×3 = 9
따라서 1점3점인 경우의수는
4×3×9 = 108
그다음 2점2점인 경우는
2의 눈이 두번
4 이상의 눈이 두번
나왔다는거다.
2의 눈이 두번 나오는 경우의 수는
네번의 기회중 두자리 들어가면 되니까
₄C₂ = 6
그리고 4 이상의 눈이 두번 나올 경우의 수는
3×3 = 9
따라서 2점2점인 경우의수는 6×9 = 54
따라서 꽝이 2번 나오는 경우의 수는
108+54 = 162
- 꽝이 1번 -
꽝이 1번이면
점수의 총합이 4가 되기 위해
꽝이 아닌 3번의 기회에서 4점을 얻어야한다.
가능한 조합은 1점1점2점 뿐이다.
우선 2점을 얻는 경우는
네번의 기회중 1번이었을테니 경우의수는 4
그다음 1점 두번 얻는 경우는
나머지 세번의 기회중 2번이었을테니
경우의수는 ₃C₂ = 3
그다음 꽝은 한번 나오니까
경우의수는 3
따라서 꽝이 1번 나오는 경우의 수는
4×3×3 = 36
- 꽝이 0번 -
꽝이 0번이면
가능한 조합은 1점1점1점1점 이다.
따라서 가능한 경우는 네번다 1의 눈이 나오는 경우 뿐이다.
따라서 꽝이 0번 나오는 경우의 수는 1
따라서 전부 더하면
162+36+1 = 199
따라서 답은 5번
29 )

개인적으로 이 시험지에서 가장 어려웠던 확통문제
경우를 좀 많이 나눠야해서 귀찮고
단답형이라 실수할 확률도 높은 문제이다.
솔직히 그림은 왜 넣어준건지 모르겠다.
전혀 도움이 안되고 오히려 헷갈리게만든다.
그림 무시하고 풀면 된다.
그리고 이게 글로 설명하는데 한계가 있어서
쓰고보니 좀 난잡한게 있다.
맨 아래에 한장풀이 있으니
글이 난잡해서 보기 힘들면 그것도 보자.
우선 1, 2, 3, 4, 5, 6을
자리 6개 있는 원탁에 앉힐건데
서로 이웃한 두자리에 적혀있는 수의 곱이 12가 되면 안된다고한다.
1, 2, 3, 4, 5, 6 중 두개 골라서 12를 만들수 있는 조합은
2×6 = 12
3×4 = 12
이거 두개뿐이다.
즉 2와 6은 같이 앉히면 안되고
3과 4도 같이 앉히면 안된다.
1과 5는 뭐랑 곱해도 12가 안되기 때문에
그냥 아무렇게나 앉혀도 된다.
따라서 일단 처리 곤란한 2, 3, 4, 6을 먼저 처리할것이다.
1과 5는 그냥 남는자리 보내면 되는것이다.
일단 난 2를 먼저 앉히겠다.
원탁이고 문제에서 회전하여 일치하는것은 같은것으로 보라했으므로
2가 처음 앉는 경우의 수는 1이다.
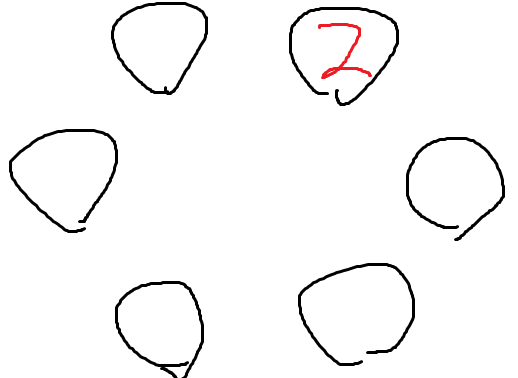
그냥 아무데나 앉혔다.
2×6 = 12 니까
6은 2와 같이 생각할것이다.
2를 앉혔으니까 이제 6을 앉힐거라는거다.
6이 앉을수 있는곳은 세군데이다.
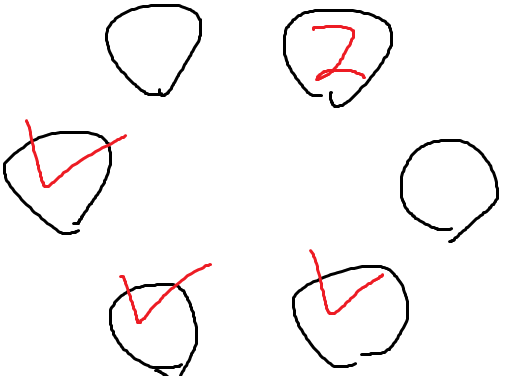
근데 바로 경우의수 3 이런식으로 처리하진 않을거다.
왜냐면
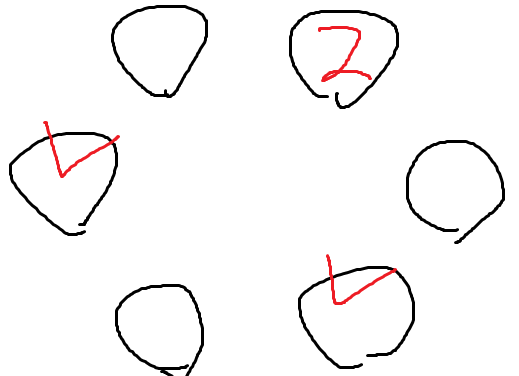
이 두자리는 2와 두칸 떨어진 자리이고
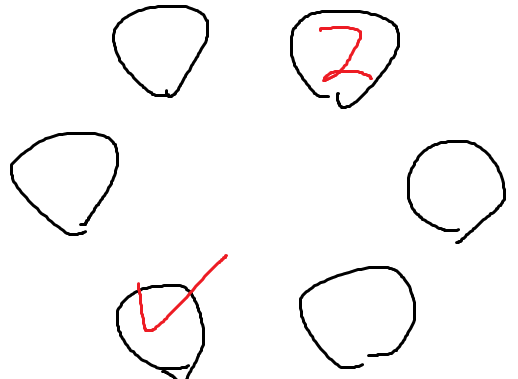
이 자리는 2와 완전히 반대편인 자리이기 때문에
이 두 경우에서 조금 다른 양상이 펼쳐진다.
그 이유는 풀면서 설명해주겠다.
우선 2와 두칸떨어진 자리에 6을 앉힌 경우부터 해보자.

6을 앉히는 경우의 수는 2
일단 앉힌다음 더 분석해보자.
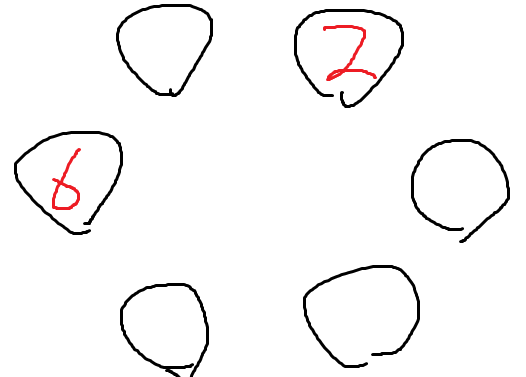
2와 6을 처리완료했다.
이제 또 처리곤란한게 3과 4이다.
이번엔 3과 4를 앉힐것이다.
3을 아무데나 앉힐거긴 한데
좀 특이해보이는 자리가 있다.
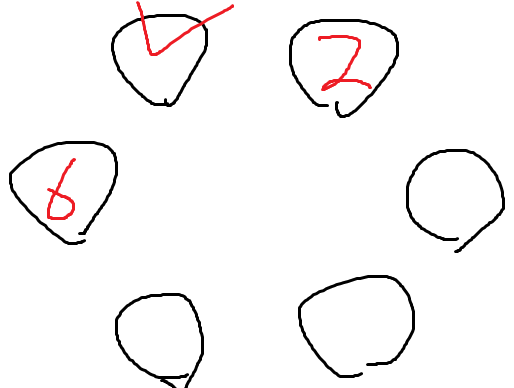
2와 6 사이인 이 자리 이다.
왜 특이하냐면
3 입장에서 여기 앉으면
무조건 4와 떨어져 앉기 때문에 조건을 만족하며
4입장에서의 경우도 마찬가지다.
따라서 이것도 경우를 나눠서 생각해야한다.
특이한 자리에 앉는 경우와
특이하지 않은 자리에 앉는 경우
- 특이한 자리에 앉는 경우 -
우선 이 특이한 자리에 3과 4중 하나를 앉힌다.
이때 경우의수 2
그리고 3과 4중 나머지 하나는 아무데나 앉아도 서로 떨어지기때문에
아무데나 앉혀도 된다.
따라서 이때 남는거 앉히는 경우의수 3
따라서 3과 4를 특이한 자리에 앉히는 경우의 수는
2×3 = 6
- 특이하지 않은 자리에 앉는 경우 -
이 경우는 3과 4가 갈수있는 자리가 정해져있다.
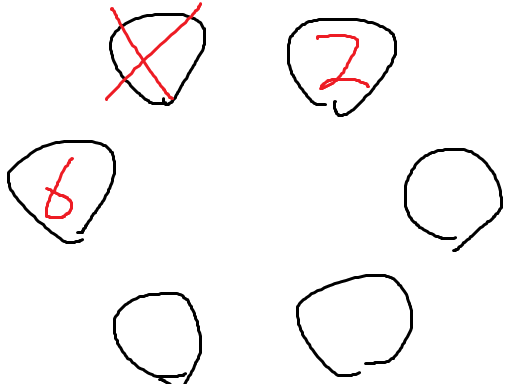
우선 특이하지 않은 자리에 앉는경우를 분석하는거니까
특이한 자리에 앉히는 것 자체는 아예 생각하지 말아야한다.
여기서 3을 가운데자리에 앉혀보자.
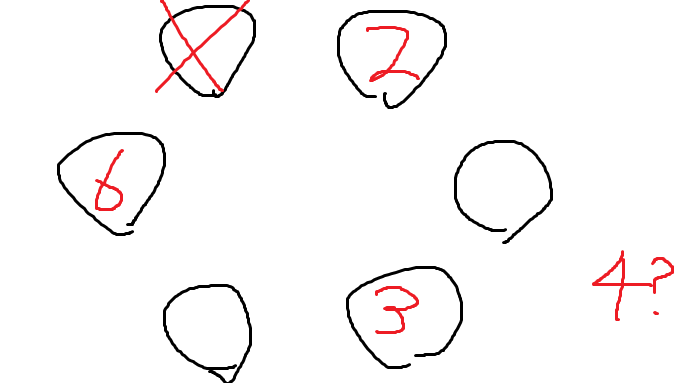
4가 갈곳을 잃었다.
어디 앉아도 3과 이웃하게되기 때문이다.
따라서 3과 4가 갈수있는 자리는
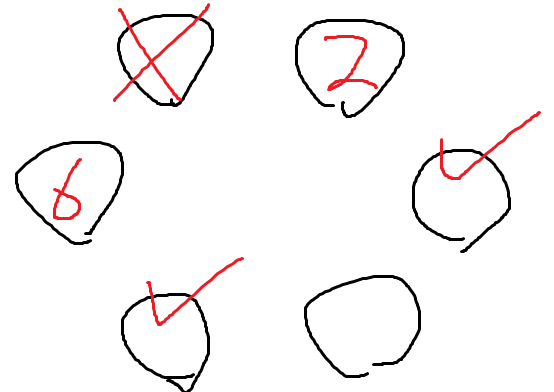
이 두자리 뿐이며
이 두자리에 3과 4를 앉히는 경우의 수는 2×1 = 2
따라서 특이하지 않은 자리에 앉히는 경우의 수는 2
따라서 3과 4를 앉히는 경우의 수는
6+2 = 8
지금까지 뭘했냐면
2, 6, 3, 4 를 앉혔다.
단, 6은 2와 두칸 떨어진 자리에 앉는다.
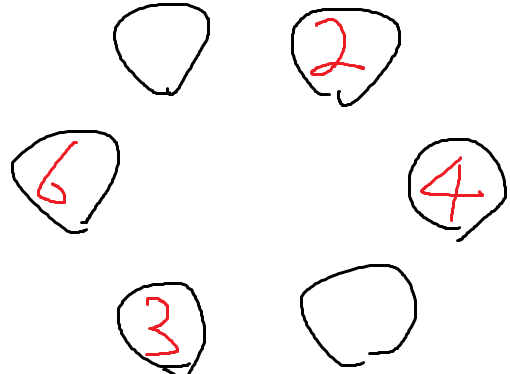
여기까지 경우의 수는
(6앉히는경우의수) 2 × (3과4앉히는경우의수) 8 = 16
이제 6과 2가 완전 반대편 자리에 앉는 경우를 할 차례이다.
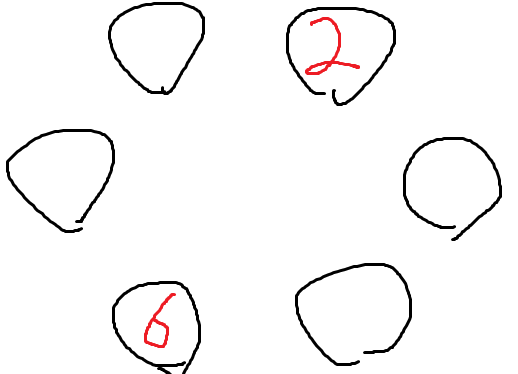
6이 2 완전 반대편 자리에 앉는 경우의 수는 1
이제 3과 4를 앉힐건데
이건 아까보다 간단한게
딱히 특이한자리라고 할게 없다.
식 한줄로 처리할수 있다.
3을 아무데나 앉힌다음
4를 3과 떨어지게만 앉히면 된다.
3을 앉히는 경우의 수는 4
4를 앉히는 경우의 수는
3과 떨어져야하므로 2
따라서 3과 4를 앉히는 경우의 수는 4×2 = 8
따라서 6과 2가 완전 반대편 자리에 앉는 경우의 수는
1×8 = 8
따라서 2, 6, 3, 4 를 앉히는 경우의 수는
(2와 6이 두칸떨어지게 앉는 경우의 수) + (2와 6이 완전 반대편자리에 앉는 경우의 수)
혹시 왜 이걸 덧셈연산하는지 모른다면 가볍게 설명해주겠다.
이 두개는 한번의 시행에서 동시에 일어날수 없는일이다.
즉 숫자들을 앉힌다는 '시행'에서
2와 6이 두칸떨어지게 앉는거랑
2와 6이 완전 반대편자리에 앉는거는 동시에 일어날수가 없으니까
이건 덧셈연산해야한다.
2와 6이 두칸떨어지게 앉는 경우의 수 = 16
2와 6이 완전 반대편자리에 앉는 경우의 수 = 8
따라서 2, 6, 3, 4 를 앉히는 경우의 수는 24
이제 진짜 2, 6, 3, 4를 전부 앉혔다.
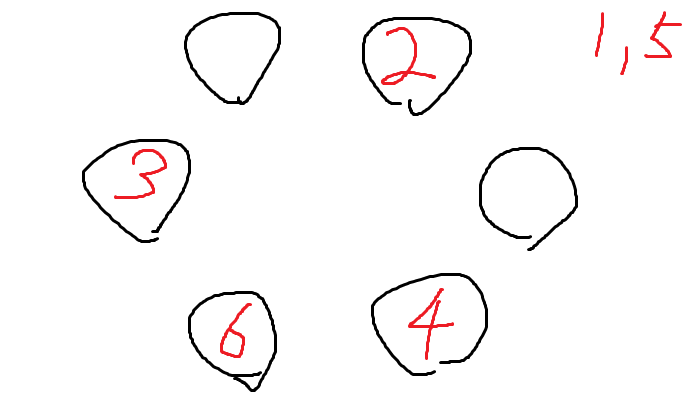
1과 5만 앉히면 되는데
얘네는 아무 제약없으니까 아무데나 앉혀도 된다.
따라서 이때 경우의 수는 2
따라서 답은
24×2 = 48
- 한장풀이 -
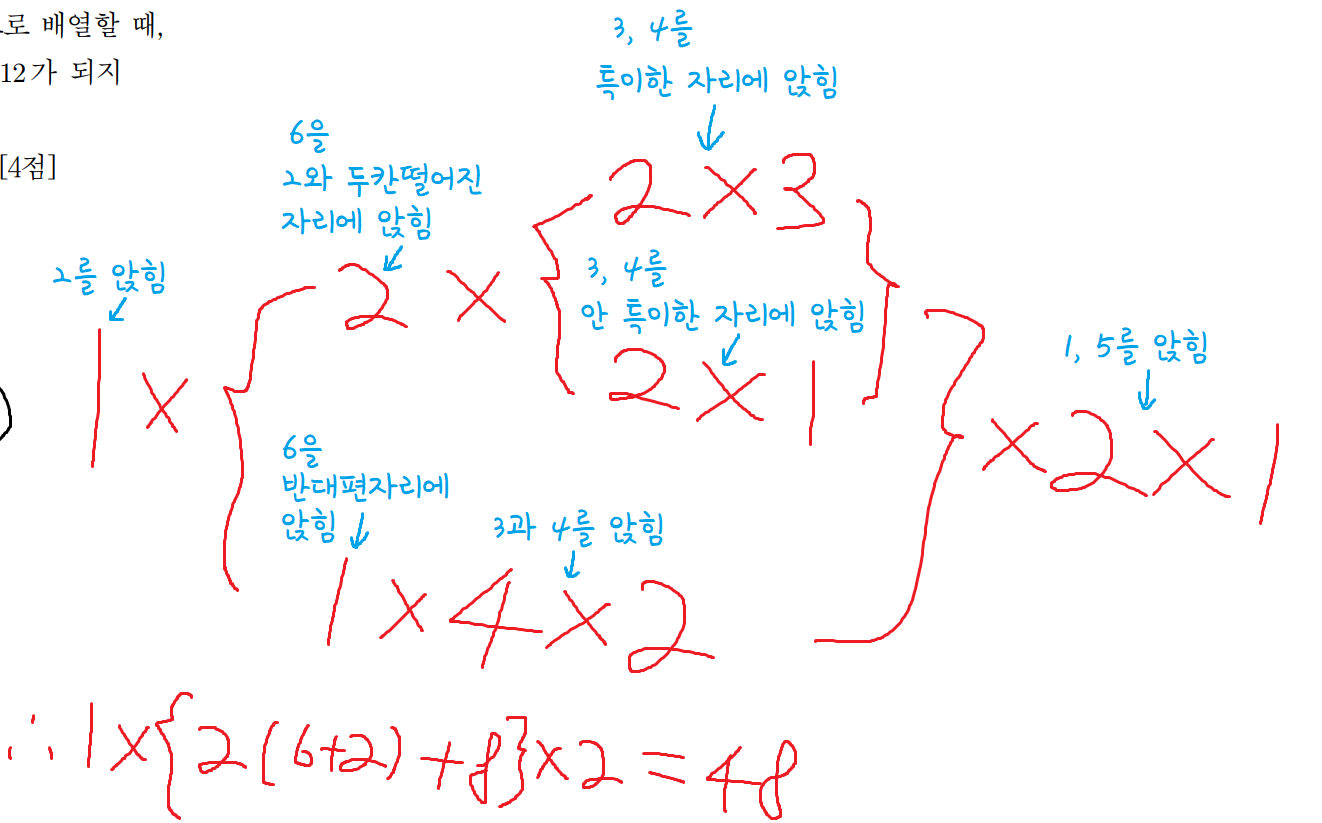
30 )

개인적으로 29번보다 쉬웠던 문제
우선 확률문제니 전체 경우의 수부터 구해보자.
3개중 하나 꺼내는 시행을 5회 반복하며
꺼냈던걸 다시 넣은다음 임의로 꺼내는것이므로
각 시행은 독립시행이다.
따라서 전체 경우의 수는
3^5 = 243
이제 조건을 만족하는 경우의 수를 구해보자.
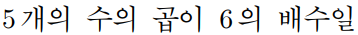
5개 수의 곱이 6의 배수이다 라는 말은
5개의 수를 곱한것중에서
2×3 이 존재한다는 말이다.
즉 5개의 수 중 2와 3은 최소 하나씩은 존재해야한다.
여기서 핵심은
2와 3이 최소 하나씩 존재하는 경우의 수를 구하는거면
전체 경우에서
2 또는 3이 하나도 존재하지 않는 경우의 수를 빼주는게 더 쉬울거다.
즉 여사건을 이용하여 풀것이다.
2 또는 3이 하나도 존재하지 않는 경우의 수는
(2가 하나도 존재하지 않는 경우) + (3이 하나도 존재하지 않는 경우)
그리고 여기서 2와 3이 둘다 존재하지 않을수도 있으므로
저 식은 2와 3이 둘다 존재하지 않는경우를 두번 더한거고
따라서 한번 빼줘야한다.
(2가 하나도 존재하지 않는 경우) + (3이 하나도 존재하지 않는 경우)
- (2와 3이 둘다 존재하지 않는경우)
- 2가 하나도 존재하지 않는 경우 -
5개의 수는 1과 3으로만 구성되었다.
1과 3중 하나 뽑아서 5자리 배열할건데
뽑힌숫자가 또뽑힐수도 있으니 중복허용이다.
따라서 중복순열이고
이것의 경우의 수는 2^5 = 32 이다.
- 3이 하나도 존재하지 않는 경우 -
5개의 수는 1과 2로만 구성되었고
같은 논리로
이것의 경우의 수는 2^5 = 32 이다.
- 2와 3이 둘다 존재하지 않는 경우 -
5개의 수는 1로만 구성되었다.
그런 경우는 한가지밖에 없다.
따라서 이것의 경우의 수는 1이다.
따라서 2 또는 3이 하나도 존재하지 않는 경우의 수는
32 + 32 - 1 = 63
전체 경우의 수가 3^5 = 243 이므로
구하고자 하는 확률은
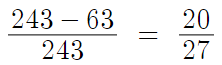
따라서 p=27, q=20
따라서 답은 27+20 = 47
'2022학년도 기출 해설 > 2022학년도 6월 모의평가 해설' 카테고리의 다른 글
| 2022학년도 6월 모의평가 물리II 해설 (0) | 2021.09.01 |
|---|---|
| 2022학년도 6월 모의평가 물리I 해설 (0) | 2021.08.31 |
| 2022학년도 6월 모의평가 수학 미적분 23번~30번 해설 (0) | 2021.08.31 |
| 2022학년도 6월 모의평가 수학 공통 16번~22번 해설 (0) | 2021.08.30 |
| 2022학년도 6월 모의평가 수학 공통 1번~15번 해설 (0) | 2021.08.30 |



