
혹시 본인이 못 푼 문제인데
어떻게 푸는건지 궁금해서 이 글을 보는거라면
이 글을 보지 말것.
남이 풀어주는걸로는 실력이 늘지 않는다.
풀긴 풀었는데 풀면서 100%확신하진 못하고 약간 찜찜했거나
다른 풀이도 있을까 해서 찾아보는거라면
매우 환영이다.
원하시는 문제로 바로 가고싶으면
N번 문제로 가고싶다면
N )
이 형태로 검색하시면 됩니다.
예를들어 2번으로 가고싶으면 2 )
쉬운건 빠르게 넘어가면서
비약 하나도 없이 풀어보겠습니다.
1 )

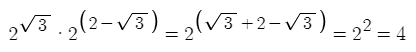
따라서 답은 4번
2 )

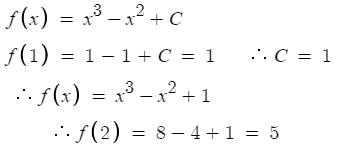
따라서 답은 5번
3 )


따라서 답은 1번
4 )
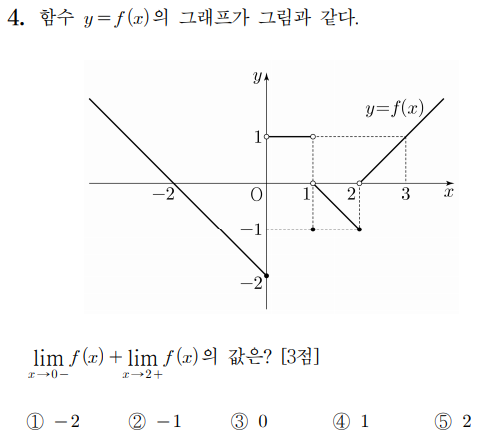
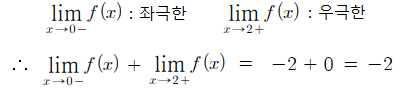
따라서 답은 1번
5 )

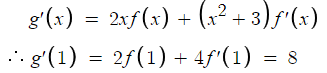
따라서 답은 3번
6 )

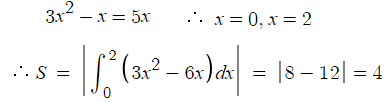
따라서 답은 4번
7 )

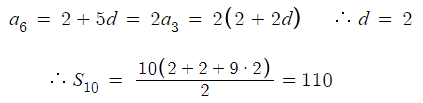
따라서 답은 2번
8 )


따라서 답은 4번
9 )

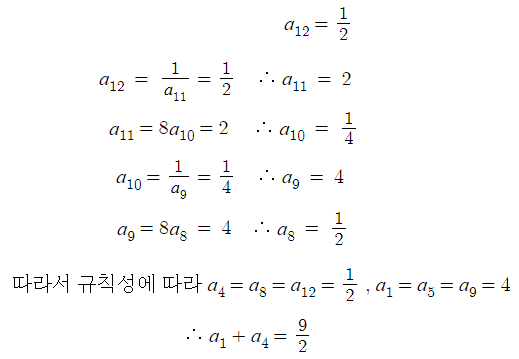
따라서 답은 5번
10 )


따라서 답은 2번
11 )

1. 함수 f(x)는 닫힌구간 [0,1]에서 연속이고
그 구간에서의 적분값이 주어져있다.
2. f(0)=0 , f(1)=1 이다.
이 조건을 만족하는 함수를 아무렇게나 그리면 된다.
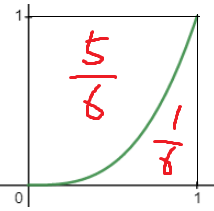
함수가 꼬불꼬불하게 생길수도 있지만
문제에서 준 조건만 만족하면 되므로
그냥 본인이 편한대로 그리면 된다.
난 이게 편하니까 이렇게 그렸다.
가로 1 세로 1인 사각형의 넓이는 1이고
거기까지의 적분값이 1/6 이니까
나머지부분은 5/6 임을 알 수 있다.
이제 (가) 조건을 뜯어보자.
g(x)는
0≤x≤1 이면 f(x)이고
-1<x<0 이면 f(x)를 x방향으로 -1만큼 평행이동하고
y축대칭으로 뒤집은다음 1을 더한것이다.
즉 g(x)는 -1<x≤1 에서 이렇게 그려질것이다.
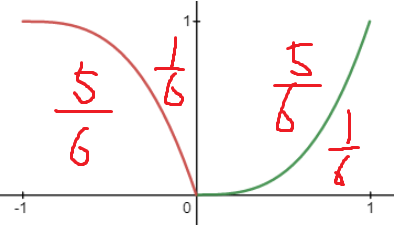
그리고 (나) 조건에 의해
g(x)는 주기가 2이고
g(-1)=g(1) 이므로 g(x)는 이렇게 그려질것이다.

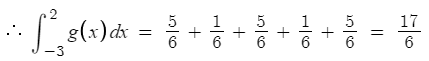
따라서 답은 2번
12 )
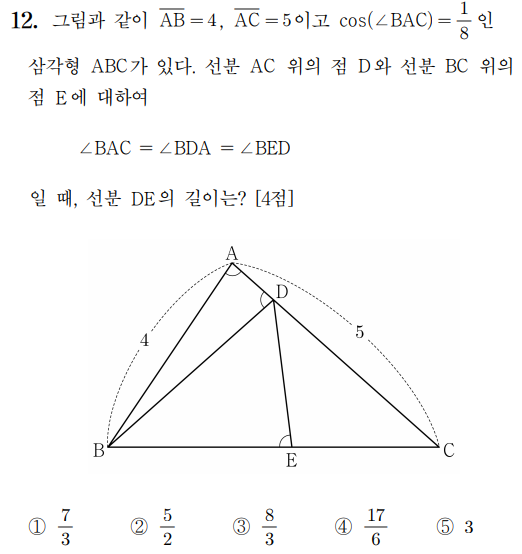
1. ∠BAC = ∠BDA 임을 이용해 BD=4 임을 알아낸다.
2. cos(∠BAC) = 1/8 인것과
이등변삼각형의 밑변에 중점에 선분을 내리면
직각이등분선이 된다는걸 이용하여
AD의 길이를 구하고
CD=4 와 함께 삼각형 BCD는 이등변삼각형임을 알아낸다.
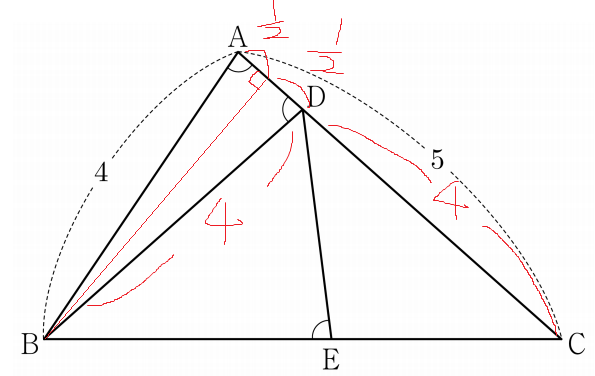
이게 2번과정까지 한것이다.
3. 코사인법칙을 이용해 BC의 길이를 알아낸다.
BC의 길이를 x라 한다.

4. ∠BAC = θ 라 하면 ∠BCD와 ∠BCD 를 θ로 표현할 수 있다.
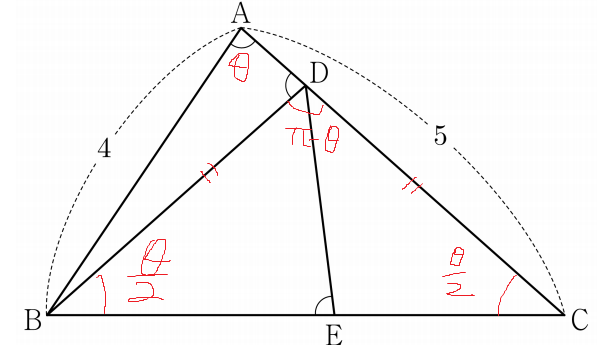
5. 삼각형 BDE에 사인법칙을 적용하면 최종적인 답이 나온다.
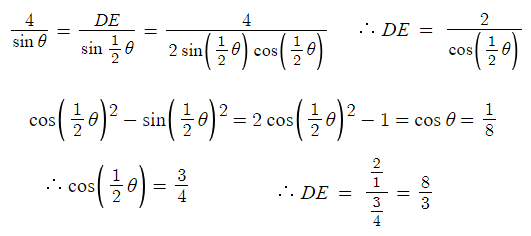
따라서 답은 3번
13 )

일단 f(x)는 주기가 1이고
f(x) 함수를 그리면

이런 식으로 그려질것이다.
저 파란 점은 구멍뚫린부분이다.
따라서 f( sqrt(k) ) 의 값은
sqrt(k) 가 정수일때 1이고
나머지는 3이다.
k=1부터 20까지 더한다 했으니
그 범위 안에서 sqrt(k)가 정수가 되도록 하는 k는
1, 4, 9, 16이다.
따라서
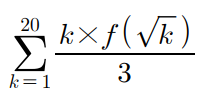
이 값은
k = 1, 4, 9, 16일때는 k/3이고
나머지일때는 k이다.
근데 1, 4, 9, 16만 빼놓고 1부터 20까지 k의 값을 모두 더하는건
시간도 오래걸리고 체력도 많이 빠지기때문에
그냥 1부터 20까지 f( sqrt(k) ) = 3 이라 하고
k=1부터 k=20까지 다 더해버린다음
f( sqrt(k) ) = 1 인 부분은 더하면 안되니까 빼고
다시 f( sqrt(k) ) = 1 인 부분을 각각 k/3 으로 더해줄것이다.
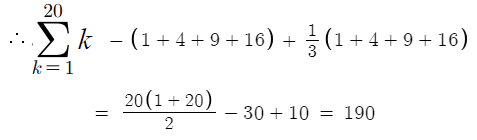
따라서 답은 5번
14 )


근데 g(x)는 연속함수이고
f(x-p)+q 는 삼차함수 f(x)를 평행이동한것 뿐이다.
따라서 x가 0이 아닌 부분은 일단 무조건 연속이다.
따라서 x=0일때만 연속이면 되고
이를 만족하는 g(0)값을 구해보면
g(0) = | f(-p)+q | = -| f(-p)+q |
따라서 g(0) = 0
이제 f(x)의 그래프를 그려보자.
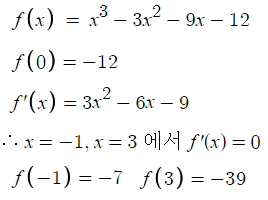
f'(x)=0을 만족하는 x가 두갠데
삼차함수이므로 각각 극대점 극소점일거고
최고차항의 계수가 양수이므로
극대점과 극소점을 표시한다음
x가 작아지면 내려가고
커지면 올라가는 그래프를 적당히 그리면 된다.
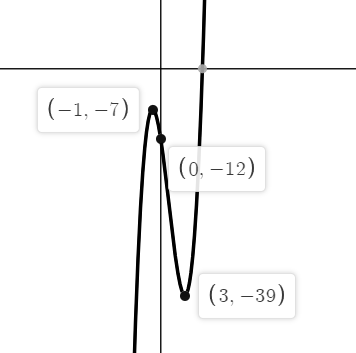
g(x)는 여기서 x 방향으로 p 만큼
y 방향으로 q 만큼 평행이동한 뒤
x가 양수면 전부 절댓값취해서 x축 위로 올려버리고
x가 음수면 전부 절댓값취해서 x축 위로 올려버린다음
다시 -1 곱해서 x축 아래로 내려버린 그래프이다.
p, q는 문제에서 양수라고 줬으므로
여기서 f(x)는 무조건 오른쪽 위 방향으로 평행이동된다.
g(x) 그래프 그리는 방법
x가 양수일때는
함숫값이 음수인부분을
전부 x축 위로 올려버리고
x가 음수일때는
힘숫값이 음수인 부분을
전부 x축을 위로 올려버린다음
절댓값에 음수를 붙이는거니까 x<0인 부분의 그래프 전체를
다시 뒤집으면 된다.
따라서 x가 음수일때
함숫값도 전부 음수라면
(함숫값이 음수라서 절댓값취할때 뒤집어줘야하는 부분)
=
(마지막에 음수 붙이니까 뒤집어줘야하는 전체 부분) 이므로
똑같은걸 두번 뒤집으면 그대로니까
그대로 놔두면 그게 g(x)의 x<0 부분 그래프다.
즉 x<0에서 f(x)를 평행이동한 그래프의 함숫값이 음수이면
x=0에서 미분 가능한 함수가 나온다.
절댓값 취한것때문에 꺾이지 않고 그대로 가기 때문이다.
일단 이건 여러가지 경우로 나눠서 생각해볼건데
어떤 방향으로 갈거냐면
평행이동시킨 그래프가 있으면
x축은 어느 지점을 지날것인지 로 나눌것이다.
그러면 5가지가 나온다.
1. x축이 극댓값보다 위에 있는 경우
2. x축이 딱 극댓값에 있는 경우
3. x축이 극댓값과 극솟값의 사이에 있는 경우
4. x축이 딱 극솟값에 있는 경우
5. x축이 극솟값보다 아래에 있는 경우
1. x축이 극댓값보다 위에 있는 경우
이런 경우는 없다.
왜냐면 g(x)=0이어야 하기 때문이다.
이런 경우가 가능하려면 그래프를 왼쪽으로 평행이동 해야하는데
p가 양수이므로 그래프를 왼쪽으로 평행이동하는건 생각하지 않는다.
2. x축이 딱 극댓값에 있는 경우
여기서 g(x)를 그려보자.
그러면 이런 그래프가 나온다.
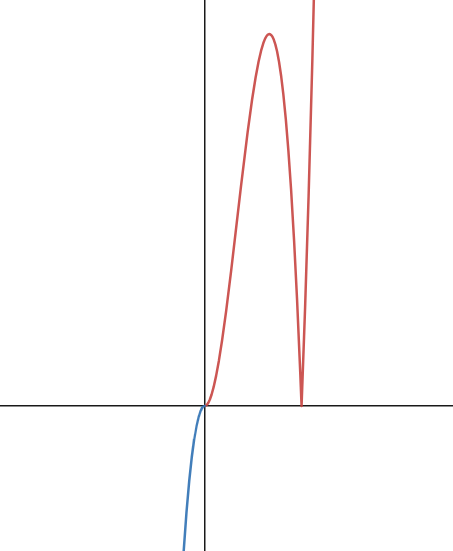
일단 x>0 인곳에서 미분불가능점이 하나 보인다.
그리고 하나 의심되는 곳이
x=0 인 곳인데
지금 x축이 딱 극댓값을 지나는 순간을 보고 있는것이므로
x=0에서 극댓값을 가지고
따라서 x=0 에서 저 그래프의 기울기는 0이다.
따라서 미분가능하다.
따라서 이때는 (나) 조건도 성립하고
따라서 이때 p=1, q=7 이라서
1+7=8 답은 3번이다.
3. x축이 극댓값과 극솟값 사이에 있는 경우
여기서도 g(x)를 그려보자.
일단 여기서도 두가지로 나뉜다.
ㄱ. 극댓값이 x>0 에 있는경우
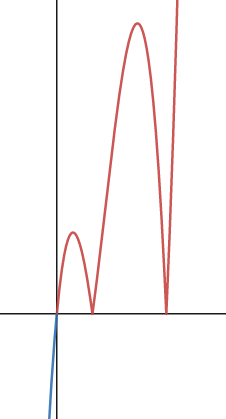
이런 g(x) 그래프가 얻어진다.
미분불가능점은 2개고 (나) 조건이 성립하지 않는다.
따라서 이건 탈락
ㄴ. 극댓값이 x<0에 있는경우
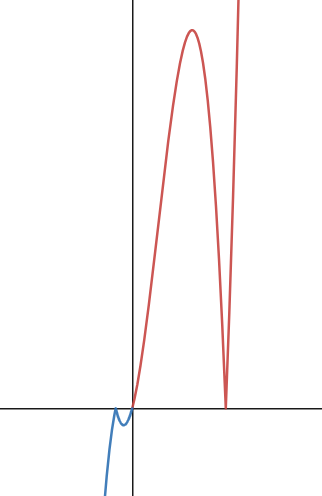
이런 g(x) 그래프가 얻어진다.
미분불가능점은 2개고 따라서 (나) 조건이 성립하지 않는다.
따라서 이건 탈락
4. x축이 딱 극솟값에 있는 경우
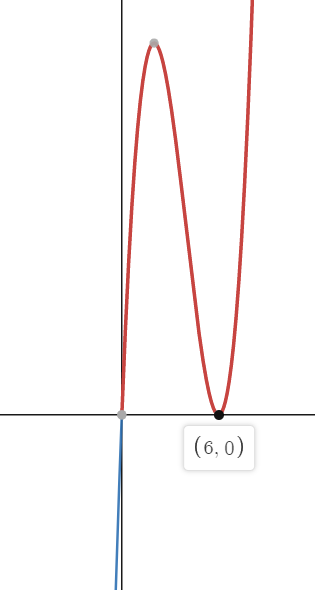
이런 g(x) 그래프가 얻어진다.
x=6 인 곳은 y=0이고 극소점이기 때문에
미분가능하다.
따라서 미분불가능점이 0개가 되고 조건에 맞지 않는다.
따라서 탈락
5. x축이 극솟값보다 아래에 있는 경우

g(x)는 이런 그래프가 얻어지고
당연히 미분불가능점은 0개이다.
따라서 탈락
따라서 x축이 딱 극댓값에 있는 경우만 가능하고
그에 따른 p,q 는 1, 7이므로 1+7=8
답은 3번
15 )

우선 저 방정식을 만족하는 해는
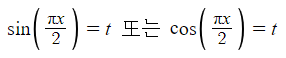
를 만족하는 해이다.
sin cos 각각의 그래프를 그려놓고
필요할때마다 쓰겠다.
검은 점 부분은
x<4 라서 x=4에선 함숫값이 존재하지 않는다는 표시이다.
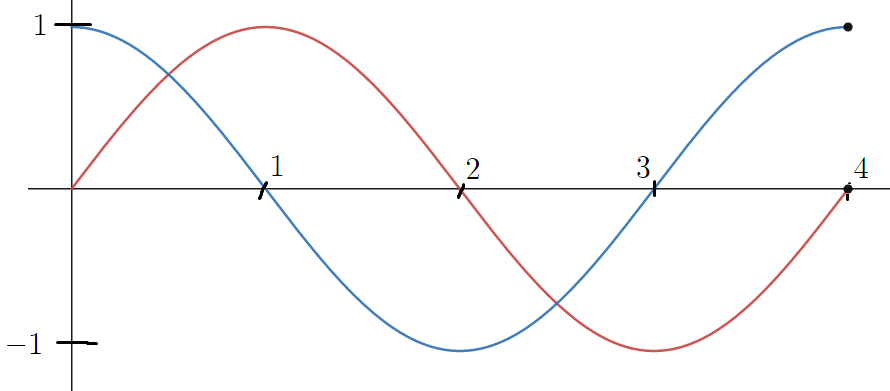
ㄱ )
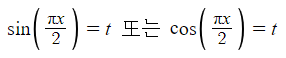
이건 다른말로

따라서 -1 ≤ t < 0 일때 y=t 를 그리면
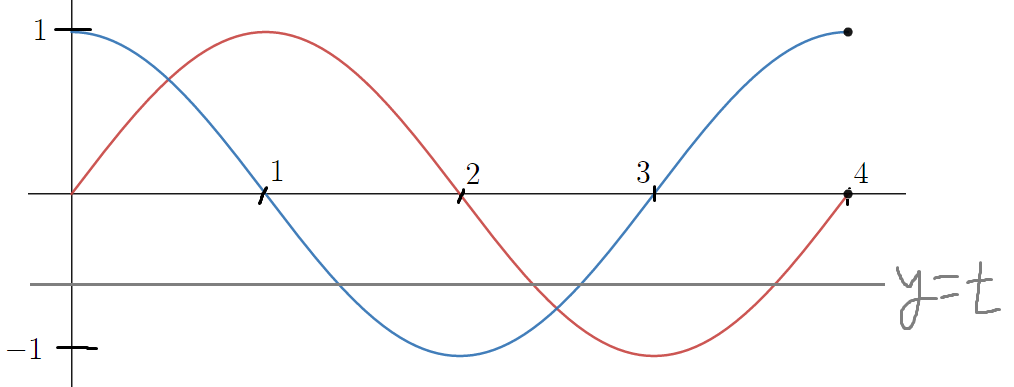
이정도가 될텐데
여기서 α(t)는 이걸 만족하는 해 중 가장 작은 값이고
β(t)는 이걸 만족하는 해 중 가장 큰 값이다.
여기서 핵심은
α(t)는 무조건 cos 그래프의 해이고
β(t)는 무조건 sin 그래프의 해이다.
기본적으로 cos 그래프는
sin 그래프를 평행이동한것과 모양이 똑같으니까
근데 저 범위 내에서는 cos 그래프가
sin 그래프보다 왼쪽에 위치하니까
당연히 최솟값은 cos 위에 있고
최댓값은 sin 위에 있는것이다.
그리고 여기서
sin 그래프의 값과 cos 그래프의 값이 같아지는 곳이 대칭점이고
그곳은 x=2.5니까
α(t)와 β(t)는 2.5 를 기준으로 대칭이다.
즉 α(t)와 β(t)의 평균이 2.5다.
따라서 ( α(t)+β(t) ) / 2 = 2.5 이고
따라서 α(t)+β(t)=5
따라서 ㄱ(o)
ㄴ )

우선 β(0) - α(0)을 구해보면
β(0) = 3 ( x<4 이므로 x=4에서의 함숫값은 정의되지 않는다. )
α(0) = 0
따라서 β(0) - α(0) = 3
다음으로 좌변을 구해보자.
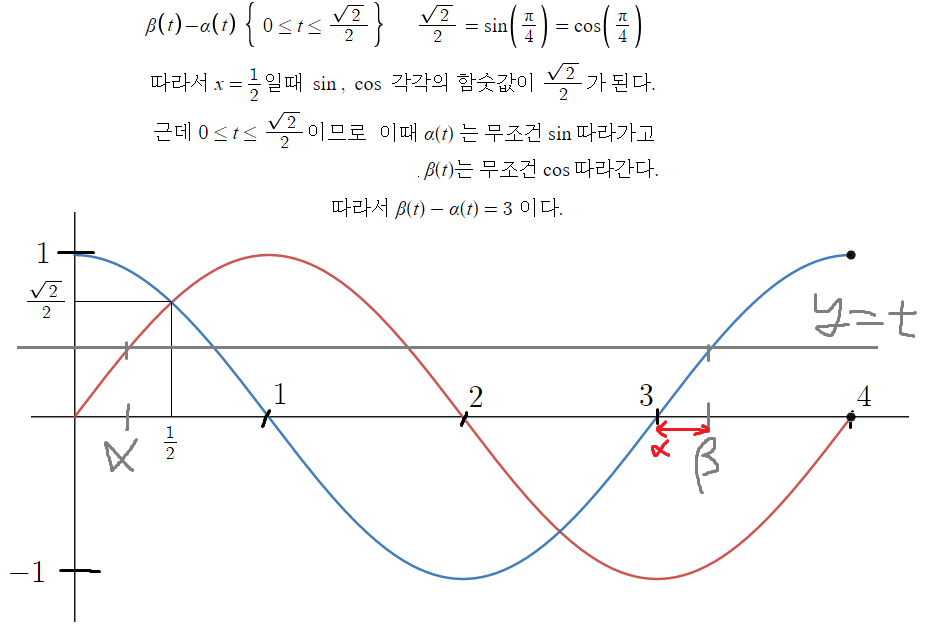
따라서 ㄴ(o)
ㄷ )
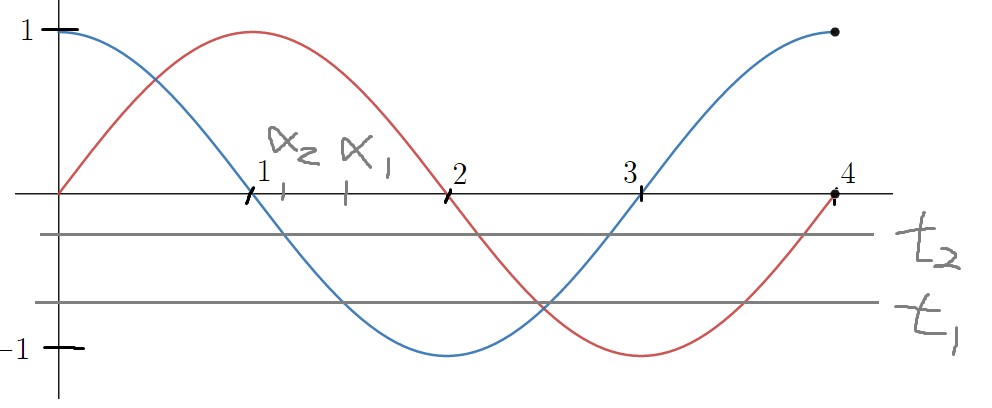
일단 t가 음수일때는 그림과 같이 성립할수 없다.
t₁과 t₂는 다른데 둘다 cos을 따라가기 때문이다.
물론 둘중 하나가 양수여도 성립할수 없다.
둘중 하나가 양수면 하나는 sin 따라가서 무조건 1보다 작은데
음수인게 cos 따라가면서 무조건 1보다 클것이다.
따라서 둘다 양수이고
만족할 조건은
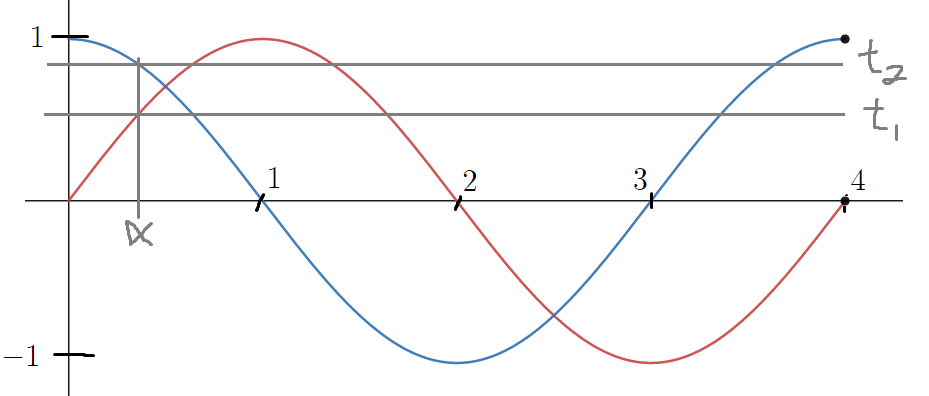
이런 식으로
둘다 양수이면서
하나는 sin에 걸치고
하나는 cos에 걸쳐줘야 가능하다.
그리고 t₂ - t₁ = 1/2 를 만족해야한다.
그림을 보면 α(t₂)는 cos 위에있고
α(t₁)은 sin 위에있다.

따라서 ㄷ(x)
따라서 답은 2번
'2022학년도 기출 해설 > 2022학년도 6월 모의평가 해설' 카테고리의 다른 글
| 2022학년도 6월 모의평가 수학 확률과통계 23번~30번 해설 (0) | 2021.12.26 |
|---|---|
| 2022학년도 6월 모의평가 물리II 해설 (0) | 2021.09.01 |
| 2022학년도 6월 모의평가 물리I 해설 (0) | 2021.08.31 |
| 2022학년도 6월 모의평가 수학 미적분 23번~30번 해설 (0) | 2021.08.31 |
| 2022학년도 6월 모의평가 수학 공통 16번~22번 해설 (0) | 2021.08.30 |



