
- 개요 -
함수는 함수인데 좀 특이한 함수들을 몇가지 소개해주고
함수의 그래프를 그리는 방법도 다룰것이다.
함수도 설명했고 그래프도 설명했으니
이제부턴 문제에서 f g x y a b 이런 문자들과
이상하게생긴 함수의 그래프들이
당연하다는듯이 등장한다.
- 서로 같은 함수 -
말 그대로, 두 함수가 똑같을 조건을 다루는것이다.
두 함수의 이름을 각각 f, g 라고 하겠다.
두번째 함수의 이름이 g인 이유는
그냥 f 다음으로 오는 알파벳이 g라서 그렇다.
f = g 면 서로 같은 함수이다.
너무 당연한거 아닌가?
이런걸 왜다루는가?
f와 g의 식이 다르게 생겼어도,
서로 같은 함수가 될 수 있다.
무슨 말이냐면,
f(x) = x 이고
g(x) = 1/x 라고 해보자.
일반적으로는 f(x)와 g(x)가 같지 않지만,
정의역을 어떻게 잡냐에 따라서 같아질수도 있다.
예를 들어, 정의역을 {-1, 1} 로 잡으면?
f(-1) = -1 이고, g(-1) = -1 이므로
f(-1) = g(-1) 이다.
f(1) = 1 이고, g(1) = 1 이므로
f(1) = g(1) 이다.
정의역 안에서 f와 g의 함숫값이 같으므로
f와 g는 같은 함수이다.
즉, 함수 식이 달라도
정의역이 어떻게 되느냐에 따라서
같은 함수가 될 수도 있다.
물론 식이 같으면 당연히 같은 함수이다.
문제를 하나만 풀어보면 감을 잡는다.

우선 f(x)와 g(x)의 함수 식이 다르기때문에
저 정의역에서의 함숫값들을 전부 비교해봐야한다.
f(-1) = g(-1) = 1
f(0) = g(0) = 0
f(1) = g(1) = 1
정의역 안에서 함숫값이 전부 같기때문에
f와 g는 서로 같은 함수이다.
그럼 이건?

이럴때는 서로 같은함수가 아니다.
왜냐하면, 서로 같은함수려면
정의역 내에서 함숫값이 전부 같아야한다.
그러니까, -1과 1 사이에있는 어떤 값을 대입해도 둘의 함숫값이 같아야한다.
x=0.5 만 대입해봐도 그렇지 않음을 알 수 있다.
따라서, 이런 결론을 얻는다.
보통은 함수 식이 다르면 서로 다른 함수이다.
대부분의 함수는 정의역이 위 문제처럼 범위로 주어지기 때문이다.
하지만, 정의역을 잘 잡아주면, 서로 같은 함수가 될수도 있다.
서로 같은 함수라고 무조건 식 자체가 항등식처럼 똑같은건 아니니
오개념에 주의하자.
- 상수함수 -
이것도 말 그대로이다.
함숫값이 상수인 함수를 상수함수라 한다.

예를 들자면, f(x)=1 이런게 상수함수이다.
상수함수의 뜻 자체는 쉽지만,
상수의 뜻은 확실히 알고갈 필요가 있다.
상수 : 값이 변하지 않는 수.
여기서 조심할건, 그냥 f(x) = c 라고 쓰면
상수함수라고 보장할 수 없다.
c가 x에 따라 변하는 수일수도 있다.
그래서 난 저기다가 아래로 한줄 추가해서
c는 상수라는 말을 추가로 써준것이다.
좀 덧붙이자면, c는 x에 대해서 상수이다. 라고 써야된다.
예를 들자면 ) 0, 1, π, ⅰ
얘네는 절대 값이 변하지 않는 수들이므로 상수이다.
변수의 반댓말이 바로 상수이다.
상수가 영어로 constant 라서,
상수면 보통 c 라고 쓴다.
이런 쓸데없는걸 왜 배우나 싶겠지만,
함숫값이 항상 같다는것 자체로 수학적인 의미가 있다.
- 항등함수 -
어떤 값을 대입했을 때,
그 값이 그대로 함숫값으로 나오게 되는 함수를
항등함수라고 한다.
말은 좀 어려운데, 식으로 보면 쉽다.

얘도 당장은 이게 무슨 쓸데없는거냐고 느낄 수 있는데,
항등함수는, 나중에 배울 '역함수' 라는걸 정의할때
아주 중요하게 쓰이는 도구이므로, 꼭 알아가야한다.
예를 들어, f(x)가 항등함수라면,
f(3) = 3, f(4) = 4
f(7x+13) = 7x+13
이런식으로 가는것이다.
자기 자신이 함숫값으로 나오게 된다.
- 함수의 그래프 -
함수의 그래프를 그리는법을 다룰건데,
그리기 전에, 그래프가 뭔지부터 알고가자.
y = f(x) , 즉 y는 x에 대한 함수일 때,
함수 f(x) 의 그래프를 그려볼것이다.
함수 f(x)의 그래프라는건, 쉽게 말하면
f(x)가 나타내는 도형이다.
보통 '선'으로 그려진다.
수학(상)에서 자취의 방정식을 다뤘었다.
여기서 '그래프'가 바로 '자취'의 일종이다.
특정 조건을 만족하는 점을 전부 모아서 도형으로 나타내는거다.
그리고 여기서는 보통 '선'으로 그려진다는거다.
그래프와 자취의 차이점은,
'원'은 자취이지만,
x값 하나에서 y값이 두개 나올수 있기때문에,
y에 대한 x의 함수는 아니다.
그래서 원을 함수의 그래프라 하지는 않는다.
x값이 있으면, 그것에 대응되는 f(x), 즉 y값이 있을것이다.
이걸 점으로 찍으면, 좌표는 (x, y)가 될것이다.
근데, x는 변수기 때문에
x값이라는건 정말 수없이 많이 존재할것이다.
그리고 그것에 대응되는 y값 또한 수없이 많을것이다.
그래서 점을 수없이 많이 찍을 수 있다.
여기서, 이 점을 찍는다는 작업을
할수 있는 x값에다가 전부 해준다.
그러면, '점의 자취'로써, 선이 만들어질것이다.
그게바로 함수 f(x)의 그래프이다.
요약하자면, 점들의 좌표를 구해서 점들을 찍은다음,
그 점들을 이어주면 된다.
근데, x값이 수없이 많다면서 점을 하나하나 언제 찍나?
그래서 사실 완벽하게 그리라고는 요구하지 않는다.
사람이 손으로 그래프를 완벽하게 그려내는건 인간 능력 밖이다.
정확히 그리려면 컴퓨터를 이용해야한다.
그래서, 적당히 특별한 지점 몇군데만 점을 찍은다음 감으로 그린다.
그래서, 문제에서는 그래프를 그리는것을 다룰 때
항상 따라다니는 말이 있는데,
'개형' 이라는 말이다.
개형 : 대체적인 생김새
인간이 손으로 정확하게 그려내는건 불가능하니까
특징만 잡아서 대체적인 생김새만 그릴 수 있으면 되는거다.
예를 들자면, 일차함수의 그래프는 직선으로 그려진다.
그리고 y=ax+b에서 b가 바로 y절편이므로
대충 직선을 그린다음, y절편에다가 여기 값이 b입니다 라고 표시해주면 되는거다.
이차함수중에서 가장 간단한걸로 가져와서 같이 그래프를 그려보자.

x=0 일때 y=0 이다.
x=1 일때 y=1 이다.
x=2 일때 y=4 이다.
x=3 일때 y=9 이다.
x=-1 일때 y=1 이다.
x=-2 일때 y=4 이다.
x=-3 일때 y=9 이다.
이것들을 모두 점으로 찍으면
아래와 같이 된다.

이것들을 부드럽게 이어주면 그래프를 그릴수 있다.
물론 정확히 그리려면 x=0.5, x=0.1, x=0.01 이런식으로
아주 세분화해서 전부 구해봐야겠지만
그럴수는 없으니 일단 적당히 포물선모양 나오게 그려주자.
'함수의 그래프를 그리는 원리를 아는가?' 가 목적이지
컴퓨터처럼 정확하게 그려내는가? 가 아니라서
대충 그려도 된다.
아까도 말했지만, '개형' 즉 대체적인 생김새만 나타내면 된다.

이게 바로 y=x² 의 그래프의 '개형' 인것이다.
- 예제 -
1 )

f(2) + g(-1) = 5 에서,
f는 항등함수이므로,
f(x) = x 이고, f(2) = 2 이다.
따라서, g(-1) = 3 이다.
근데 g는 상수함수이므로,
g(x) = 3 이다.
따라서, f(5) + g(3) 의 값은
f(5) = 5 이고 g(3) = 3 이므로
5+3=8, 따라서 답은 8
2 )

절댓값 기호가 있는건 사실 심화내용인데,
절댓값이란게 뭔지, 그래프를 그리는 원리가 뭔지만 안다면
충분히 풀어낼 수 있다 생각해서 예제로 넣었다.
인간은 정확한 그래프를 손으로 그려낼수 없기때문에,
'개형'만 그릴 수 있으면 된다.
y = |f(x)| 라고 한다.
절댓값 기호는 벗기라고 있는것이다.
벗기는 방법은 수학(상)에서 다뤘었다.
절댓값 벗기는법 : 범위를 나눈다.
f(x) < 0 일때는, |f(x)| = -f(x) 이고
f(x) ≥ 0 일때는, |f(x)| = f(x) 이므로
범위를 나누면 절댓값을 벗겨낼 수 있다.
절댓값을 벗겼으니 그래프를 그려보자.
f(x)≥0 이면, y = f(x) 이다.
따라서, f(x)≥0 인 경우만 그려보면
개형은 아래와 같이 된다.
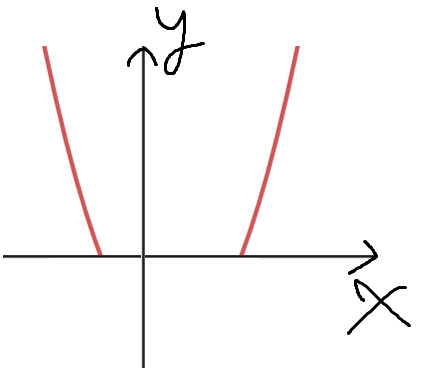
이제 f(x)<0 인 경우만 그리면 된다.
f(x)<0 이면, y = -f(x) 이다.
y = f(x)를 x축에 대해 대칭이동 한것이다.
이게 이해가 안되면, 수학(상)의 개념이 부족하다는거니까
이 블로그의 '점과 도형의 대칭이동' 글을 보자.
아무튼 y = -f(x) 일때는
y = f(x)의 그래프를 x축 대칭이동한것을 그리면 되는것이다.
그냥 그대로 위로 접어올리면 된다.
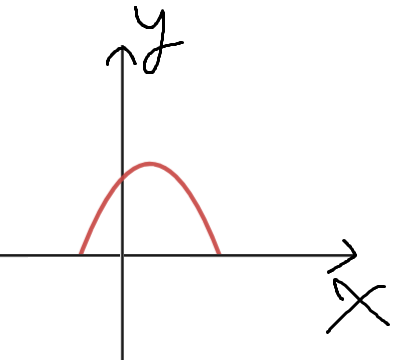
따라서, 최종적인 답은

대충 이렇게 그렸으면 정답이다.
내가 채점하는 사람이라면, 채점 기준은 이 두가지이다.
1. x축 아래로 내려가면 안되며,
2. 저렇게 x축을 맞고 튕겨나오듯이 그려야한다.
'수학(하) > II. 함수' 카테고리의 다른 글
| 함수 #6 - 합성함수 (0) | 2022.07.10 |
|---|---|
| 함수 #5 - 무리함수 (0) | 2022.07.07 |
| 함수 #4 - 유리함수 (0) | 2022.07.04 |
| 함수 #3 - 유리식 (0) | 2022.06.09 |
| 함수 #1 - 함수란 무엇인가? (0) | 2022.06.01 |



