
혹시 본인이 못 푼 문제인데
어떻게 푸는건지 궁금해서 이 글을 보는거라면
이 글을 보지 말것.
남이 풀어주는걸로는 실력이 늘지 않는다.
풀긴 풀었는데 풀면서 100%확신하진 못하고 약간 찜찜했거나
다른 풀이도 있을까 해서 찾아보는거라면
매우 환영이다.
원하시는 문제로 바로 가고싶으면
N번 문제로 가고싶다면
N )
이 형태로 검색하시면 됩니다.
예를들어 17번 문제로 가고싶으면 17 )
쉬운건 빠르게 넘어가면서
비약 하나도 없이 풀어보겠습니다.
제 생각에 가장 출제자의 의도에 근접했다 생각한 풀이만 담았습니다.
1 )

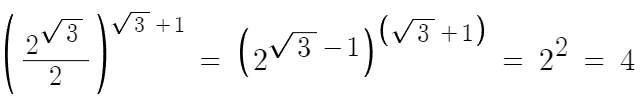
답은 4번
2 )

미분계수의 정의다. f'(2) 의 값을 구하는 문제이다.
f'(x) = 4x, f'(2)=8
따라서 답은 1번
3 )

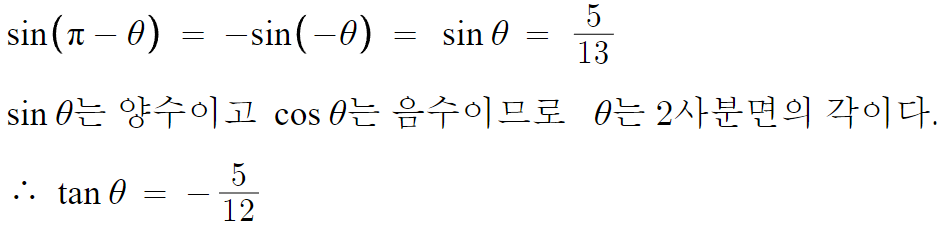
부호 주의. 답은 2번
4 )

일단 x<a 에서와 x>a 에서 모두 일차함수이므로
연결지점을 제외한 나머지 모든 부분은 연속이 될 수 밖에 없으니
연결지점인 x=a 에서만 연속이면 된다.
좌극한은 -2x+a 에 x=a 대입하면 -a
우극한은 ax-6에 x=a 대입하면 a²-6
함숫값은 f(a) 이고 -2x+a에 대입하면 -a
연속이려면 a²-6=-a 이어야 하고, 정리하면
a²+a-6 = 0 이다.
판별식 쓰면 D=25>0 이므로 상수 a값은 두 개 나온다.
따라서 근과 계수의 관계에 의해, a값의 합은 -1 이다.
따라서 답은 1번
5 )

일단 바로 길이 보이는 오른쪽 식부터 쓸것이다.
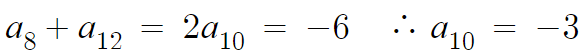
따라서 10번째항의 값은 -3이다.
따라서, 첫째항을 a라 하고 공차를 d라 하면
a+9d = -3 이다.
미지수가 2개니 관계식을 2개 써서 연립하면 될것이고
아직 안 쓴 식인 왼쪽 식을 쓰면 된다.
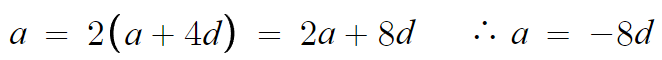
a=-8d 인데 a+9d=-3 이므로, 연립하면
d=-3, a=24 임을 알 수 있다.
따라서, 문제에서 요구하는 두번째 항의 값은
a+d = (24)+(-3) = 21
따라서 답은 3번
6 )

삼차함수가 극댓값을 가진다는 말은
극솟값도 가지며, 두 개의 극점에서 기울기가 0이 된다는 뜻이다.
따라서, f'(x)=0 이 되는 두 지점이 바로 극점이다.
f'(x) = 3x²-6x = 3x(x-2)
따라서, x=0 에서 극대, x=2 에서 극소를 가진다.
(최고차항의 계수가 양수이므로, 극대->극소 순서대로 극값을 가진다.)
따라서, f(0) = 9 이며,
따라서 k=9 이다.
여기까지 한걸 적으면,
f(x) = x³-3x²+9 이다.
극솟값 = f(2) = (8)-(12)+(9) = 5
따라서 답은 5번
7 )

이 문제는 어렵진 않으나,
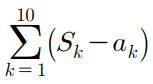
문제의 이런 생소한 표현때문에 당황했을 수 있는 문제이다.
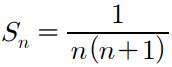
일단 이런 수열의 합을 계산하는건 많이 했던거고
이 식을 이용해서 계산하고 싶을것이다.
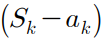
하지만 문제는 시그마 안에 있는게 S-a 라는 건데,
저걸 한번에 계산하려니 좀 복잡하다.
그래서, 덧셈식을 하나씩 풀어써볼거다.
어차피 10개밖에 안돼서 금방 한다.
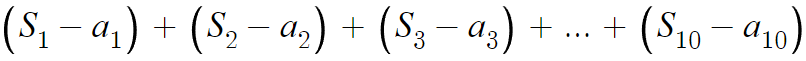
이런식으로 될텐데, 써보니 나름 간단하게 정리된다.
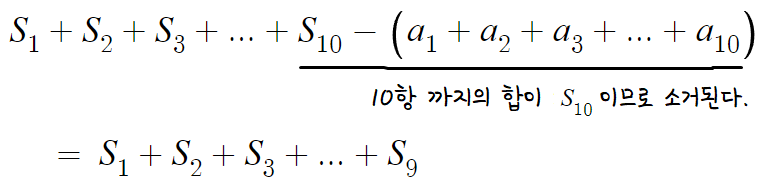
S의 일반항을 알고 있고, 아주 익숙한 형태이니 이제 마무리하면 된다.
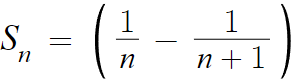
하던대로 부분분수 형태로 바꿔주고
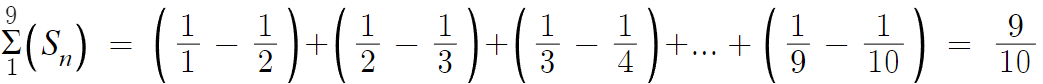
따라서 답은 5번
8 )

많이 풀어봤을 문제니 가볍게 넘어간다.
점 (1, 2) 에서의 접선을 작성한 뒤,
그 접선이 곧 곡선 y=x⁴+3x+a의 접선이 된다
라는걸 식으로 쓰면 a값이 나올것이다.
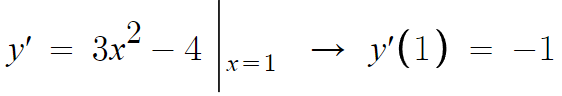
따라서, 접선의 기울기는 -1이며
(1, 2)를 지나므로, 접선의 방정식은
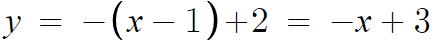
이제 이 직선이 y=x⁴+3x+a에 접할 조건만 써주면 된다.
접한다 = 접하는 지점에서 기울기가 같다
따라서, y=x⁴+3x+a 의 함숫값과 -x+3의 함숫값이 같을 때,
y=x⁴+3x+a 의 기울기는 -1 이다.

따라서, y=x⁴+3x+a 와 -x+3 에다 x=-1 대입하면
y(-1) = 1-3+a = a-2
-x+3 -> -(-1)+3 = 4
함숫값이 같으려면 a-2 = 4 이어야 하고,
따라서 a=6이다. 답은 1번
9 )


y=f(x)와 y=k 가 만나는 두 지점의 x좌표 차이는 8이다.
k값도 모르고 α값도 모르는 데다가,
구하려 해도 f(x)는 코사인함수라 연립 자체가 잘 안된다.
하지만 두 α값 사이의 관계는 안다.
그리고 f(x)와 g(x)도 식을 다 알려줬다.
그래서 이건 '식보단 그래프를 중점적으로 해석하는게 좋겠다'
라고 추론해볼 수 있다.
f(x)와 g(x)의 그래프를 그리면 아래와 같이 된다.
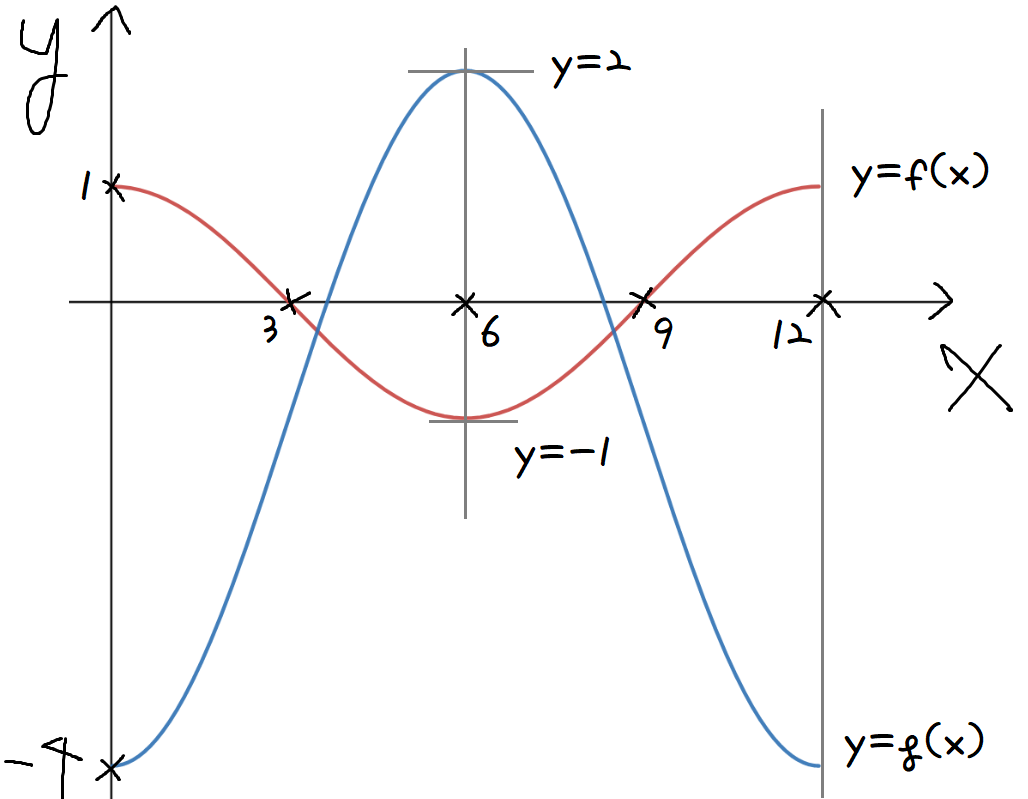

이제 그래프를 토대로 이걸 분석할건데,
f(x)의 그래프와 함수식을 보면
함숫값이 k가 되는 지점(함숫값이 같은 지점)은
x=6 을 기준으로 좌우대칭 이 되는곳에 있을수밖에 없다.
왜냐면 f(x)는 코사인함수라서 x=6을 기준으로 대칭이기 때문이다.
증명을 간단히 해보자면, x=6 을 f(x)에 대입해보면
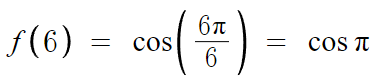
이번엔 x=6을 기준으로 해서
6+x 와 6-x 를 f(x)에 대입해보면

따라서 이런 결론을 또 얻는다.
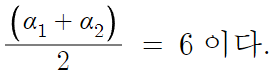
α₁ > α₂ 라 하면,
연립해서 α₁과 α₂ 의 값을 전부 알아낼 수 있다.
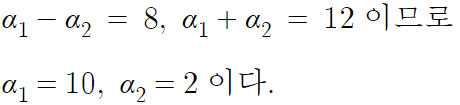
그럼 이제 f(2) = f(10) = k 인거니까, k값도 알아낼 수 잇다.
이 k값을 토대로 β값까지 알아내서 마무리하면 된다.
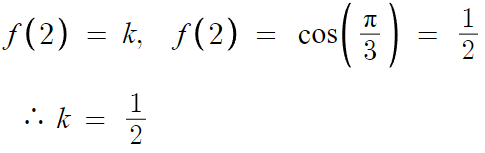
따라서 k = 1/2 이다.
이제 g(β) = k = 1/2 이라는 방정식에 대입해서 계산하면 끝
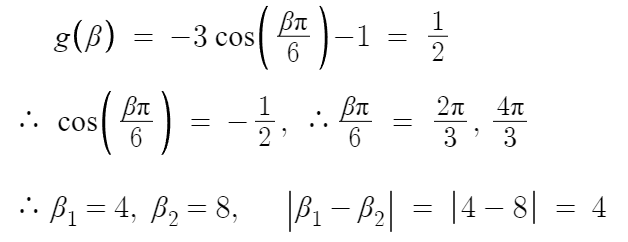
따라서 답은 3번
추가로, y=k 의 그래프까지 그린 뒤
그래프의 모양을 보고 분석하는것도 좋은 풀이 방법이다.
10 )

속도, 거리에 대한 기본 문제이다.
우선 점 P의 위치부터 알아야하니
시각 t=2 에서의 점 P의 위치부터 구해보자.

점 P(8+2a)와 점 A(6) 사이의 거리가 10이므로,
8+2a 와 6의 차이는 10이다.

따라서 답은 4번
11 )

이런 문제가 출제되면 꼭 사설스러웠다? 내신스러웠다?
이런 평가가 커뮤니티에 돌아다니던데
혹시 이거 틀렸다면, 출제를 이상하게 했다고 남탓하기보단
'이런식으로도 낼 수 있으니 전부 대비해야 되겠구나' 라는 자세가 중요하다.
학생 입장에서 문제를 평가해봤자
이미 치룬 시험의 결과는 절대 변하지 않는다.
그리고 풀지 못했다는것 그 자체로 깊이 반성해야할 일이다.
이 문제가 수능에 출제되지 않았음에 안도하고,
이 문제를 틀렸음에 반성하고
다음에 이런 문제가 나오면 풀 수 있도록 연습하고
수학 실력은 그렇게 늘리는것이다.
아무튼 문제풀이
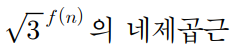
우선 이 말부터 해석을 잘해야한다.
저게 무슨 말인가?
저걸 식으로 그대로 옮겨쓰자면, 이 말이다.


따라서 이 문장은, 저 방정식의 실근의 곱이 -9라는 뜻이다.
우선 좀 방정식을 쉽게 풀기 위해 식을 보기쉽게 하자면
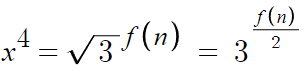
그리고, 이 방정식의 실근을 구해주면
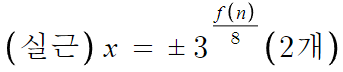
이제 두 실근의 곱을 구해주면
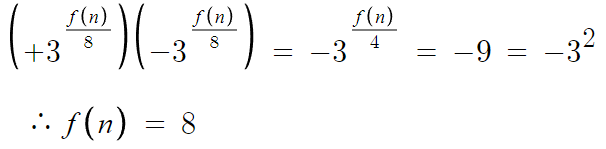
따라서, 이런 결론을 얻는다.

이제 f(x)의 식을 어느정도 알고있으니
아까 얻은 결론과 적절히 융합하면 답을 얻을 수 있을것이다.
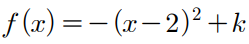
f(x)는 (2, k)를 꼭짓점으로 하고
최고차항의 계수가 -1인 이차함수이다.
일단 아는 대로 그려보자.
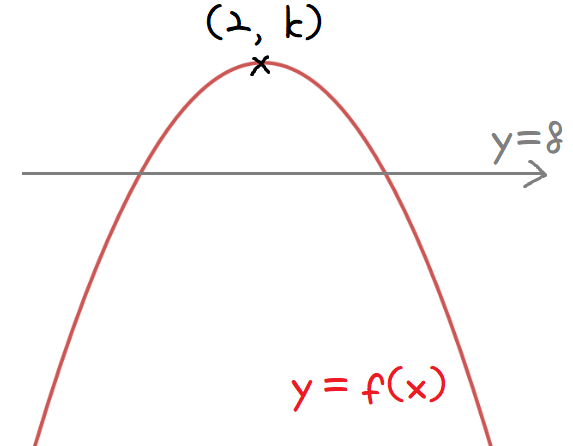
f(n)=8 의 자연수 실근이 2개 있어야 하니
y=8은 당연히 꼭짓점보단 아래에 있어야한다.
그런데, 그리자마자 실근이 될 수 밖에 없는 값을 찾았다.

파란색으로 표시된 부분은
f(n)=8 의 실근이며,
이 실근 n이 자연수로 존재해야한다.
그 실근은 그래프상 2보다 작아야 하므로,
여기서 가능한 자연수 n값은 1 뿐임을 알 수 있다.
따라서, f(1)=8 이다.
이제 대입해서 계산만 하면 마무리 될것이다.
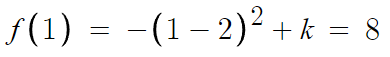
따라서 k=9
따라서 답은 2번
12 )

이 소재는 꽤 오랜만에 등장했다.
그냥 정직하게 풀면 어렵지 않다.
AH의 길이와 CH의 길이를 t로 표현하기만 하면 된다.
어차피 A, C, H는 y좌표가 같은 점이니
x좌표의 차이만 구하면 된다.
AH = A와 B의 x좌표 차이
A와 B의 의미는
y=x² 과 y=x+t 의 교점
즉 방정식 x² = x+t 의 실근
따라서, A와 B의 x좌표 차이라는건
방정식 x² = x+t 의 두 실근의 차이 이다.

AH 구했고, CH만 구하면 된다.
C는 A를 y축기준 대칭이동한 점이므로,
C의 x좌표는 -x₂ 이다.
따라서, CH의 길이는
(B의 x좌표) - (C의 x좌표)
B의 x좌표 = x₁ 이므로

마무리로 극한값 계산만 하면 된다.
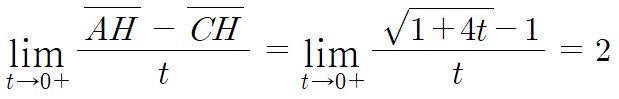
따라서 답은 2번
13 )

개인적으로 공통 객관식문제중 가장 어려웠던 문제
일단 문제에서 준 조건대로 표시해보겠다.
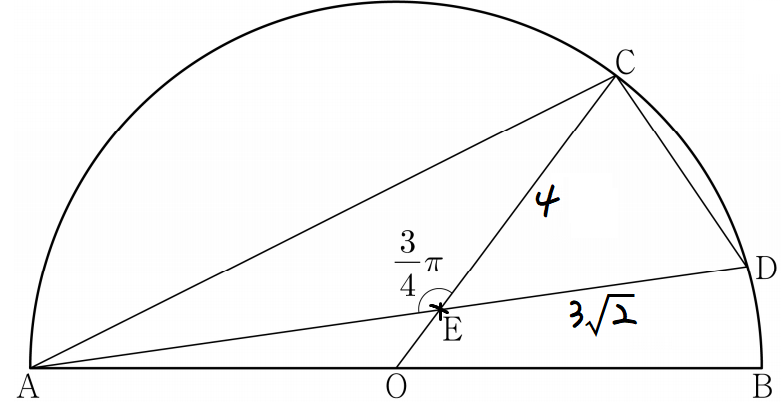
CD의 길이부터 구해볼것이다.
일단 삼각형 CDE를 보면, 두 변의 길이를 알고있으니
코사인 법칙을 적용하면 CD의 길이를 알아낼 수 있고, 각 하나만 알면 된다.
각 하나는 바로 보이는게, 각 CED는 π/4 임을 바로 알 수 있고,
이제 코사인법칙 적용하면 CD의 길이를 구할 수 있다.
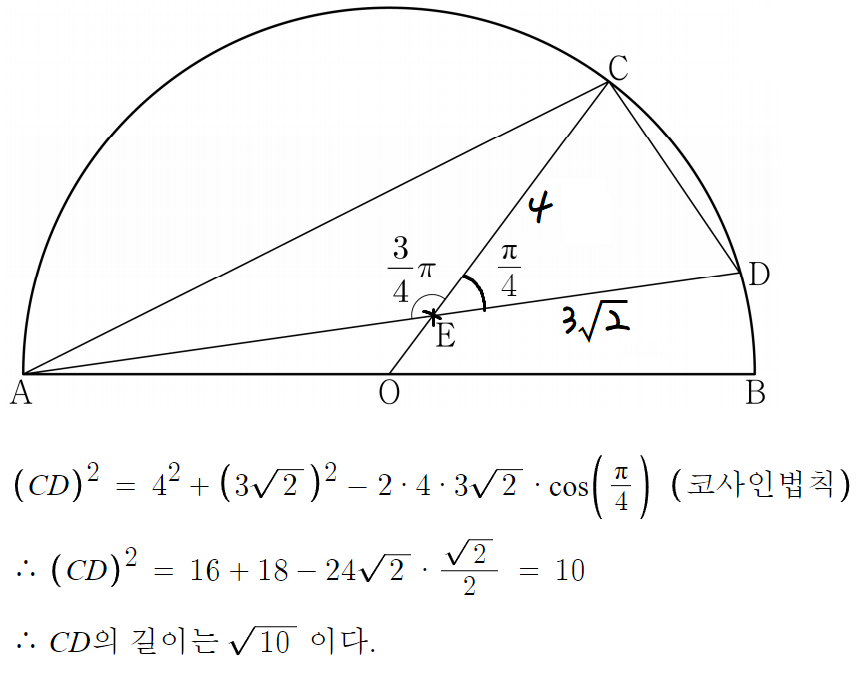
여기까지 한걸 표시하면
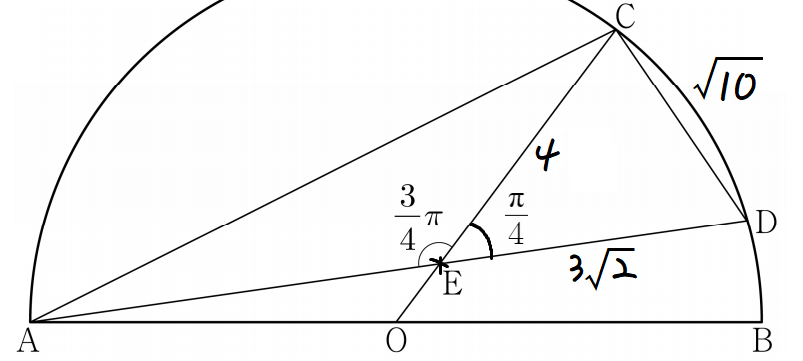
이제 AC의 길이만 구하면 되는데,
이 길이를 구하는게 상당히 어려웠다.
아마 이거 못풀었어도, 대부분 CD의 길이까지는 구했을것이다.
이 문제가 왜 어려웠냐면,
원의 반지름을 주지 않는 생소한 상황이다.
그리고 E도 원 위의 점이 아니고,
심지어 O도 원 위의 점이 아니기 때문에
원주각이나 이등변삼각형을 이용해 푼다거나 하는 풀이가 불가능하다.

이 원의 반지름을 구해볼것이다.
원의 반지름을 R이라 하겠다.
여기서 반지름에 대한 관계식을 세우려면,
보조선 하나를 그어야한다.
O에서 D로 보조선을 그으면
삼각형 OED가 만들어진다.
OD의 길이는 R이며,
OE의 길이는 R-4 이다.
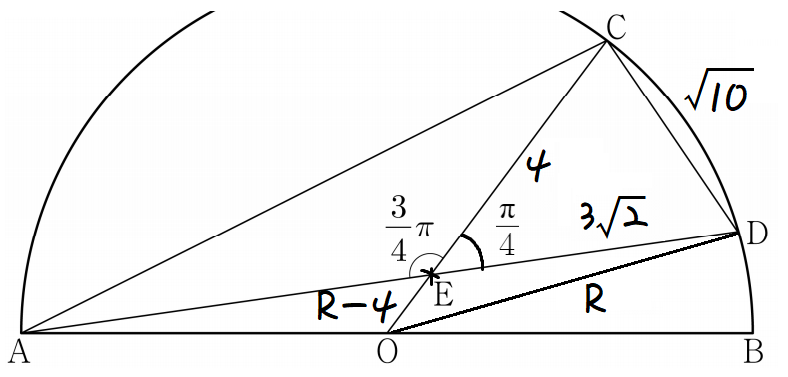
세 변의 길이를 R에 대해 나타냈고,
∠OED = 3π/4(맞꼭지각) 임을 알고있기 때문에
삼각형 OED에 대해서 코사인법칙을 적용하면
R에 대한 방정식이 나올테니, R값을 알아낼 수 있다.

따라서 R=5 이다.

이제 AC의 길이를 알아내야 하는데,
저 원은 삼각형 ACD의 외접원이고
외접원의 반지름이 5라는걸 알고 있는데,
외접원의 반지름과 내접 삼각형의 관계? 사인법칙밖에 없다.
삼각형 ACD에다가 사인법칙을 적용해서 엮어보고 싶다.
하지만, 삼각형 ACD는 각을 아는게 없다.
따라서, 알고있는 다른 도형의 정보를 이용해 간접적으로 sin값을 알아내야한다.
삼각형 ACD의 세 내각중에서
다른 도형과 엮어볼 수 있는 각은
∠ADC 이다.
∠ADC는 삼각형 ADC의 내각이면서, 동시에 삼각형 CDE의 내각이기 때문이다.
즉, ∠ADC = ∠CDE 이다.
삼각형 CDE에 대한 정보는 전부 알고있으니,
삼각형 CDE에서, ∠CDE에 대해 사인법칙을 적용하면
sin(∠CDE) 의 값을 알아낼 수 있을거고
∠ADC = ∠CDE 이므로
sin(∠CDE) = sin(∠ADC) 이다.
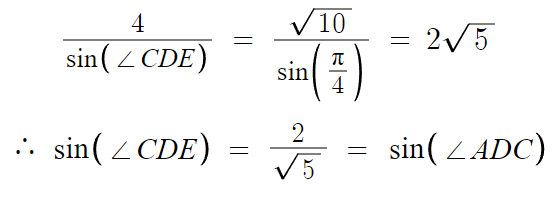
이제 삼각형 ADC에서, ∠ADC에 대해 사인법칙을 적용하면
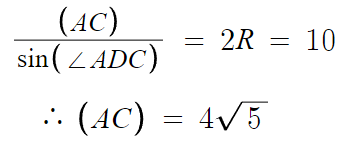
따라서 AC = 4√5 이고, 마무리계산하면
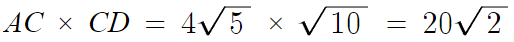
따라서 답은 5번
14 )

ㄱ )
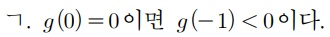
g(0)의 값을 줬으니
g(t) 에다가 t=0 을 대입해보는게 기본이다.
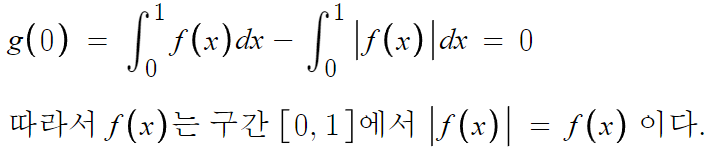

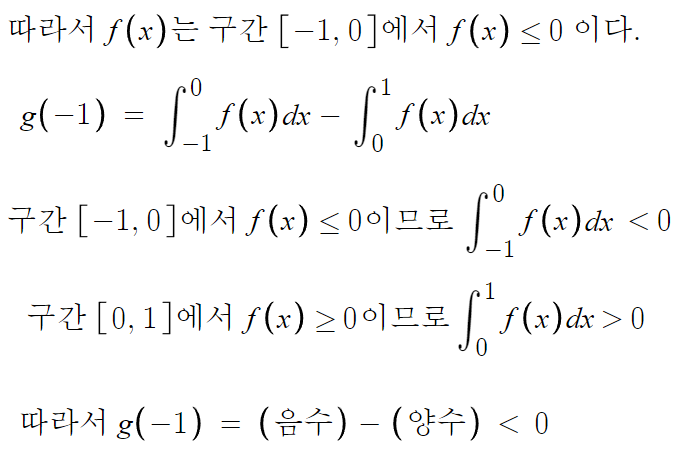
따라서 ㄱ(o)
ㄴ )
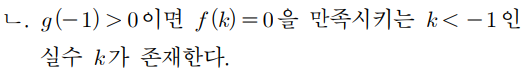
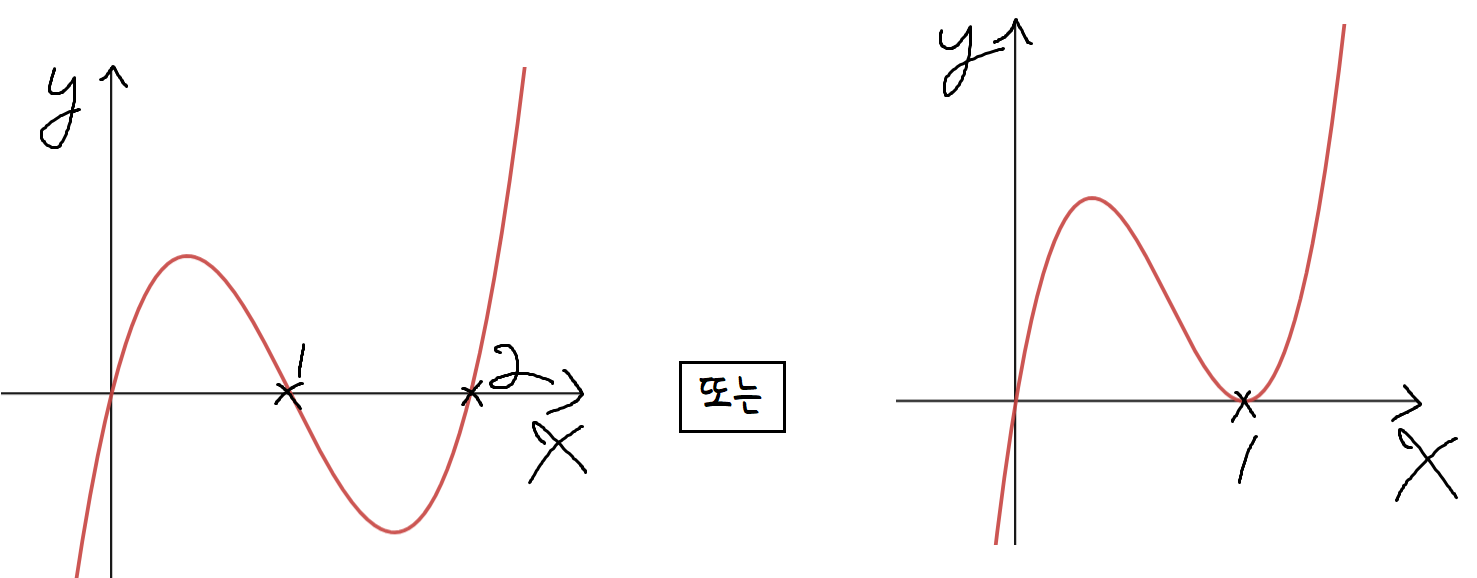
이건 아마 현장에서 시험본 학생들은 그래프로 풀었을거같은데,
그래프로 풀수도 있고 수식으로 풀수도 있으니
둘 다 보여주겠다.
물론 그래프와 수식 둘 중 하나만 쓰는것보단
적당히 필요에 따라 섞어가면서 풀어가는 센스가 필요하다.
1. 수식을 이용한 풀이(정석)
일단 하라는대로 대입해보고 정리하겠다.
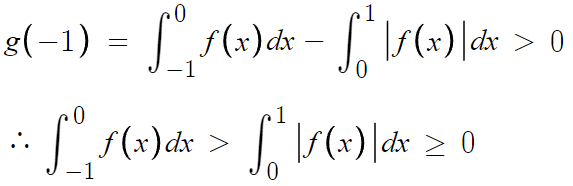


따라서 ㄴ(o)
2. 그래프를 이용한 풀이
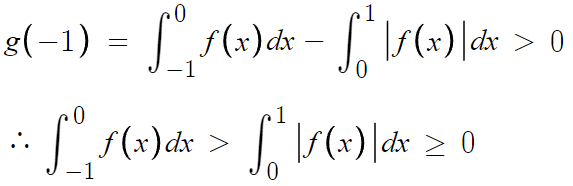
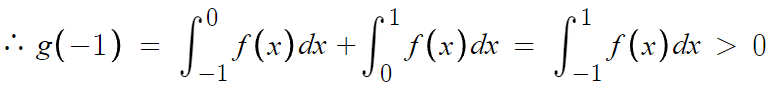
일단 여기까진 하던대로 한다.
이제 y=f(x)의 그래프가 x=0, x=1, x=k 에서 x축과 만나며,
-1부터 1까지의 정적분 값이 양수가 되도록
f(x)의 그래프를 적당히 정해주면 된다.
k값이 0이나 1이 될 수도 있으니 조심하자.
이건 해설이니 '답이 되지 못하는 경우' 도 포함해서 모두 꼼꼼히 해줄거지만,
실제 시험장이었다면 직관적으로 '문제에서 요구하는 상황일 가능성이 높은것'
을 판단해서 빠르고 정확하게 처리해야한다.
첫번째 : x축에 접하는경우
일단 x축에 접한다는 건,
x=0 이나 x=1 이 '중근'이 된다는거니
이 때 k=0 이거나 k=1 이다.
만약 k=0 이면 바로 모순이 발생한다.
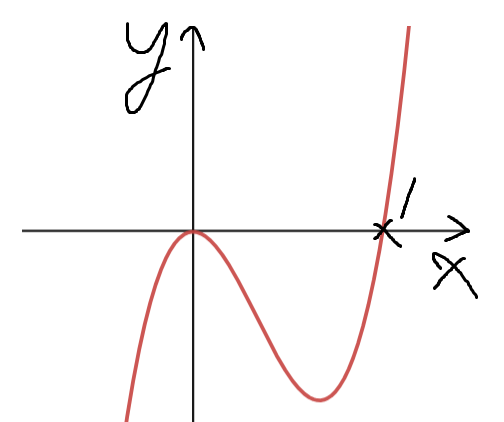
k=0 이면 y=f(x)의 그래프가 이렇게 생겼을거고
구간 [-1, 1] 에서 f(x)≤0 이므로, 정적분값은 절대 양수가 될 수 없다.
이번엔 k=1 이라면, y=f(x)의 그래프는
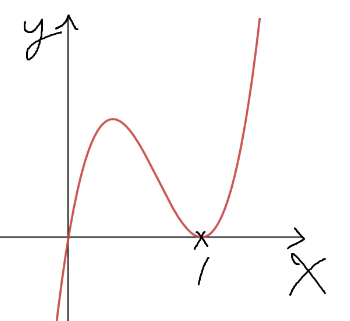
이 때 역시 정적분값이 양수가 될 수 없으므로 모순이 발생한다.
왜냐면, (0≤x≤1) 인 양수 x에 대하여
항상 f(x) < f(-x) 이기 때문이다.
즉, x<0 에서 f(x)가 내려가는 속도가
x>0 에서 f(x)가 올라가는 속도보다 항상 빠르므로,
정적분값은 결론적으로 음수가 될 수밖에 없는것이다.
결론은, y=f(x)가 x축에 접하는 경우는
ㄴ 선지에서 가정하는 상황 자체에 모순이므로,
이 경우는 생각하지 않아도 된다.
2. 1<k 인 경우
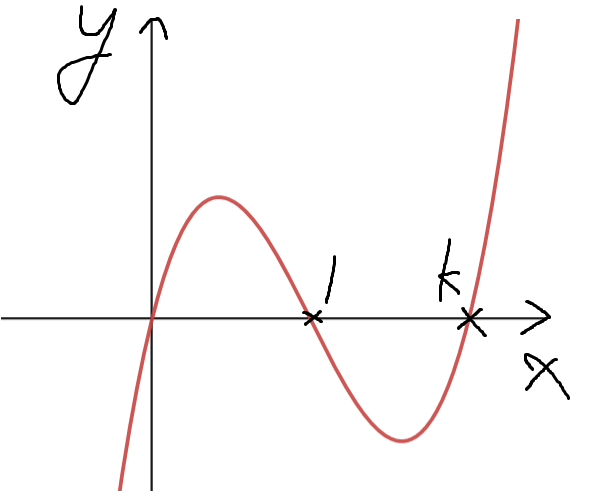
아까와 같은 논리로, 정적분값이 음수이므로 모순이 발생한다.
3. 0<k<1 인 경우
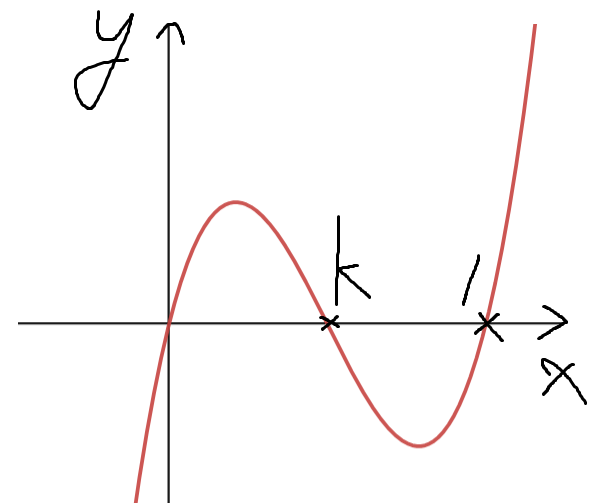
이것 역시 정적분값이 음수이므로 모순이 발생한다.
4. -1≤k<0 인 경우
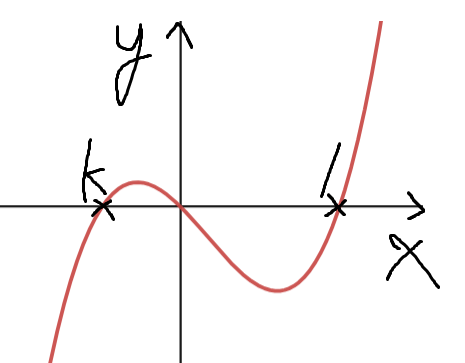
-1≤x≤k 에서 f(x)≤0 이므로,
-1부터 k까지의 정적분 값은 음수이다.
따라서 -1부터 1까지의 정적분 값이 양수이려면
k부터 1까지의 정적분 값이 양수여야한다.
하지만 저 상황에서는 '삼차함수의 대칭 중심점'이
x≥0, y≤0 에 있으므로,
k부터 1까지의 정적분 값은 양수가 될 수 없다.
따라서 이 상황 역시 모순이다.
남은 건 하나밖에 없으며, 이게 문제에서 요구하는 상황이다.
k<-1 이어야한다.
5. k<-1인 경우
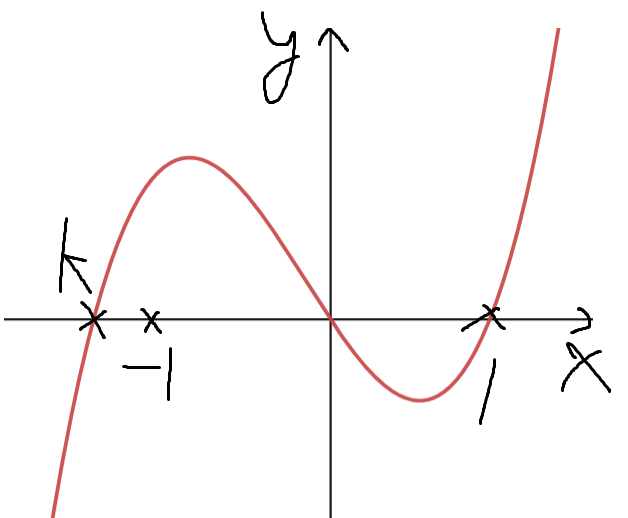
'삼차함수의 대칭 중심점'이 x<0, y>0 에 있고,
f(-1)>0, f(1)=0 이므로
-1부터 1까지 정적분하면 양수이다.
따라서 g(-1)>0 이면 f(k)=0 을 만족하는 실수 k가 k<-1에서 존재한다.
라는 명제는 참이다.
따라서 ㄴ(o)
ㄷ )

이건 단순히 음수, 양수를 판단하는게 아니라,
정확히 -1 이라는 값보다 작느냐고 물었으니
그래프만으로는 한계가 있고,
결국 식 써서 계산으로 처리해야하는 문제이다.
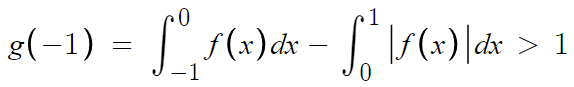
이게 문제 조건을 식으로 적은건데,
여기서 아까 ㄴ 선지에서 참임을 증명한 명제를 가져오자면
g(-1)>0 일 때, f(k)=0 을 만족하는 실수 k가 k<-1 에서 존재하므로,
f(x)의 식을 이렇게 작성할 수 있다.
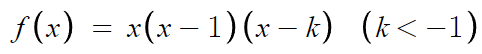
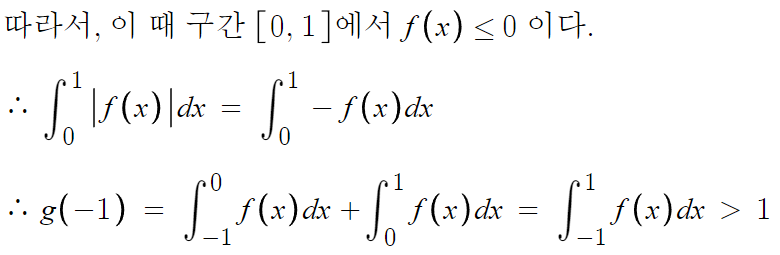
ㄴ 선지 풀때 썼던 방법을 그대로 적용할거고,
f(x) 작성했으니 정적분해서 값 비교만 해주면
k값의 범위가 나올거고
그걸 토대로 g(0)의 범위도 구할것이다.
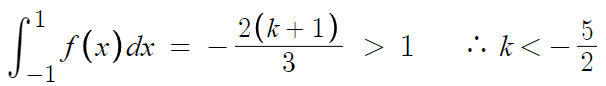
ㄴ 선지 풀 때 적은 식을, 우변 값만 바꿔서 활용하면 된다.
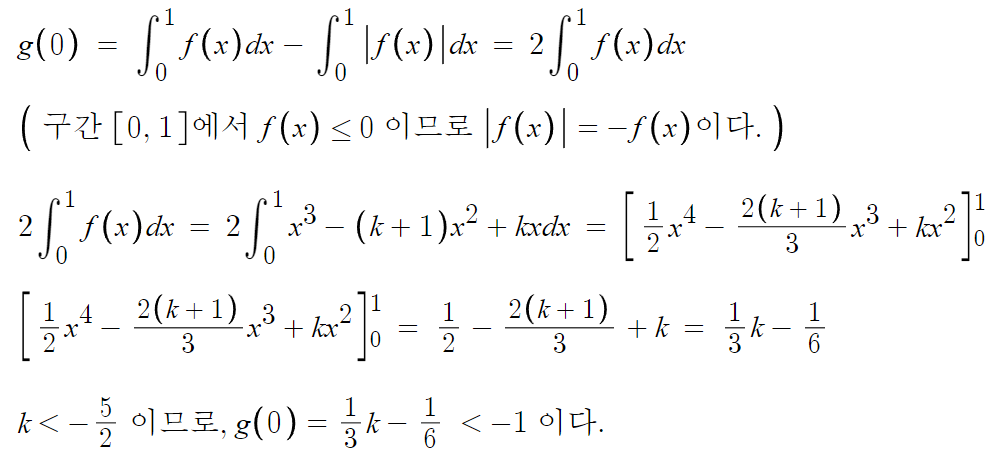
따라서 ㄷ(o)
따라서 답은 5번
15 )

크게 어렵지는 않은 문제였으나,
이 문제가 15번이라는 객관식 마지막문제로 왔으므로
이 문제를 시도할때면 이미 시험시간이 부족해서 침착하게 생각하기 어려웠을것
조건식의 생김새가 나름 복잡한것
이것들을 감안하면 충분히 객관식 킬러의 이름값을 하는 문제이다.

일단 이것부터 풀어보자.
저건 k에 대한 항등식이므로, k값에 아무거나 대입해도 무조건 성립한다.
일단 뭐하는 수열인지 잘 모르겠으니, k값을 하나씩 대입해보자.
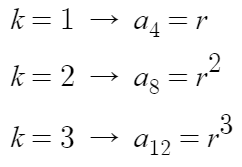
3개정도만 대입해봤다.
항의 간격이 4칸이지만, 나름 등비수열과 같은 모양이 나왔다.
r의 크기는 1보다 작으므로,
이 수열은 (4의배수) 번째 항마다 크기가 1보다 작은 항이 나온다.
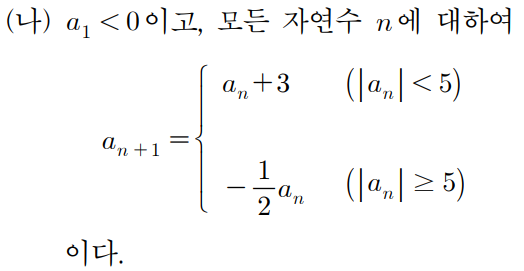
이제 이것도 해석해야되는데,
원래같았으면 첫째항 a₁부터 시작해서
n=1, n=2, ... 이런식으로 하나씩 대입해서 찾았겠지만
이건 a₁에 대한 정보가 너무 빈약하다.
하지만, a₄의 값은 r 이라는
크기가 1보다 작은 나름 구체적인 범위의 값으로 주었다.
따라서, 이 문제에서 수열을 분석할때는
a₁에서 출발하기보단, a₄에서 출발하는게 합리적이다.
a₄에서 a₁을 향해 거꾸로 추론하는거다. (역추적)
일단 a₄가 양수인지 음수인지는 모르겠으나,
양수인 경우와 음수인 경우를 나눠서 해보면
둘 중 하나는 문제 상황에 모순이 생길테니
두 가지로 경우를 나눠서 해보면 될것이다.
수열은 함수이므로, 함수의 그래프를 그리듯이
이 수열의 그래프를 그려보겠다.
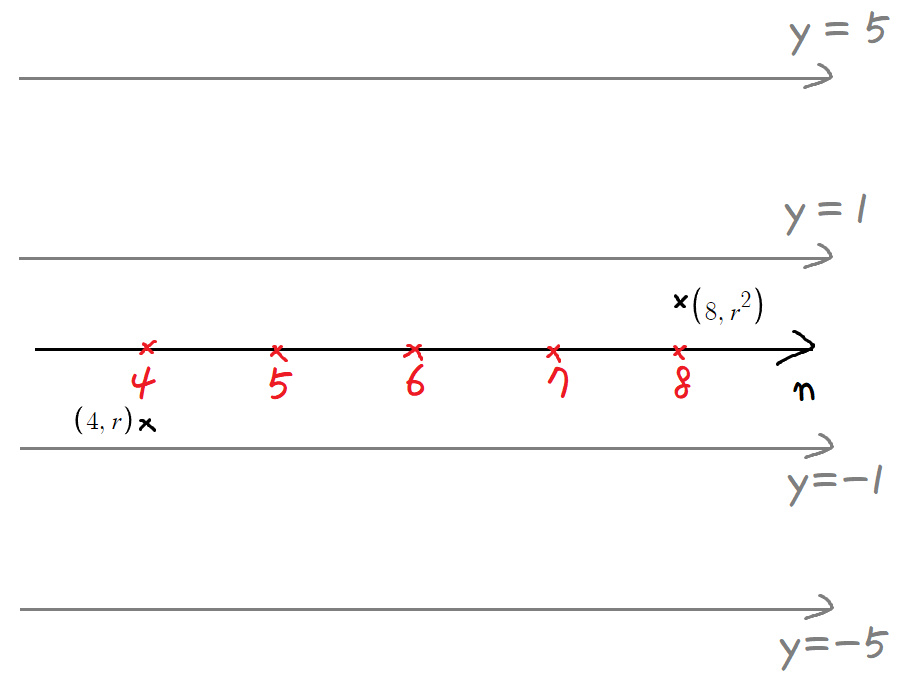
- a₄가 양수인경우(r>0) -
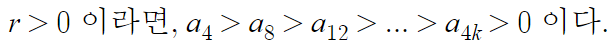
이를 토대로, 나름대로 그래프의 큰 틀을 잡아보면
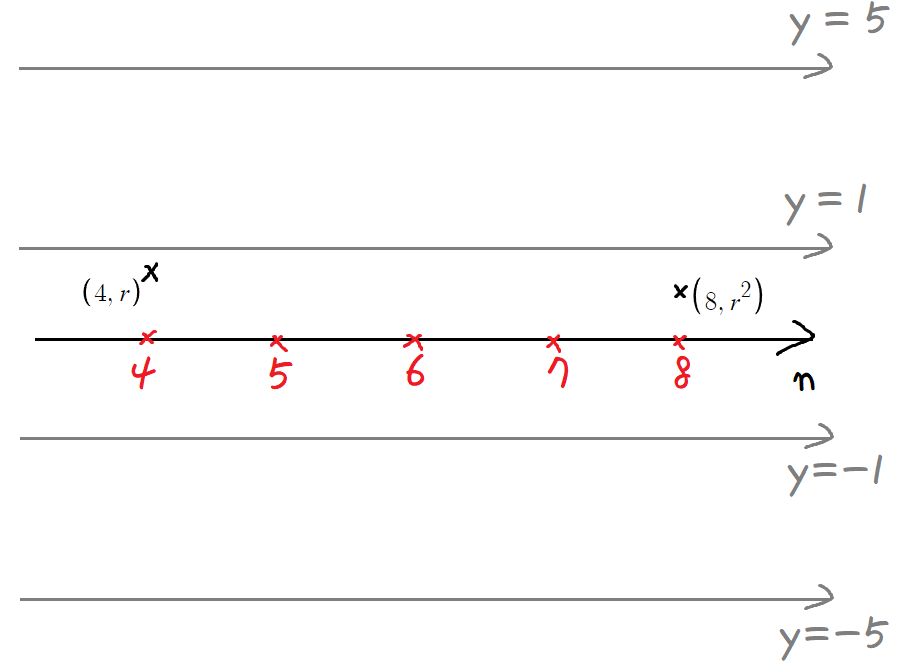
y=1과 y=-1은, r<1 임을 그래프로 표현하기 위해 추가한 선이고
y=5와 y=-5는, (나) 조건에 의하면 수열의 다음 항을 정할 때
현재 항의 크기가 5보다 큰지 작은지에 따라 양상이 달라지기 때문에 추가한 선이다.
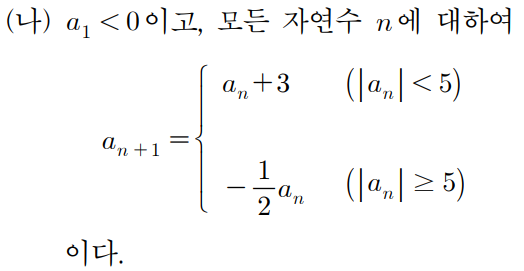
이 조건에 의하면, 4번째 항의 크기가 5보다 작으니
5번째 항은 r+3 이며, 3보다 크고 4보다 작을것이다.
6번째 항 또한, 5번째 항의 크기가 5보다 작으니
6번째 항은 r+6 이며, 6보다 클것이다.
여기까지를 그래프로 그리면
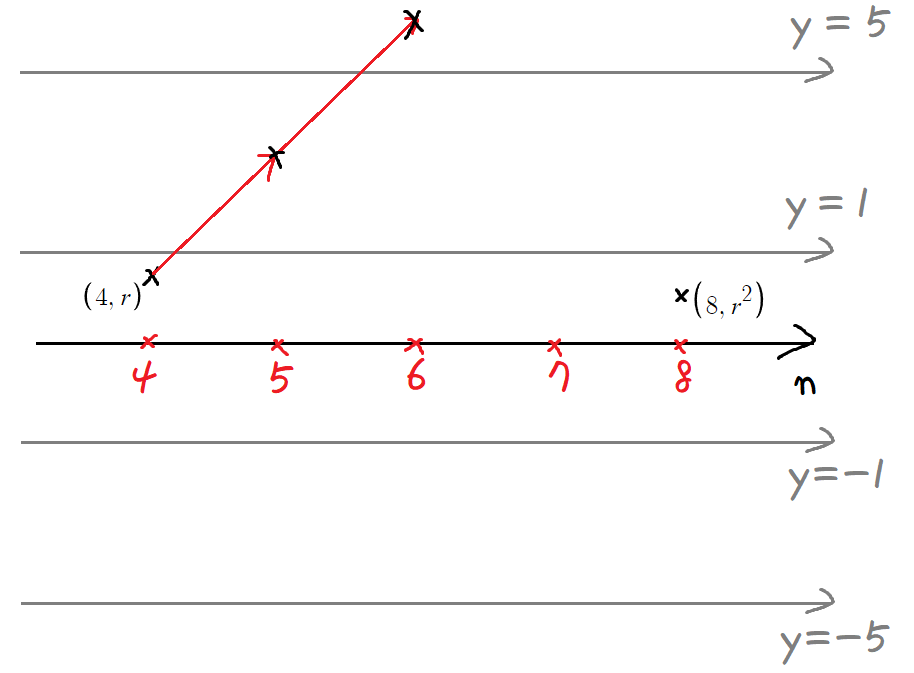
이제 8번째 항이 양수가 되어야 하는데,
우선 6번째 항의 크기가 5 이상이므로
7번째 항은 음수이다.
따라서, 그래프를 다 그려보자면 이렇게 생겨야한다.

꽤 그럴싸하다. 이제 r값을 계산해보겠다.
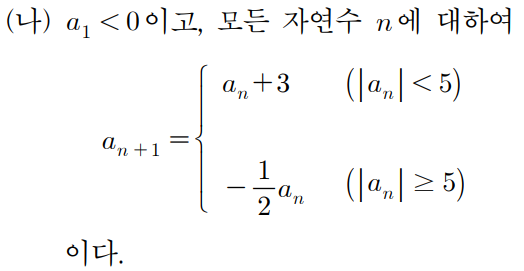
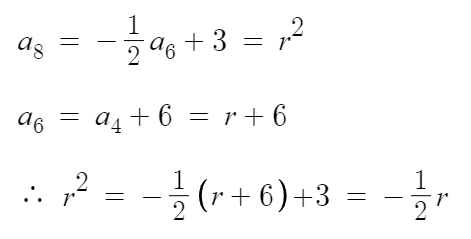
이를 만족하는 r값은 0 또는 -1/2 이며,
아까 가정했던 r>0 이라는 조건에 모순이다.
따라서, r>0 이면 모순이 생긴다는것을 알 수 있다.
따라서, r<0 이다.
- a₄가 음수인경우(r<0) (정답이 되는 상황) -
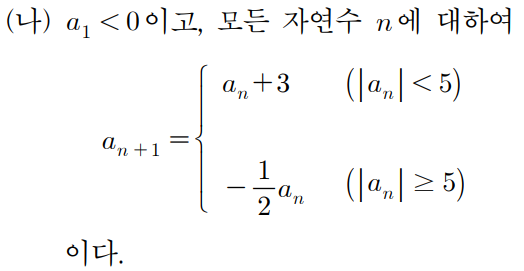
하던대로 하면 된다.
크기가 5보다 작으면, 3만큼 위로
크기가 5 이상이면, 뒤집고 크기 절반
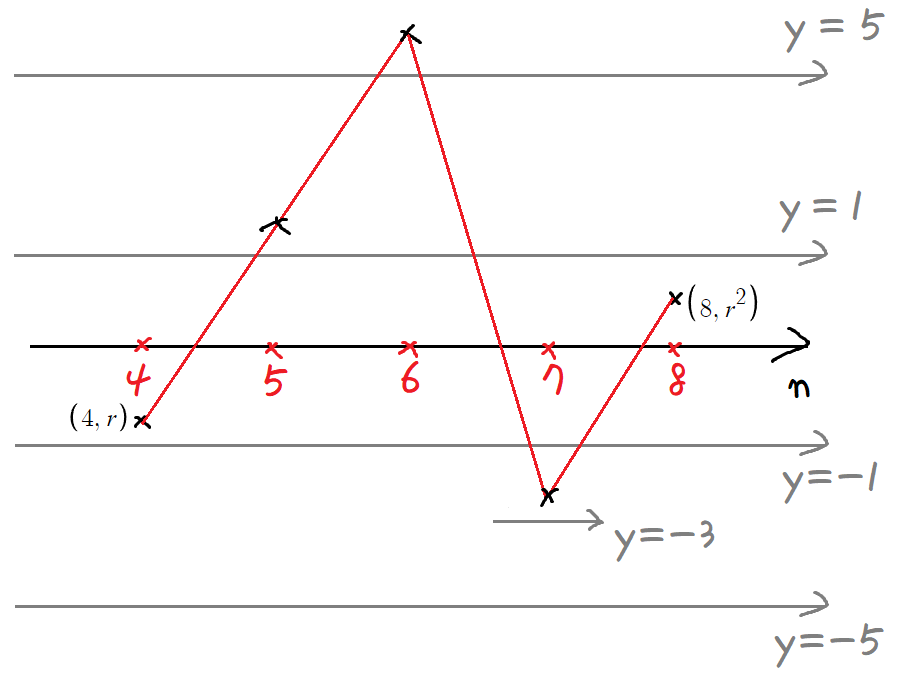
문제 상황에 딱 알맞는다.
r<0 임을 한번 더 확인한것이다.
이러면 좀 더 확신을 갖고 풀 수 있다.
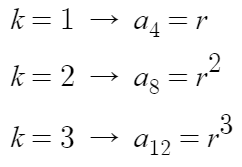
(가) 조건에 의하면 8번째 항은 r²인데,
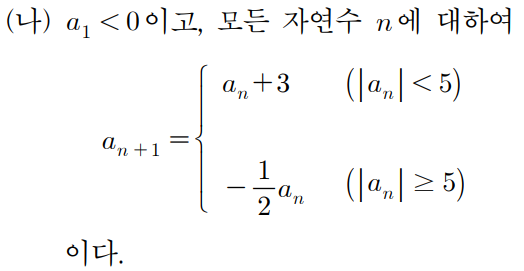
(나) 조건에 의하면 8번째 항은
5번째항 : r+3
6번째항 : r+6
7번째항 : -(r+6)/2
8번째항 : -(r+6)/2 + 3 = -r/2
(가)와 (나) 조건을 둘 다 만족해야 하므로,
r² = r/2 임을 알 수 있다.
r≠0 이므로, 이 방정식의 해는 r=-1/2 이다.
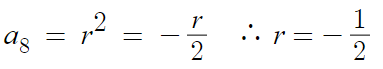
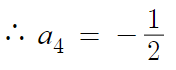
a₄ 의 값을 알았으니,
(나) 조건식에다 대입만 해보면 a₁값을 알아낼 수 있을것이다.
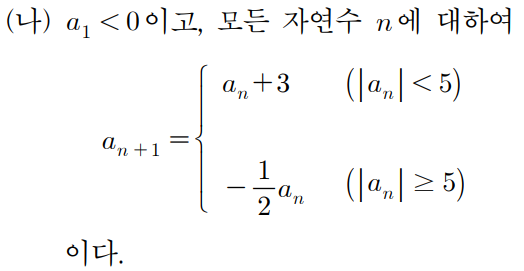
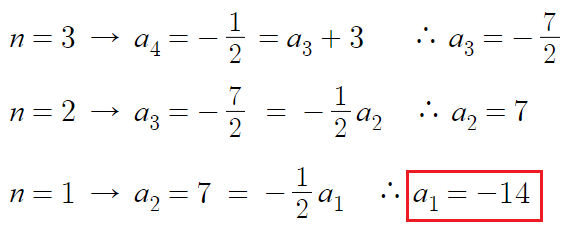
따라서, a₁ = -14 이다.
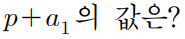
이제 p값만 알아내면 된다.
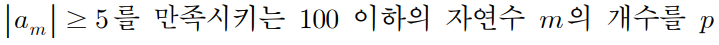
수열의 항 값의 크기가 5 이상이 몇 번 되는가? 를 묻는다.

이 그래프를 잘 관찰하면, 주기성을 찾을 수 있다.
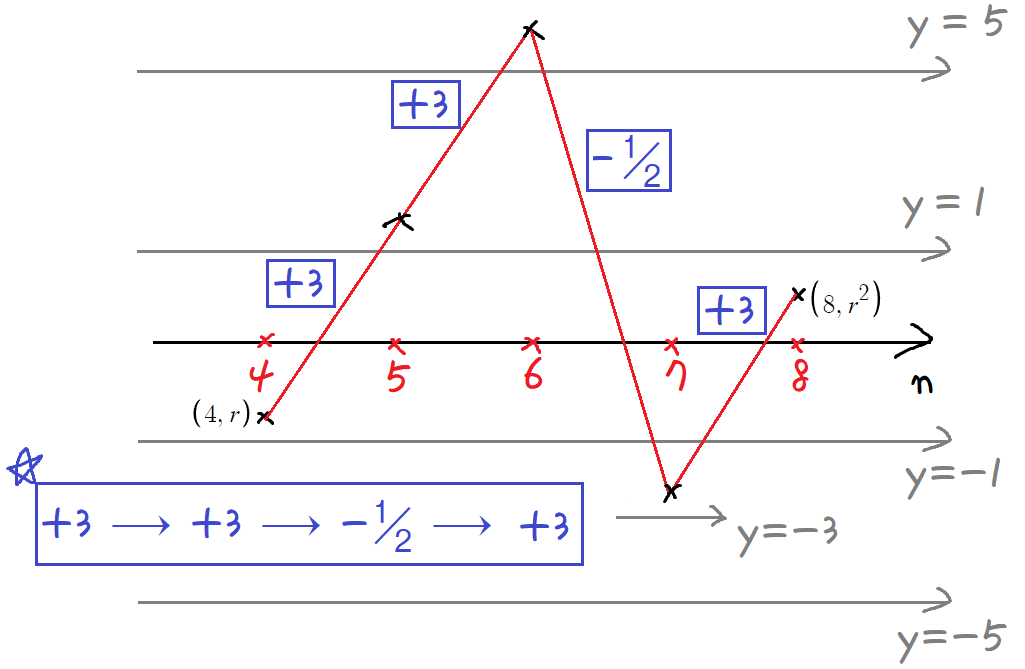
어차피 구간 [4k, 4k+4] 에서는
+3 → +3 → -½ → +3 이라는
똑같은 경향성을 가지고 값이 변할수밖에 없다.
r은 몇제곱해도 무조건 1과 -1 사이일것이기 때문이다.
따라서, 구간 [4k, 4k+4] 에서
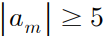
위 식을 만족하는 m값은 '한 번' 나온다.
그리고 그런 '구간'은
n=4k인데 n은 1부터 100 까지의 값이니
자연수 k는 딱 24개 존재한다.
즉, +3 → +3 → -½ → +3
이라는 경향성을 가지고 값이 변하는 '구간'은 총 24번 나오며,
'구간'이 한 번 나올때마다, 'm값'도 한 개씩 나온다.
따라서, n=4부터 n=100까지 m값은 총 24개 존재한다.
이제 n=1부터 n=3 까지의 m값 개수만 더해주면 된다.
a₁ = -14 < -5 이므로, 이때 m값 하나 존재
a₂ = 7 > 5 이므로, 이때도 m값 하나 존재
a₃ = -7/2 > -5 이므로, 이때는 m값 존재하지 않음
따라서, n=1부터 n=3 까지 m값은 총 2개 존재한다.
따라서, p = 24+2 = 26
- 마무리계산 -
a₁ = -14 이므로
p + a₁ = 26-14 = 12
따라서 답은 3번
'2023학년도 기출 해설 > 2023학년도 9월 모의평가 해설' 카테고리의 다른 글
| 2023학년도 9월 모의평가 물리II 해설 (2) | 2022.09.25 |
|---|---|
| 2023학년도 9월 모의평가 물리I 해설 (1) | 2022.09.21 |
| 2023학년도 9월 모의평가 수학 확률과통계 23번~30번 해설 (0) | 2022.09.19 |
| 2023학년도 9월 모의평가 수학 미적분 23번~30번 해설 (0) | 2022.09.08 |
| 2023학년도 9월 모의평가 수학 공통 16번~22번 해설 (0) | 2022.09.05 |



