
- 개요 -
그냥 지수와 로그의 확장 개념이고
전혀 쫄게 없다.
거듭제곱에서 지수를 x에 대해 나타낸 함수가 지수함수고
로그에서 진수를 x에 대해 나타낸 함수가 로그함수다.
이 정도만 할 수 있으면 된다.
1. 지수함수와 로그함수의 그래프 그리기
2. 지수함수와 로그함수의 최대, 최소
3. 지수함수와 로그함수의 역함수관계 이해
4. 지수함수와 로그함수의 방정식, 부등식 풀이
- 지수함수의 그래프 -

이게 지수함수다.
a가 밑이고 x가 지수이다.
여기서 '밑'이 얼마냐에 따라 그래프의 개형이 달라진다.
우선 저 값이 정의되기 위해서는
밑이 양수여야 하고
만약 밑이 1 즉 a=1 이면
x가 몇이든 무조건 y=1 이고

그러면 이렇게 y=1 인 상수함수가 되어버리기 때문에
지수함수라 하지 않는다.
따라서 지수함수가 정의되기 위한 밑의 조건은
1. 양수여야 함
2. 1이면 안됨
이제 그래프를 그려볼건데
0<a<1 인 경우와
1<a 인 경우의 그래프의 모양이 다르기때문에
이 둘을 나눠서 다룰것이다.
1. a>1 인 경우
1보다 큰 수는
많이 제곱할수록 거듭제곱의 값은 점점 커진다.
즉 지수가 커질수록 a^x 값이 커진다는거고
따라서 이때 지수함수는 x가 증가하면 y도 증가하는 증가함수이다.
그리고 x가 커지면 그에 따라 y값도 기하급수적으로 커지므로
이 함수의 그래프는 막힘없이 쭉 올라가는 모양일것이다.
근데 x가 엄청나게 작은 수라고 해보자.
이때 a^x 값도 막힘없이 쭉 내려갈까?
a^x에서 x가 음수면
1/a^몇제곱 꼴로 나타내어질텐데
분수가 0이 되려면 분자가 0이 되는 수 밖에 없다.
근데 분자는 상수 1로 고정되어있으므로
절대 0이 될 수 없다.
대신 0에 가까워지긴 한다.
x가 엄청나게 작다고 하면
1/a^몇제곱 여기서 분모가 엄청나게 커져서
거의 0에 가까워질것이다.
따라서 y=0을 점근선으로 하는 이러한 그래프가 그려질것이다.

2. 0<a<1 인 경우
1보다 작은 수는
거듭제곱할수록 작아진다.
따라서 이 함수는
x가 증가하면 y는 감소하는 감소함수이다.
이것도 아무리 x가 커져봐야
거듭제곱의 값은 무조건 양수기때문에
y값은 절대 0이될순 없고
다만 아까와 같은 논리로 0에 아주 가까워지긴 할테니
y=0을 점근선으로 하는 이러한 그래프가 그려질것이다.

- 로그함수의 그래프 -
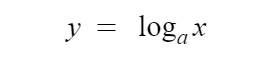
이게 로그함수다.
a가 밑이고 x가 진수이다.
여기서도 '밑'이 얼마냐에 따라 그래프의 개형이 달라진다.
우선 저 값이 정의되기 위해서는
밑이 양수여야 하고
밑이 1이면 안된다.
그리고 여기서도
밑이 1보다 크냐 작냐에따라 그래프의 개형이 달라진다.
1. a>1 인 경우
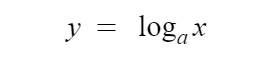
이것의 의미는
a를 y제곱하면 x가 된다는 것이다.
따라서 x가 커지면
더 많이 거듭제곱해줘야 하기 때문에
y도 따라서 커진다.
따라서 이건 증가함수이다.
근데 로그의 정의 상
진수는 무조건 양수여야한다.
따라서 x>0 에서만 정의되는 함수이다.
그럼 x가 0에 아주 가깝다면 어떻게 될까?
a는 밑인데 1보다 크니까
얘를 아주 작은 수로 거듭제곱해주면
0에 가깝게 작아질것이다.
예를들어 a=2라고하면 2의 -9999제곱정도 해주면
거의 0에 근접한 수가 나온다는것이다.
그리고 여기서의 -9999가 바로 y값이다.
즉 x가 0에 가까워질수록 기하급수적으로 y값이 감소한다.
따라서 이건
x=0을 점근선으로 하는 함수이다.
개형은 이렇게 생겼다.
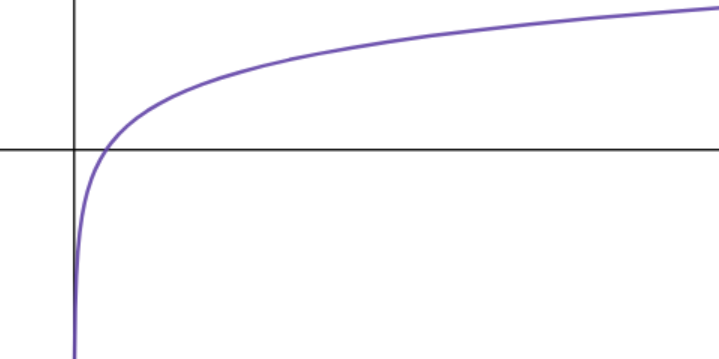
2. 0<a<1 인경우
이때도 a를 y제곱하면 x가 되는데
a가 1보다 작기때문에
많이 거듭제곱할수록 x값은 작아지게 될것이다.
즉 x값이 작아지면 y값은 커진다.
따라서 이건 감소함수이다.
그리고 이것도
로그의 진수 조건에 의해 x>0 이어야 하고
x가 0에 아주 가까이 갔다고 하면
1보다 작은수를 y제곱한게 0에 매우 가까워야하므로
y는 매우 커야한다.
1보다 작은수는 거듭제곱할수록 작아지기 때문이다.
즉 0에 가까워질수록 기하급수적으로 커진다.
따라서 이것도 x=0을 점근선으로 하는 함수이다.
개형은 이렇게 생겼다.
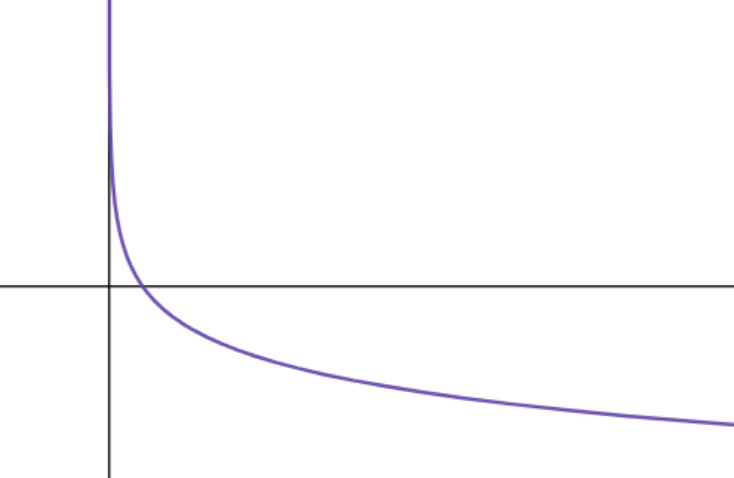
- 평행이동과 대칭이동 -
예를 들어
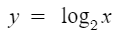
이걸 x방향으로 3만큼, y방향으로 2만큼 평행이동 했다고 해보자.
그러면 x자리에 x-3 넣고 y자리에 y-2 넣어서 이렇게 될것이다.
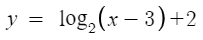
여기서 핵심은
1. 점근선의 위치가 바뀐다.
2. 그래프의 모양은 변하지 않는다.
점근선의 위치가 바뀌는 이유는
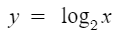
얘의 점근선이 x=0 이었던 이유는
로그의 진수 조건에 의해 x>0 에서만 정의되기 때문이었다.
그럼
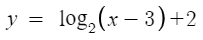
얘는 로그의 진수 조건에 의해
x-3>0 이어야 하고 따라서 점근선의 위치가 x=3 이 된다.
직관적으로 설명하자면
x방향으로 3만큼 평행이동한거니 점근선도 당연히 3만큼 따라온다.
그리고 그래프의 모양은 당연히 변하지 않는데
평행이동이란건 그냥 x방향 y방향으로 그래프를 움직였다는거라서
그래프의 모양 자체에는 어떠한 영향도 주지 못한다.
지수함수도 똑같으니 똑같은말은 반복하지 않겠다.
직접 해보기 바란다.
이번엔 이걸 대칭이동해보자.
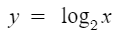
x축으로 대칭이동하면
x축을 기준으로 위아래를 바꾼다는 것이므로
y가 -y로 바뀐다.
따라서 아래와 같이 될것이다.
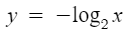
여기서도 그냥 뒤집은것 뿐이지
그래프의 모양 자체는 변하지 않으므로
어렵게 생각할 필요가 없다.
그냥 위아래가 바뀐거다.
이번엔 y축으로 대칭이동하면
y축을 기준으로 좌우를 바꾼다는 것이므로
x가 -x로 바뀐다.
따라서 아래와 같이 될것이다.
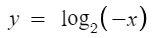
이것도 그냥 뒤집은것 뿐이다.
다만 조금 생각할건
로그의 진수 조건에 의해
-x>0 이어야 하므로
이 함수의 정의역은 x<0 이라는것이다.
직관적으로 설명하자면
x>0에서 정의되는걸 y축 기준으로 뒤집었으니
당연히 x<0에서 정의되는 함수로 바뀐다.
결론내자면
문제에서 제시된 지수 로그함수들이
대칭이동되고 평행이동되어있다고 겁먹을게 없다.
그냥 식좀 복잡하게 만들고
생각좀 더하게 만들려는거다.
- 지수함수의 최대, 최소 -
우선 지수함수는 알다시피
a>1이면 계속 증가하기만하는 증가함수이고
a<1이면 계속 감소하기만하는 감소함수이다.
증가함수, 감소함수임을 이용해 최대, 최소를 구하면 된다.
근데 전체 x 범위에서 따지면
당연히 최댓값, 최솟값은 존재하지 않는다.
무한이 최댓값 아니냐 할 수 있는데
무한이라는건 엄청나게 크다는 표현일 뿐이지
실재하는 수가 아니다.
그래서 문제에서는 보통 [2,5] 범위에서 구하라던지 해서
범위를 정해준다.
4가지 정도의 유형이 있다.
1. 지수가 1차식
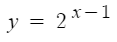
그냥 y=2^x 를 x방향으로 1만큼 평행이동한것 뿐이다.
따라서 그래프의 개형을 그릴 수 있는 경우이며
평행이동은 그래프의 모양 자체에는 어떠한 영향도 주지 못한다.
따라서 이게 증가함수라는건 변함이 없고
그걸 이용해서 구하면 된다.
예를들어 [2,5] 범위에서 구하라 하면
증가함수니까 당연히 x가 클수록 함숫값은 커진다.
x=2에서 최솟값, x=5에서 최댓값을 가질것이다.
2. 지수가 2차원 이상인 식
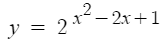
이 경우는
평행이동도 아니고 대칭이동도 아니라서
그래프의 개형을 그려볼수가 없다.
이럴땐 지수함수의 특징을 이용하는것이다.
밑이 2 이므로 밑이 1보다 큰 지수함수이다.
따라서 지수가 커질수록 함숫값도 커진다.
즉 여기서의 최댓값을 구하라 하면
지수가 최대가 될때의 값을 구하면 되는것이고
최솟값을 구하라 하면
지수가 최소가 될때의 값을 구하면 되는것이다.
예를들어 [0,3] 범위에서 구하라 하면
지수가 최소가 될때는 x=1 일때 이므로
x=1에서 최솟값을 갖고,
x²-2x+1은 [0,3] 범위 내에서
x=3 일때 최대이므로
x=3에서 최댓값을 가질것이다.
3. 치환해야 하는 경우
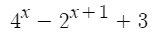
이 경우에도 개형을 그릴수 없다.
하지만 4가 2의 제곱이므로
이럴때는 치환해서 풀면 된다.

이렇게 치환하고 나면 이젠
X에 대한 이차식의 최대, 최소를 구하는 문제로 바뀐다.
단 주의할 점은
2^x = X 로 치환했는데
2^x 는 무조건 양수이기 때문에
X>0 이라는 범위가 생긴다.
만약 (2,3) 범위 내에서 최대 최소를 구하라 하면
2^2은 4 이고
2^3은 8 이므로
4<X<8 이라는 범위가 생긴다.
4. 지수가 로그 형태로 나타내어진 경우
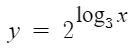
양변에 로그를 취하면 된다.
저기서는 밑이 2니까
양변에 log_2를 취하면
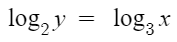
이런식으로 바뀌게 되고
이제 y의 최대, 최소를 구하기 위해
log₂y의 최대, 최소를 구한 다음
그에 따른 y값만 빼내면 된다.
만약 [3,9] 범위 내에서 최대 최소를 구하라 하면
log₃X는 증가함수이므로 x=3에서 최소, x=9에서 최대이고
x=3에서 log₂y의 값은 1이므로 최솟값은 y=2
x=9에서 log₂y의 값은 2이므로 최솟값은 y=4
- 로그함수의 최대, 최소 -
이것도 사실 지수함수 푸는것과 똑같다.
1. 진수가 1차식인 경우
2. 진수가 2차원 이상의 식인 경우
3. 치환해야 하는 경우
1. 진수가 1차식인 경우
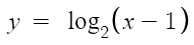
일단 밑이 1보다 크므로 증가함수이고
그냥 x방향으로 1만큼 평행이동 한것이다.
지수함수 풀때와 같은 논리로 풀면 된다.
2. 진수가 2차원 이상의 식인 경우
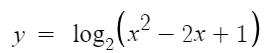
밑이 1보다 크므로 증가함수이다.
따라서 진수가 최대가 될때 최댓값을 갖고
진수가 최소가 될때 최솟값을 갖는다.
지수함수 풀때와 똑같은 말을 반복하고있기 때문에
이정도만 설명하고 넘어간다. 수학공부는 스스로 하는거다.
3. 치환해야 하는 경우
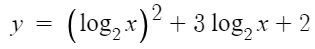
로그를 제곱한다음 거기다 로그를 더한것의 개형을 그리라는데
당연히 못그린다.
이때도 치환해서 풀면 된다.
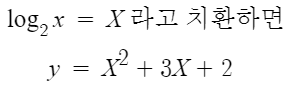
이러면 이차식이 되고 아까 지수함수문제 풀듯이 풀면 된다.
단 여기서는
log₂x 의 범위가 (-∞,∞) 이므로
X의 범위가 발생하지 않는다.
간단한 문제로 중간점검

지수함수 f(x)의 밑이 1보다 작으므로 감소함수이다.
따라서 닫힌 구간 [-2, 1] 에서
x=1에서 최솟값 5/6
x=-2에서 최댓값 M을 갖는다.
따라서 f(1)=5/6 임을 이용해 a를 구하고
f(-2)=M 임을 이용해 M을 구하면 된다.
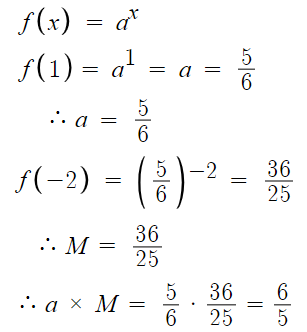
따라서 답은 5번
너무 쉬운데 이게 수능 이과수학 3점짜리다.
- 지수함수와 로그함수의 관계 -

이런 두 함수가 있다고 해보자.
이제 이 둘을 합성해볼것이다.
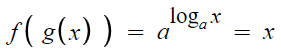
역함수를 배웠으면 알겠지만
어떤 함수와 그것의 역함수를 합성하면 항등함수가 된다.
근데 f(x)와 g(x)를 합성했더니 항등함수가 되었다는건
g(x)가 f(x)의 역함수라는거다.
따라서 다음과 같이 결론내릴 수 있다.
로그함수는 지수함수의 역함수이다.
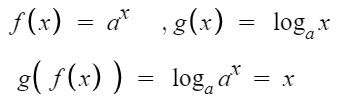
이번엔 g(x)에 f(x)를 합성해보았다.
역시 항등함수가 나오는것을 알 수 있다.
따라서 다음과 같이 결론내릴 수 있다.
지수함수와 로그함수는 서로 역함수 관계이다.
그리고 역함수라는건 y=x 에 대해 대칭이라는거다.
이는 문제로 자주 출제되는 재료이므로 꼭 알아둬야한다.
- 지수 로그함수 방정식의 풀이 -
이는 사실 설명해주지 않아도 알아서 할 수 있다.
지수법칙과 로그의 성질을 이용하는거기 때문이다.
못믿겠으면 아래 문제를 풀어봐라.

무려 4점짜리문제인데
앞의 내용들을 잘 이해하고 있다면
무리없이 쉽게 풀 수 있다.

따라서 답은 4
그냥 지수법칙과 로그의 성질 가지고 문제푸는거랑 똑같다.
내 글의 첫 문단이 틀린 말이 아님이 증명되는 순간이다.
- 지수 로그함수 부등식의 풀이 -
이것도 사실 설명해주지 않아도 된다.
지수법칙과 로그의 성질을 이용하는거기 때문이다.
밑을 같게 한다음 하던대로 하면 된다.
단 주의할게 있다면
밑이 1보다 크냐 작냐를 따져봐야한다.
그리고 만약 로그함수 부등식의 풀이라면
진수조건을 만족하는지도 체크해야한다.
밑이 1보다 큰지 작은지를 따지는 이유는
아래 문제를 풀어보면 알 수 있다.

이걸 풀어보자.
일단 밑이 1보다 크기 때문에 둘다 증가함수이다.
그리고 둘다 밑이 2로 같다.
따라서 지수가 큰 쪽이 거듭제곱한 값이 더 크다.
따라서 x+3 > -x-7 을 만족하는 x의 범위를 구하면 되는거다.
구하면 x>-5 라는게 나올거다.
그럼 이번엔 이걸 풀어보자.

일단 밑이 1보다 작기 때문에 둘다 감소함수이다.
그리고 둘다 밑이 1/2 로 같다.
따라서 지수가 작은 쪽이 거듭제곱한 값이 더 크다.
따라서 x+3 < -x-7 을 만족하는 x의 범위를 구하면 되는거다.
구하면 x<-5 라는게 나올거다.
왜 정반대의 결과가 나온걸까?
밑이 1보다 작으면 감소함수고
밑이 1보다 크면 증가함수이기 때문이다.
따라서 밑이 1보다 크면
지수가 큰쪽이 거듭제곱한 값이 크니까
지수의 대소가 곧 거듭제곱한 값의 대소가 되기 때문에
이때 지수를 비교할때는 부등호 방향이 그대로다.
근데 밑이 1보다 작으면
지수가 작은쪽이 거듭제곱한 값이 크니까
지수의 대소의 반대가 곧 거듭제곱한 값의 대소가 되기 때문에
이때 지수를 비교할때는 부등호 방향을 반대로 해야한다.
헷갈리면 이렇게 해보자.
1/2 의 x+3 제곱은
2의 -(x+3) 제곱과 같으니까
이런식으로 바꿔서 구해도 된다.
결론은
밑이 1보다 크면 부등호 그대로
밑이 1보다 작으면 부등호 반대
물론 로그함수도 이와 같음
이거 외에는 그냥 똑같다.
아래 문제를 풀어보자.
- 예제 -

첫번째 풀이

두번째 풀이

따라서 답은 x≥2
'수학I > I. 지수함수와 로그함수' 카테고리의 다른 글
| 로그의 정의와 성질 (0) | 2021.09.11 |
|---|---|
| 지수법칙 - 중등수학 지수법칙의 확장 (0) | 2021.09.09 |

