
- 개요 -
수열은
최근 수능수학 킬러 포지션에 있는 단원이다. 15번으로 자주 나온다.
어려워서 틀린다기보단
수학I 이다보니까
다른 과목 하느라 공부를 안해서 틀린다고 보는게 맞다.
이번엔 수열의 기본 정의와 용어만 알아볼것이다.
- 수열의 정의 -
영어로는 sequence 이다.
즉 수열이란 수를 순서 있게 나열한 것이다.
1, 2, 3, 4, 5 같은 게 수열이다.
수를 순서 있게 나열하기만 하면 되기 때문에
수열엔 규칙이 없어도 된다.
9, -π, 0.39, sin11°, 0 이런것도 수열이다.
다만 순서 있게 나열해야 하기 때문에
1, 2, 3, 4, 5와
2, 1, 3, 4, 5는 다른 수열이다.
여기서 수열을 이루는 각각의 수를 '항(term)' 또는 '원소(element)'라고 한다.
가령 수열 1, 3, 5, 7, 9 가 있다고 하면
1도 이 수열의 항이고
5도 이 수열의 항이다.
1은 이 수열의 첫 번째 항이므로
첫째항 또는 제1항 으로 부른다.
3은 두 번째 항이니까
둘째항 또는 제2항 이라 부른다.
- 수열의 일반항 -
수열을 나타낼 때는
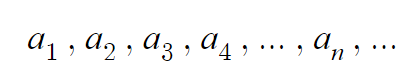
이와 같이 나타낸다.
첫번째 항은 a₁
두번째 항은 a₂
이런식으로 나타낸것이다.
여기서 n번째 항인

이걸 수열의 일반항 이라고 한다.
즉 어떤 수열의 n번째 항이 수열의 일반항이다.
일반항이 a_n 인 수열을 간단하게 아래와 같이 나타낸다.

아까 예로 들었던 수열 { 1, 3, 5, 7, 9 }의 일반항을 구해보자.
n번째 항의 값을 구하면 그게 일반항이다.
따라서 일반항은 2n-1 이다.
n=1이면 a₁ = 1
n=2이면 a₂ = 3
n=3이면 a₃ = 5
- 심화 : 수열은 함수이다 -
아까 예로 들었던 수열을 또 가져와보겠다.
{ 1, 3, 5, 7, 9 }
이 수열의 일반항은
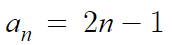
이다.
여기서 핵심은
이 수열의 어떤 항의 값은
몇 번째 항인지에 따라 정해진다는것이다.
즉 n이 몇이냐에 따라 정해지는 값이다.
예를 들어 3번째 항은 n=3일때 2×3 - 1 = 5 이므로
이 수열의 3번째 항은 5 라는걸 알 수 있다.
이런 수열도 있을 수 있다.
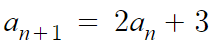
이것도
a_n 이 몇이냐에 따라 정해지는 값이다.
그리고 a_n도 n이 몇이냐에 따라 정해지는 값이기 때문에
결국 a_n+1 도 n이 몇이냐에 따라 정해지는 값이다.
함수 f(x)의 값이 x가 몇이냐에 따라 정해지는것처럼
수열의 n번째 항의 값도 n에 따라 정해진다는 것이다.
따라서 다음과 같은 결론에 도달한다.
수열의 일반항은 정의역이 자연수인 함수라고 볼 수 있다.
정의역이 자연수인 이유는 지극히 당연한건데
1.5번째항 이나 -2번째항 같은건 없기때문이다.
- 예제 -

ㄱ )
수 6개를 순서 있게 나열한 것이므로
항이 6개인 수열이다.
따라서 ㄱ(o)
ㄴ )
수열엔 규칙이 없어도 된다.
즉 A=10이라고 장담할 수 없다.
A=π 여도 수열이고 A=-2 여도 수열이다.
따라서 ㄴ(x)
ㄷ )
저건 수열이고
3번째 항은 6이다. 따라서 ㄷ(o)
ㄹ )
수열의 일반항 = 수열의 n번째 항
따라서 A=10 이면 이 수열의 일반항은 2n 이다.
일반항이 2n+2라면
{ 4, 6, 8, 10, 12, 14 } 가 됐을거고
문제의 조건을 만족시키지 못한다.
따라서 ㄹ(x)
ㅁ )
A=10이면 이 수열의 일반항은 2n이고
수열의 일반항은 정의역이 자연수인 함수라고 볼 수 있다.
이 수열은 항이 6개니까
정의역이 { n|n=1,2,3,4,5,6 } 인 함수 f(n)과 동치이다.
따라서 ㅁ(o)
따라서 답은 ㄱ,ㄷ,ㅁ



