
홀수형 기준입니다.
혹시 본인이 못 푼 문제인데
어떻게 푸는건지 궁금해서 이 글을 보는거라면
이 글을 보지 말것.
남이 풀어주는걸로는 실력이 늘지 않는다.
풀긴 풀었는데 풀면서 100%확신하진 못하고 약간 찜찜했거나
다른 풀이도 있을까 해서 찾아보는거라면
매우 환영이다.
원하시는 문제로 바로 가고싶으면
N번 문제로 가고싶다면
N )
이 형태로 검색하시면 됩니다.
예를들어 2번으로 가고싶으면 2 )
쉬운건 빠르게 넘어가면서
비약 하나도 없이 풀어보겠습니다.
1 )

말 많은 1번 문제
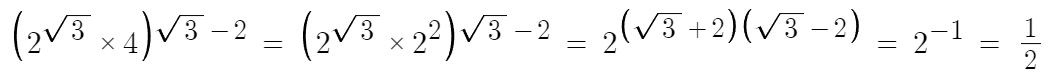
따라서 답은 2번
2 )

f'(x) = 3x²+6x+1 이고
따라서 f'(1) = 10 답은 5번
3 )

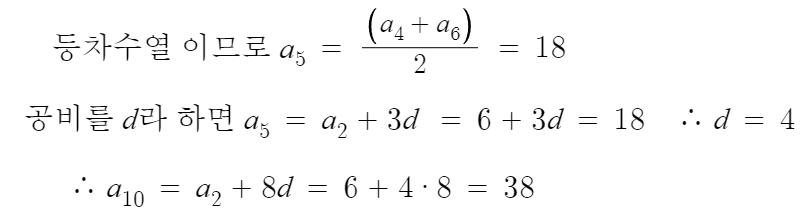
따라서 답은 5번
4 )

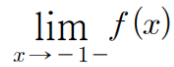
이것의 의미는 함수 f(x)의 x=-1에서의 좌극한값이고 3이다.
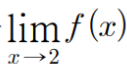
이것의 의미는 함수 f(x)의 x=2에서의 극한값이고 1이다.
3+1 = 4
따라서 답은 4번
5 )

8항까지만 더하는거니 직접 하나씩 대입할것이다.
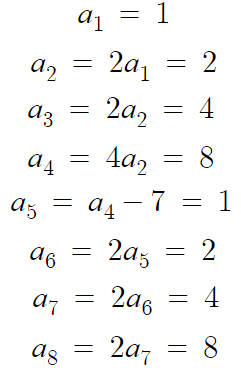
1항부터 8항까지 모두 더하면
1+2+4+8+1+2+4+8 = 30
따라서 답은 1번
6 )

k를 우변으로 이항하면
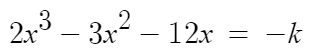
이렇게 되고 이것이 서로 다른 세 실근을 갖도록 하면 된다.
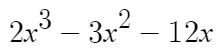
이것의 그래프를 그리기 위해 일단 이걸 미분하면
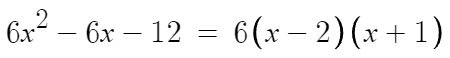
따라서 x=-1 에서 극대, x=2 에서 극소이다.
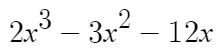
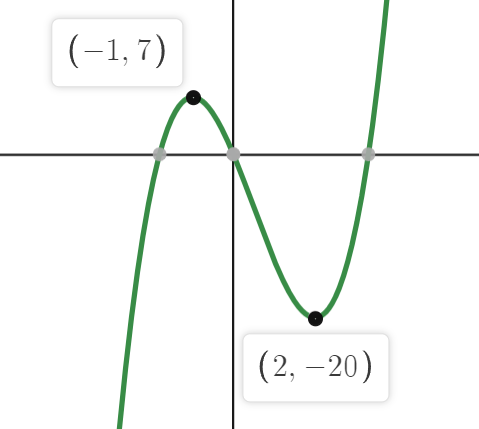
극대점은 x=-1 대입하면 ( -1, 7 ) 이며
극소점은 x=2 대입하면 ( 2, -20 ) 이다.
이를 토대로 그래프를 그리면 아래와 같다.
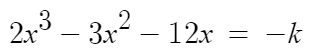
따라서 이 식이 서로다른 세 실근을 가지려면
y=-k 가 극댓값과 극솟값 사이에 있어야한다.
즉 -k가 7보단 작고 -20보단 커야한다.
-20<-k<7
따라서 -7<k<20 이고
이를 만족하는 정수 k는 -6, -5, -4, ... , 18, 19 이며 26개이다.
따라서 답은 3번
7 )


따라서 답은 1번
8 )



따라서 답은 1번
9 )

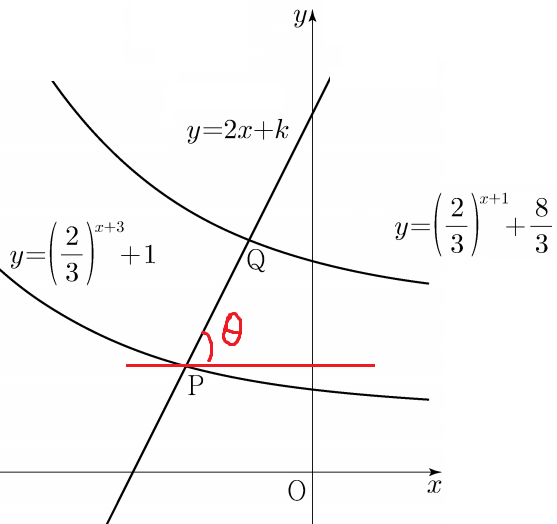
y=2x+k 가 x축의 양의 방향과 이루는 각을 θ 라 하면
tanθ = 2 이다.
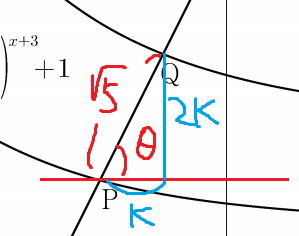
즉 P점과 Q점의 x값 차이를 k라 하면
P점과 Q점의 y값 차이는 2k이고
피타고라스 정리를 이용하면
k² + 4k² = 5 이므로 k = 1 이다.
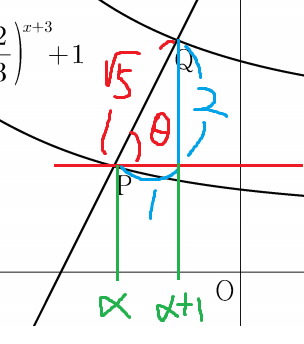
이때 P점의 x좌표를 α 라 하면
Q점의 x좌표는 α+1 이 된다.

따라서 답은 4번
10 )


이 문장에 의해 f(0) = 0 이고

이 문장에 의해 f(1) = 2 이다.
y=f(x) 위의 점 (0, 0) 에서의 접선과
y=xf(x) 위의 점 (1, 2) 에서의 접선이 일치한다는건
기울기가 같다는거다.
따라서 y=f(x)를 미분한다음 0을 대입한것과
y=xf(x)를 미분한다음 1을 대입한것의 값이 같다.
f'(0) = f(1) + f'(1) = 2+f'(1)
y=f(x) 위의 점 (0, 0) 에서의 접선을 l₁(x) 라 하고
y=xf(x) 위의 점 (1, 2) 에서의 접선을 l₂(x) 라 하면
l₁(x) = f'(0)(x-0) + 0 = f'(0)x
l₂(x) = ( f(1)+f'(1) )(x-1) + 2 = ( 2+f'(1) )x - f'(1)
f'(0)x = ( 2+f'(1) )x - f'(1) 이므로 f'(1) = 0 이고
f'(0) = 2 이다.
f(x)는 삼차함수이므로
f(x) = ax³ + bx² + cx + d 라 하면
f'(x) = 3ax² + 2bx + c 이다.
f(0)=0 , f(1)=2 , f'(1)=0 , f'(0)=2 임을 이용해
각각 대입해보면
f(0) = d = 0
f(1) = a+b+c = 2
f'(1) = 3a+2b+c = 0
f'(0) = c = 2
a+b+c=2 와 3a+2b+c=0을 뺄셈 연립하면
2a+b=-2
a+b+c=2 인데 c=2 이므로 a=-b
따라서 -2b+b = -b = -2
따라서 b=2, a=-2 이고
f(x)는 -2x³ + 2x² + 2x 가 된다.
따라서 f'(x) = -6x² + 4x + 2 이고
f'(2) = -24 + 8 + 2 = -14 이다.
따라서 답은 5번
11 )

우선 A지점과 C지점은
x축과 평행한 직선이 f(x)와 만나는 지점이기 때문에
A지점과 C지점의 y좌표는 같다.
tanx의 그래프를 보자.

tanx는 주기가 π인 주기함수이다.
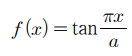
따라서 f(x)의 주기는
πx/a = π 가 되도록 하는 x값이고
그것은 a이다.
따라서 f(x)의 주기는 a이다.
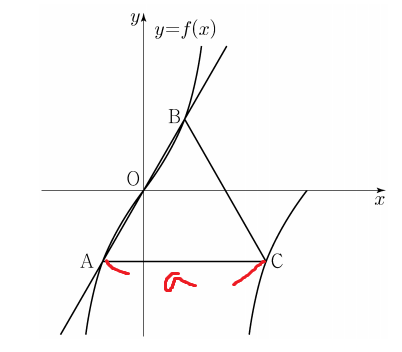
따라서 AC의 길이가 a이다.
ABC는 한 변의 길이가 a인 정삼각형인것이다.
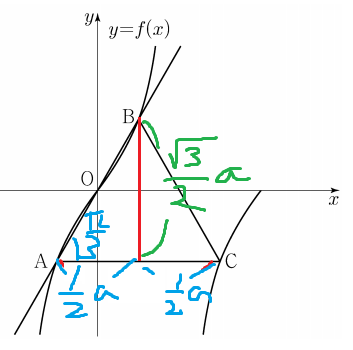
ABC는 정삼각형이기 때문에
점 B에서 AC에 수선의 발을 내리면
선분 AC를 이등분 하고
이때 수선의 길이는 a/2 × sin(π/3) 이다.
그리고 tan(πx/a) 는 원점 대칭이고
A와 B를 지나는 직선이 원점을 지나므로
점 A와 점 B는 원점대칭이다.
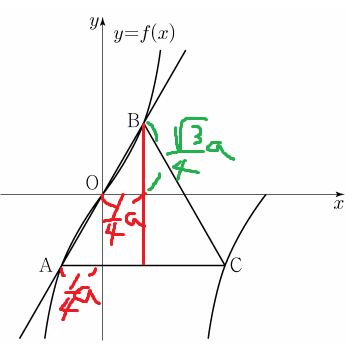
따라서 B점의 y좌표는 sqrt(3)a/4 이고
x좌표는 a/2를 반으로 나눈 a/4 이다.
이제 f(x)에 대입하면
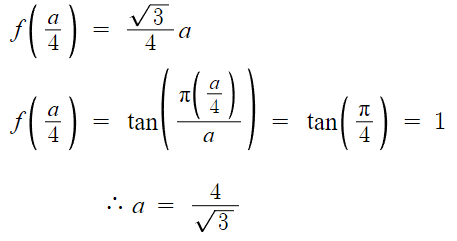
a가 정삼각형 ABC의 한 변의 길이이니
넓이를 a에 대해 나타낸 다음 a값을 대입하면 끝난다.
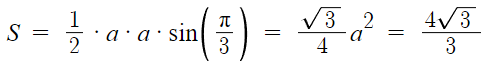
따라서 답은 3번
12 )

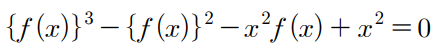
이 식에 대입해서 하나씩 구해볼건데
f(0)부터 구해볼것이다.
x=0을 대입한다.
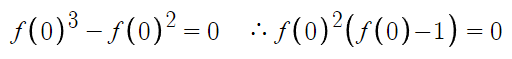
따라서 f(0)=0 이거나 f(0)=1 이다.
근데 f(x)의 최솟값이 0이라고 한다.
이번엔 반대로
f(x)의 최솟값이 0이므로
f(x)=0 이 되도록 하는 x가 어딘가엔 존재할거고
그 x값을 k라 한 뒤
f(k)=0 , x=k 를 대입해서 정리하면
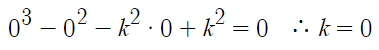
이 식을 만족하는 k값은 0 하나밖에 없고
따라서 f(0) = 0 이다.
이번엔 f(-4/3) 을 구해보자.
아까처럼 x=-4/3 을 대입한다.

이제 f(1/2) 만 구하면 된다.
x=1/2 를 대입한다.

이제 f(1/2) = 1 과 f(1/2) = 1/2 중 말이 안되는 것을 걸러내면 된다.
아직 문제에서 쓰지 않은 조건이 있다.
f(x)가 연속이라는 것이다.
f(x)가 연속이기때문에
f(x)의 최솟값이 0이고 최댓값이 1이면
f(x)가 연속이어야 하므로 f(x)=0 과 f(x)=1 사이의 값인
f(x)=1/2 를 만족하는 x는
무조건 존재해야한다.
따라서 아까 최솟값 구할때 f(k)=0, x=k 라 뒀던것처럼
이번엔 f(a)=1/2 , x=a 라 둘것이다.
이걸 만족하는 a값은 무조건 존재해야한다.
f(x)가 연속이기 때문이다.
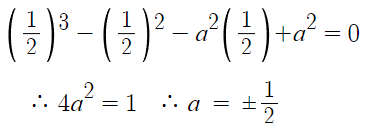
따라서 f(x)는 x=-1/2 , x=1/2 에서
f(x)=1/2 를 만족해야만 한다.
따라서 f(1/2) = 1/2 이다.
따라서 f(-4/3) + f(0) + f(1/2) = 1 + 0 + 1/2 = 3/2
따라서 답은 3번
13 )

나라면 log₂(x) 와 log₄(x)의 그래프부터 그려보고 싶다.
log₂(x) 의 ( a, log₂a ) 와 ( b, log₂b ) 를 지나는 직선의 y절편과
log₂(x) 의 ( a, log₄a ) 와 ( b, log₄b ) 를 지나는 직선의 y절편이
같다는 말이다.
log₄(x) = 1/2 × log₂(x) 이다.
즉 log₂(x) 의 ( a, log₂a ) 와 ( b, log₂b ) 를 지나는 직선의 기울기를 m이라 하면
log₂(x) 의 ( a, log₄a ) 와 ( b, log₄b ) 를 지나는 직선의 기울기는 m/2 이다.
log₂(x) 의 ( a, log₂a ) 와 ( b, log₂b ) 를 지나는 직선의 방정식을 l₁(x)
log₂(x) 의 ( a, log₄a ) 와 ( b, log₄b ) 를 지나는 직선의 방정식을 l₂(x)
라고 하고 각각 식을 써보면
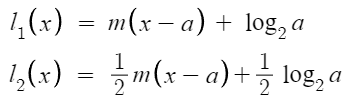
이 둘의 y절편이 같으므로
두 직선의 방정식에 x=0을 대입했을때의 함숫값이 같다고 하면 된다.

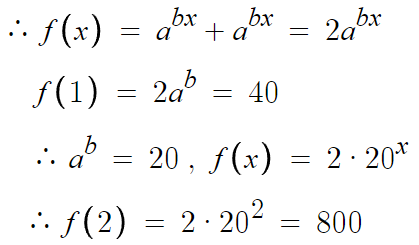
따라서 답은 2번
14 )

연필도 안대고 풀수 있는문제이다.
ㄱ )
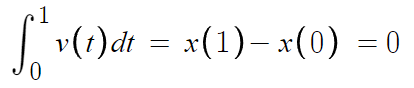
따라서 ㄱ(o)
ㄴ )

이 명제가 참임을 ㄱ 선지를 풀면서 알았다.
저것의 의미는
점 P의 위치 변화량이 0이었다는거다.
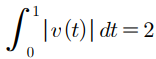
이건 문제에서 제시된 조건인데
이것의 의미는
점 P의 '이동거리'가 2였다는거다.
위치 변화량은 0인데 이동거리는 2라는거는
일단 점 P가 가만히 있지는 않았고
뭔가 2만큼 움직이기는 했는데
최종 위치는 제자리로 돌아온 것임을 알 수 있다.

ㄴ 선지에서는 지금 이게 참이냐고 묻고있다.
우선 x(0) = 0(원점) 이므로
점 P가 원점에서 1보다 멀리 떨어지는 순간이
0<t<1 에서 존재하냐는 것이다.
근데 상식적으로 생각해보자.

이것에 의해 위치의 최종 변화량은 0이다.
즉 제자리로 돌아와야한다.
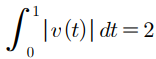
이것에 의해 이동거리는 2이다.
이때 점 P가 원점에서 가장 멀리 떨어질 수 있는 경우는 어떤 때인가?
딱 x(t) = 1 까지만 갔다가 그대로 돌아오는 경우이다.
왜냐면 | x(t)>1 | 인 순간이 존재한다면
이 순간까지의 이동거리는 1보다 큰데
어차피 결국 원점으로 돌아가야한다.
원점으로 돌아갈때의 이동거리도 1보다 크게 되므로
이때의 최종 이동거리는 2보다 커져버리게 되고
결국 이동거리가 2라는 문제의 조건을 만족하지 못하게 된다.
따라서 | x(t₁)>1 | 을 만족하는 t₁은 열린 구간 (0, 1)에서 존재할 수 없다.
따라서 ㄴ(x)
ㄷ )
0≤t≤1 인 t에서 | x(t) | < 1 이라는건
-1 < x(t) < 1 이라는건데
이건 무슨말이냐면 점 P가 -1<x<1 안에서만 움직였다는말이다.
문제에서 제시한 x(t)는 삼차함수이다.
즉 v(t)는 이차함수이고
v(t)=0 을 만족시키는 t값은 최대 2개이다.
v(t)=0 을 만족시킨다는건 방향전환이 일어난다는거다.
그리고 x(t) 의 근은 t=0, t=1, t=b/a 이다.
b/a = 0 이나 b/a = 1 을 만족한다고 해도
x(t)의 근은 무조건 두개 이상이다.
따라서 v(t)=0 의 근은 무조건 하나 이상 존재하며
이차함수니까 최대 2개 존재한다.
즉 방향전환이 한번 일어나거나 두번 일어난다.
방향전환이 한번 일어나는경우는 하나밖에 없다.
점 P가 | x(t) | = 1 을 찍고 그대로 돌아오는 경우이다.
그런데 선지에서 묻고있는건 | x(t) | < 1 인 경우이므로
방향전환은 두번 일어나는 것임을 알 수 있다.
P점이 출발하여
방향 전환을 두 번 하고 다시 원점으로 돌아오려면
중간에 원점을 무조건 한번 지나야한다.
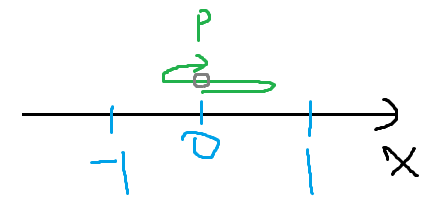
보다시피 회색 동그라미 친 지점이 원점을 지나는 순간이다.
따라서 ㄷ(o)
따라서 답은 3번
15 )
문제가 길어서 두장으로 나눠 올립니다.


빈칸추론이 15번..?
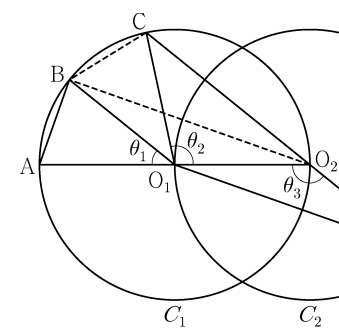
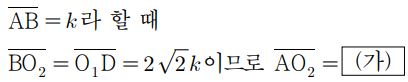
선분 AO₂ 는 원 C₁ 의 지름이므로
각 ABO₂ 는 직각이다.
따라서 삼각형 ABO₂는 직각삼각형이고
피타고라스 정리를 이용하면
k² + 8k² = 9k² = (AO₂)²
따라서 AO₂ 의 길이는 3k 이며
따라서 f(k) = 3k 이다.
삼각형 ABO₂ 가 직각삼각형이고
각 변의 길이의 비를 알고 있으므로 cos값을 구할 수 있다.

따라서

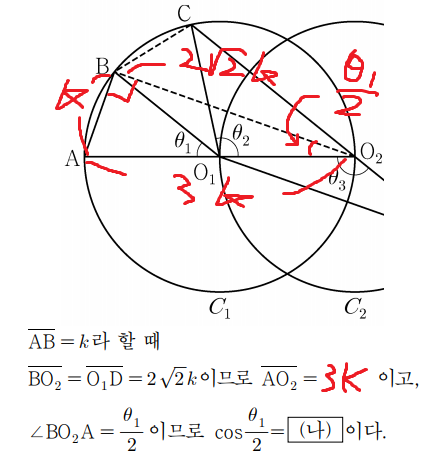
그냥 다알려준다.
O₂C 의 길이를 ℓ 이라 하겠다.
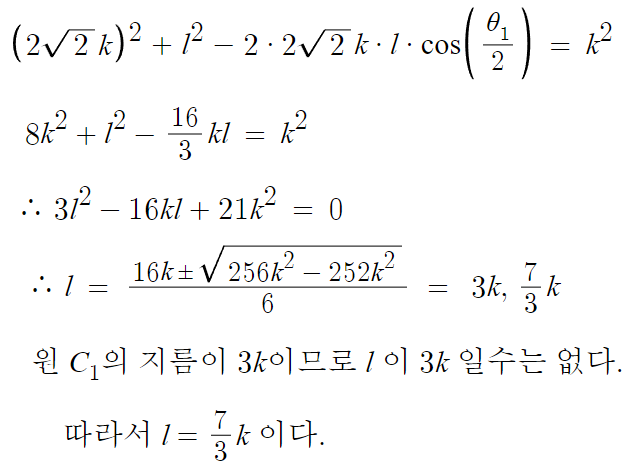
따라서 g(k) = 7k/3 이고
이제 대입하고 계산하면 끝난다.
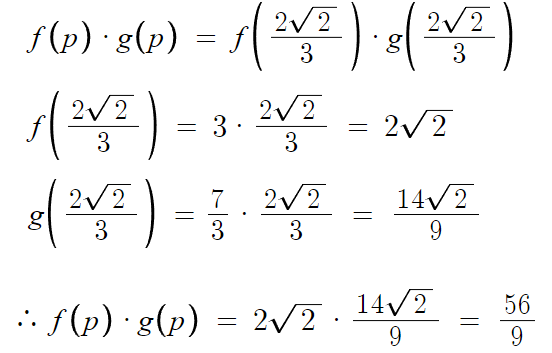
따라서 답은 2번
'2022학년도 기출 해설 > 2022학년도 수능 해설' 카테고리의 다른 글
| 2022학년도 수능 수학 확률과통계 23번~30번 해설 (1) | 2021.12.28 |
|---|---|
| 2022학년도 수능 물리II 해설 (0) | 2021.11.23 |
| 2022학년도 수능 물리I 해설 (0) | 2021.11.21 |
| 2022학년도 수능 수학 미적분 23번~30번 해설 (0) | 2021.11.19 |
| 2022학년도 수능 수학 공통 16번~22번 해설 (0) | 2021.11.19 |



