
홀수형 기준입니다.
혹시 본인이 못 푼 문제인데
어떻게 푸는건지 궁금해서 이 글을 보는거라면
이 글을 보지 말것.
남이 풀어주는걸로는 실력이 늘지 않는다.
풀긴 풀었는데 풀면서 100%확신하진 못하고 약간 찜찜했거나
다른 풀이도 있을까 해서 찾아보는거라면
매우 환영이다.
원하시는 문제로 바로 가고싶으면
N번 문제로 가고싶다면
N )
이 형태로 검색하시면 됩니다.
예를들어 17번으로 가고싶으면 17 )
쉬운건 빠르게 넘어가면서
비약 하나도 없이 풀어보겠습니다.
16 )

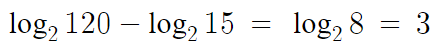
따라서 답은 3
17 )

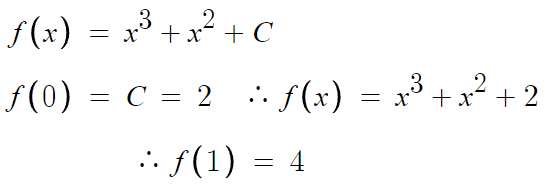
따라서 답은 4
18 )

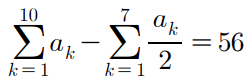
이 식의 양변에 2를 곱하면 아래 식이 완성된다.
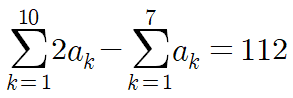
이제 위 식을
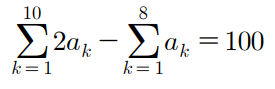
이것과 뺄셈연립하면
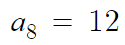
따라서 답은 12
19 )

증가한다 = 도함수가 음수가 아니다.
따라서 실수 전체의 집합에서 f'(x)≥0 임을 보이면 된다.

따라서 a의 최댓값은 6이고
답은 6
20 )

(나) 조건의 식에 x=0을 대입하면
f(1)-0 = b
f(1) = 1이므로 b=1이다.
문제에서 f(x)는 실수 전체의 집합에서 미분가능하다 했으므로
(나) 조건에서 주어진 식의 양변을 미분하면
f'(x+1) - f(x) - xf'(x) = a
x=0 을 대입하면 f'(1) - f(0) - 0 = a
f'(1) = 1, f(0) = 0 이므로 a=1 이다.
여기서 f'(1)이 왜 1인가?
닫힌구간 [0,1]에서 f(x)=x 이므로
닫힌구간 [0,1]에서 f'(x) = 1 이고
따라서 f(x)의 x=1 에서의 좌미분계수는 1임이 자명하다.
근데 f(x)는 미분가능한 함수이므로
x=1 에서의 우미분계수도 1으로 같을것이기 때문에
f'(1) = 1 인 것이다.
따라서 a=1, b=1을 대입하여 (나) 조건의 식을 다시 쓰면 아래와 같다.
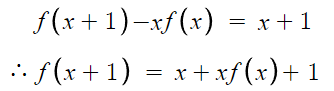
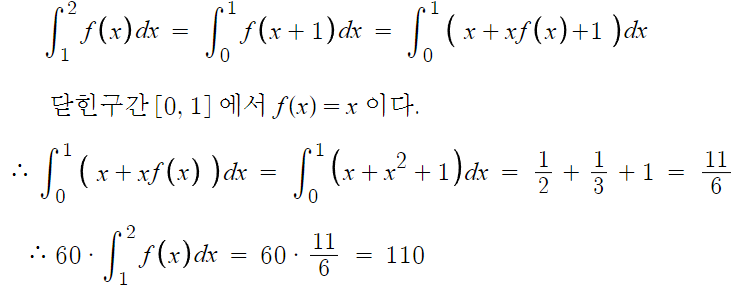
따라서 답은 110
21 )

수열 a_n은
첫째항의 크기가 2이고
갈수록 크기가 두배씩 커진다.
규칙이 단순한데다가
(다) 조건상 10번째항까지만 알면 되기 때문에
이 수열의 각 항이 될 수 있는 값들을 직접 써보고
그것들을 이용해 조건들을 풀어나가보겠다.

(가) 조건과 (나) 조건을 만족하는 경우를 모두 쓴것이다.
각 항의 값의 크기는 알고 부호만 결정해주면 된다.
이제 (다) 조건을 보자.
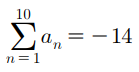
1항부터 10항까지 전부 더한게 -14라고 한다.
여기서 핵심은
1항부터 10항까지 전부 더한게 음수라는 점이다.
만약 a_10 = 1024 이고
나머지는 전부 음수라고 해보자.
그러면 수열 a_n은
범위 n≤9 에서
첫째항이 -2이고 공비가 2인 등비수열이 된다.
이 등비수열의 1항부터 9항까지의 합을 구해보자.
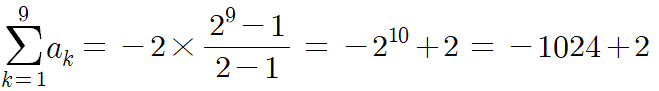
1024는 10번째 항의 값 아닌가?
따라서 이 수열의 제1항부터 제10항까지 전부 더하면 +2가 나오게 된다.
즉 a_n의 10번째 항인 a_10 의 값이 양수면
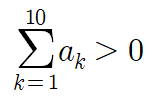
아무리 1항부터 9항까지 모두 양수라 한들
1항부터 10항까지 더한 값이 무조건 양수가 나오기 때문에
a_10 = -1024 여야 한다.
같은 논리로 a_9 의 부호도 결정할 수 있다.
만약 a_9가 음수 즉 -512 라면
a_1부터 a_8까지 전부 양수라고 해도
a_1부터 a_8까지 전부 더해도
a_9 의 음수 크기를 상쇄시킬정도의 힘이 되지 않기때문에
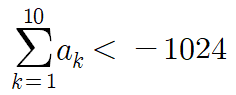
이렇게 될 것이다.
즉 (다) 조건을 만족시키기 위해서는
적당히 작은 음수여야되는데
너무 큰 음수인 것이다.
수식으로 증명하자면 다음과 같다.
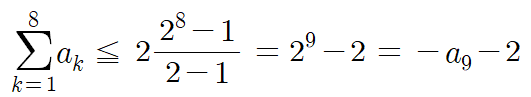
a_1부터 a_8까지 전부 더한게 -a_9 - 2 보다 작다.
따라서 a_9가 음수라면 (다) 조건을 만족할 수 없기 때문에
a_9는 양수이고 그 값은 512이다.
이 이후에도 같은 논리를 적용하면
a_8 = 256
a_7 = 128
a_6 = 64
...
이런 식으로 될텐데
그럼 a_10 빼고 전부 양수면
a_1부터 a_10까지 전부 더한것의 값이 최대가 될것이다.
이 최대가 되는 지점을 기준으로 잡고 (다) 조건에 맞는 수열 a_n을 결정할것이다.
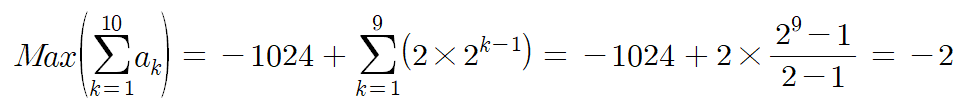
따라서
a_1 = 2
a_2 = 4
a_3 = 8
a_4 = 16
a_5 = 32
a_6 = 64
a_7 = 128
a_8 = 256
a_9 = 512
a_10 = -1024
일때, 1항부터 10항까지 더한것의 값은
가능한 음수의 결과값중 최댓값이 되며
그 값은 -2이다.
근데 (다) 조건상 1항부터 10항까지 모두 더한것은 -14여야한다.
근데 아까 가능한 음수의 결과값중 최댓값인게 -2라 했으니
이 최댓값에서 12를 빼줘야한다.
즉 12만큼 덜 더해져야한다.
음수의 결과값중 최대가 나오는 상황에서 12만큼 덜 더하면 되는거다.
12만큼 덜 더했다는건
원래 6만큼 더해줬었다면 반대로 6만큼 빼주면 되는거다.
즉 a_x + a_y = -6 이 되게 하는 자연수 x, y 조합을 찾으면 되고
그 x와 y는 1과 2이다.
a_1 = -2이고 a_2 = -4 인 것이다.
원래 +2+4+... 였던게
-2-4+... 가 되니까
결과적으로는 12만큼 덜 더한게 되는것이다.
따라서 정리하자면
a_1 = -2
a_2 = -4
a_3 = 8
a_4 = 16
a_5 = 32
a_6 = 64
a_7 = 128
a_8 = 256
a_9 = 512
a_10 = -1024
따라서 a_1 + a_3 + a_5 + a_7 + a_9는
-2 + 8 + 32 + 128 + 512 = 678
따라서 답은 678
22 )

우선 f(x)는 최고차항의 계수가 양수인 삼차함수니까
가능한 개형은 이 두가지로 나눌 수 있다.

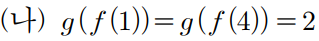
(나) 조건에 의하면
f'(x)=0이 닫힌구간 [t, t+2] 에서 갖는 실근의 개수가
2 인 경우도 존재해야하는데
첫번째 개형은
f'(x) = 0인 지점이 한군데밖에 없기때문에 그러지 못한다.
따라서 f(x) 의 개형은 아래와 같다.
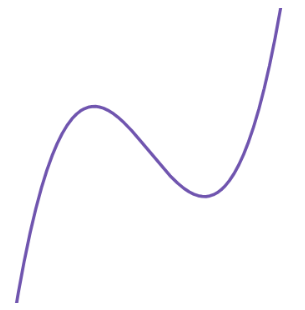
이제 (가) 조건을 풀어보겠다.
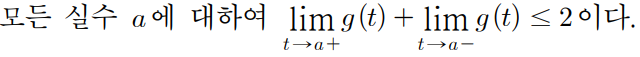
이것이 의미하는건
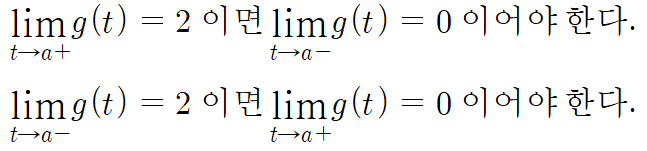
이제 아까 (나)조건에서 힌트를 얻어서 대략적으로 추론했던 f(x)의 개형에서
a값을 변화시키면서
이것이 의미하는 바가 무엇인지 찾아보자.
모든 실수 a에 대해 성립해야하기 때문에
a에 상관없이 무조건 성립하게 하는 특별한 조건을 찾아낼 수 있을 것이다.
1. a → -∞ 인 경우 (매우 작은 경우)
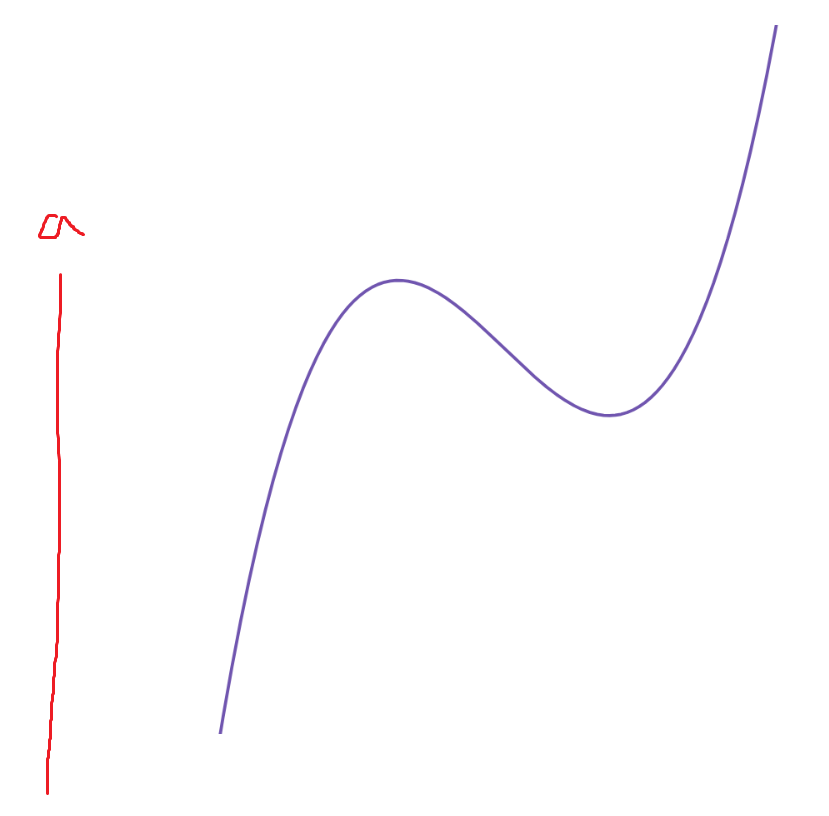
우선 f(x)는 삼차함수기 때문에
g(t)의 최댓값은 2이며
최솟값은 0이다.
a가 매우 작은 경우에는
[t, t+2] 에서 f'(x)=0 인 지점이 존재하지 않으므로
g(t)=0 이다. 따라서 이 경우엔 f(x)가 무엇이냐에 상관없이
(가) 조건이 무조건 성립한다.
2. a→∞ 인 경우 (매우 큰 경우)
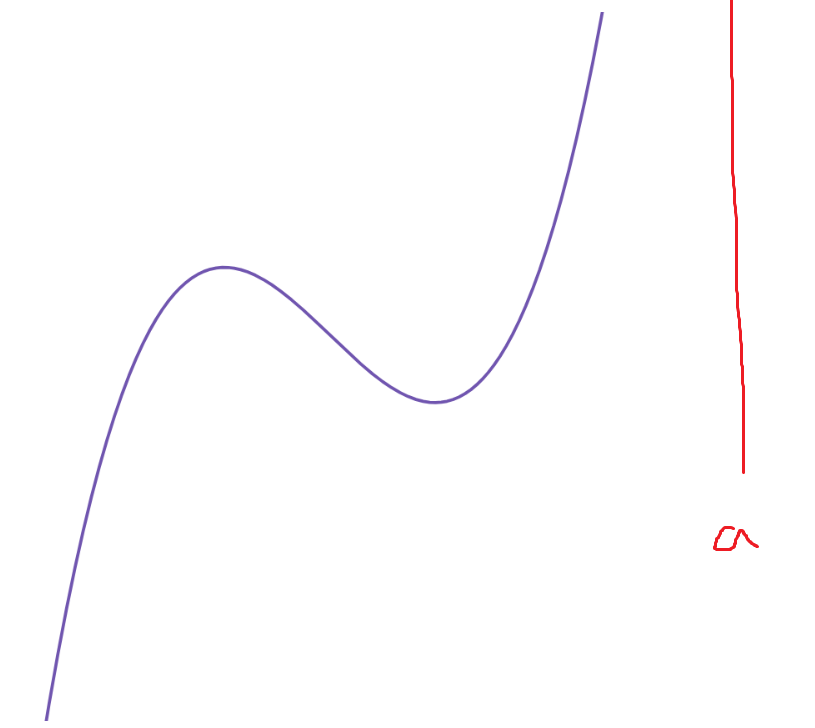
같은 논리로 g(t) = 0 이기때문에
항상 (가) 조건을 성립시킨다.
3. a>극소지점 인 경우
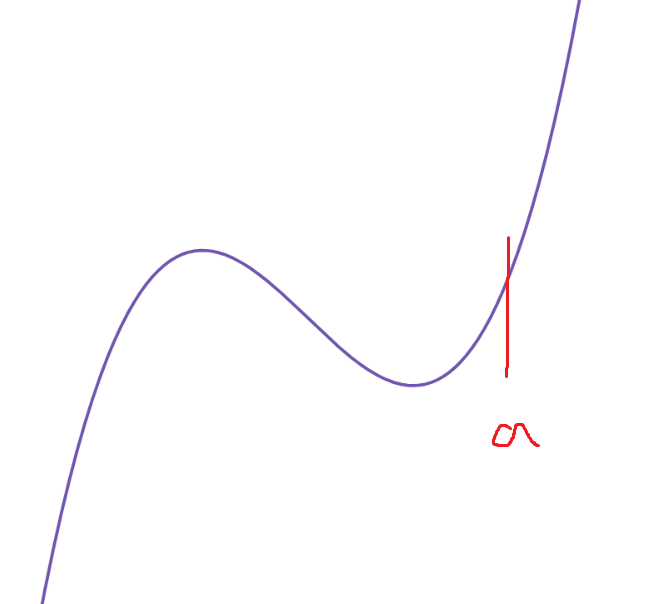
극대지점 이후 f'(x)=0이 성립하는 곳이 없으므로
g(t)=0 이며 항상 (가)조건을 성립시킨다.
4. 극소지점<a<극대지점 인 경우
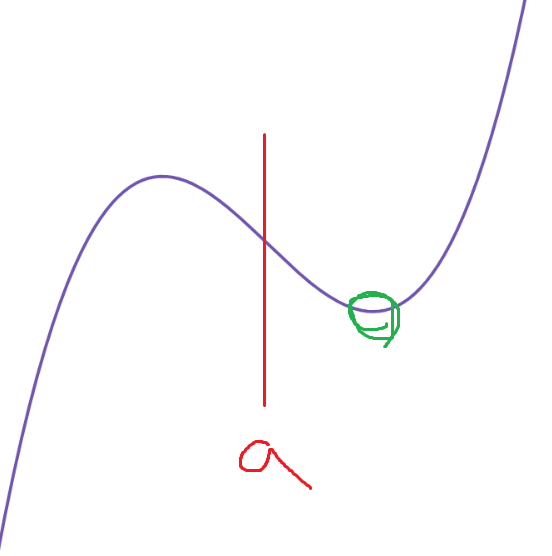
이건 녹색 동그라미 친 지점에서 f'(x)=0 이므로
g(t) = 1 이다.
따라서 (가)조건을 항상 성립시킨다.
5. a=극대지점 인경우
여기부터가 중요하다.

녹색 동그라미 친 지점에서 f'(x) = 0 이다.
여기가 왜 중요하냐면
g(t)의 t=a에서의 좌극한값과
g(t)의 t=a에서의 우극한값이
다르기 때문이다.
왜냐면
좌극한이라면 t=a를 포함해서 구하는게 g(t)이고
우극한이라면 t=a를 포함하지 않고 구하는게 g(t)이다.
즉 g(t)의 t=a에서의 좌극한은 최소 1이고
오른쪽 녹색 동그라미 친 지점과의 거리에 따라
2가 될수도 있다.
만약 극대점과 극소점 사이의 거리가 2보다 작다면
g(t)의 t=a에서의 좌극한값은 2가 되는것이다.
만약 g(t)의 t=a에서의 좌극한이 2라면
g(t)의 t=a에서의 우극한이 1이 되어버려서
(가) 조건을 만족하지 못한다.
즉 여기서 다음과 같은 결론을 얻을 수 있다.
' 극대점과 극소점 사이의 x좌표 간격은 2 이상이다 '
6. a<극대지점 인경우
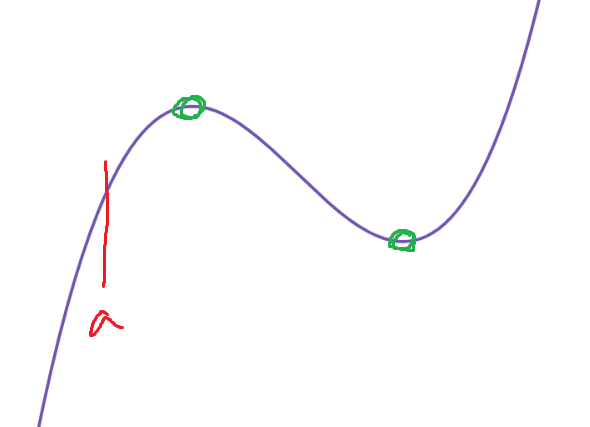
아까 a의 5번째 구간에서
극대점과 극소점 사이의 간격은 2 이상임을 알았으니
g(t)의 t=a에서의 좌극한값의 최댓값도 1이고
우극한값의 최댓값도 1이다.
따라서 (가)조건이 성립한다.
여기까지 (가) 조건을 풀어본것이다.
결론은 다음과 같다.
' 극대점과 극소점 사이의 x좌표 간격은 2 이상이다 '
이제 (나) 조건을 본격적으로 풀어보자.
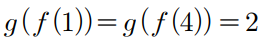
이것의 의미는
g(t)=2가 되도록 하는 t값이 존재한다는 것이다.
즉 [t,t+2] 에서 f'(x)=0 인 지점이 2개가 되기 위해서는
'극대점과 극소점 사이의 x좌표 간격이 2 이하'여야 한다.
아까 (가) 조건에서 구한
' 극대점과 극소점 사이의 x좌표 간격은 2 이상이다 '
와 합치면 다음과 같은 결론을 얻을 수 있다.
' 극대점과 극소점 사이의 x좌표 간격은 2이다 '
그리고 이를 토대로 몇가지 더 알 수 있는데
극대점과 극소점 사이의 x좌표 간격이 2이므로
g(t) = 2가 되려면
t는 무조건 극대점이어야 한다.
따라서 f(1) = f(4) = f(x)의 극대점의 x좌표
여기서 f(x)의 극대점의 x좌표를 α 라 하면
f(x)를 다음과 같이 쓸 수 있다.
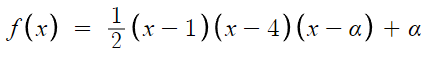
그리고 극대점의 x좌표가 α 라면
극소점의 x좌표는 α+2 이므로
f'(x)를 다음과 같이 쓸 수 있다.
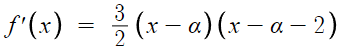
위에 써놓은 f(x)를 미분한게 이 식이 되어야 하므로
미분하면
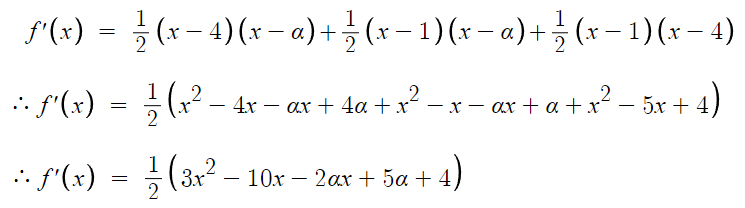
여기에 x=α를 대입하면 0이 나와야 하니까
대입하면
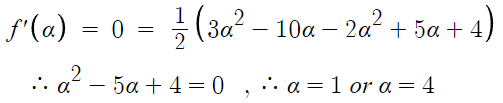
α=1 또는 α=4 이다.
이제 마지막으로 안 쓴 조건 하나가 남아있는데
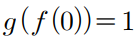
이것이 의미하는 바는
닫힌 구간 [ f(0), f(0)+2 ] 에서 f'(x)=0인 x값이 하나 존재한다는 뜻이므로
f(0)은 α-2 이상이며 α+2 이하이다. 단 f(0)≠α 이다.
라는 뜻이다.
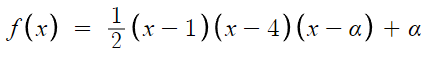
따라서 여기에 0을 대입하면
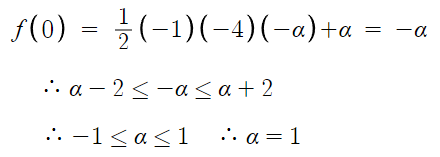
따라서 f(x)의 추론이 완료되었다.
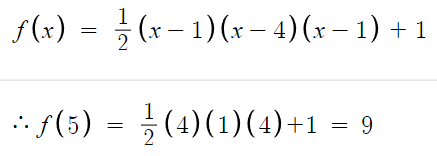
따라서 답은 9
'2022학년도 기출 해설 > 2022학년도 수능 해설' 카테고리의 다른 글
| 2022학년도 수능 수학 확률과통계 23번~30번 해설 (1) | 2021.12.28 |
|---|---|
| 2022학년도 수능 물리II 해설 (0) | 2021.11.23 |
| 2022학년도 수능 물리I 해설 (0) | 2021.11.21 |
| 2022학년도 수능 수학 미적분 23번~30번 해설 (0) | 2021.11.19 |
| 2022학년도 수능 수학 공통 1번~15번 해설 (0) | 2021.11.19 |



