
- 개요 -
이번에 어떤걸 구하는거냐면

이걸 구할거다.
5+x 라는 다항식과
x-3 이라는 다항식을
곱셈연산하려면 어떻게해야하느냐 이다.
즉 다항식끼리 곱셈연산하는 방법을 배울것이다.
우선 전개하라는게 무슨말인가?
예를들어 3(a+b) 를 전개하라 하면
분배법칙에 따라서 3a+3b 이다.
이런식으로 할거아닌가?
즉 3(a+b) = 3a+3b 이다.
근데 여기서 3(a+b) 라는 다항식은
항이 몇개인가? 1개이다.
즉 3(a+b)는 단항식이다.
3a+3b 라는 다항식은
항이 2개이다.
즉 3a+3b는 항이 2개인 다항식이다.
따라서
전개한다는 말의 뜻은
항이 한개인 단항식을
항이 여러개인 다항식으로 바꾼다.
즉 곱꼴로 나타내어져 있는것을
합꼴로 나타내는것이 전개이다.
추가로, 이를 반대로 하는 과정이 바로 '인수분해'이다.
인수분해는 합꼴로 나타내어져 있는 다항식을
곱꼴로 나타내어져 있는 단항식으로 바꾸는것이기 때문이다.
- 다항식의 곱셈에 대한 성질 -
우선 알아야할게 있다.
너무 당연한거라 그냥 그런가보다 하면 된다.

즉 여기서 말하고자 하는건
다항식의 연산도 여태 숫자로 하던대로 그냥 하면 된다.
2×3이나 3×2나 결과값이 같으니 교환법칙이 성립하듯이
다항식에서도 A×B나 B×A나 결과값이 같다는거다.
당연한거지만 이걸 알고는 있어야한다.
이 뒤에 나오는
다항식의 곱셈법이나 다항식의 곱셈 공식은
전부 이걸가지고 증명하기 때문이다.
- 다항식의 곱셈법 -

그래서 전개를 어떻게하는거냐면
원리는 매우 간단하다.
1. 일단 각각의 다항식들을 내림차순으로 정리한다.
2. 분배법칙을 이용해 전개한다.
3. 동류항끼리 모아서 정리한다.
하나씩 해보자.
일단 각각의 다항식들을 내림차순으로 정리한다.
내림차순 정리하는 이유는
보기 편해서이다.
굳이 안해도 되지만
나중에 식이 복잡해지면 실수하기 쉽다.
5+x를 내림차순정리하면 x+5
x-3은 이미 내림차순정리 돼있으니 x-3
따라서 여기까지한 결과는

그다음 분배법칙을 이용해 전개할것이다.
근데 뭔가 싱겁지않은가?
원래 전부터 분배법칙으로 전개해왔는데
뭐가 특별하다는건가?
그 말이 맞다.
왜냐면 3(a+b) 를 전개하면 3a+3b 라는것 정도는
중학교수학이고 분배법칙 이용해서 된다는걸 알거다.
근데 3도 다항식이다.
즉 이미 다항식 × 다항식 꼴을 다루는법을 알고있었던것이다.
다만 여태 했던건 단항식 × 다항식 이었던것 뿐이고
이젠 다항식 × 다항식 으로 확장하겠다는것이다.
즉 그냥 중등수학의 확장 개념이다.
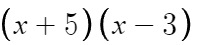
여기서
A = x+5
B = x
C = -3
이라고 잡고 분배법칙을 적용하면
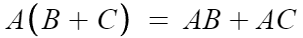
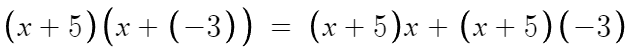
여기서 (x+5)x 와 (x+5)(-3) 에 대해 분배법칙을 또 써주면
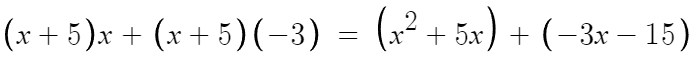
이렇게 다항식의 덧셈연산 까지 오게되고
여기부터 이제 동류항끼리 모아서 정리하면 된다.
동류항끼리 모아서 정리하기
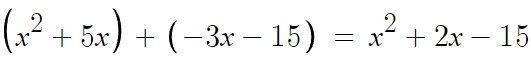
여기서 정리라는건 내림차순으로 정리한다는것까지 포함이다.
내가 지금 제시한 예시는 운이 좋게도 알아서 정리되어있어서 그냥 계산하면 된다.
따라서 결론은

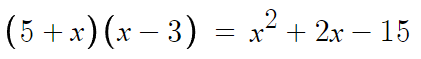
- 예제문제로 중간점검 -
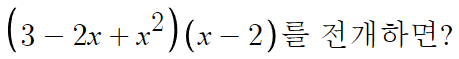
1. 각각의 다항식을 내림차순으로 정리한다.
3-2x+x² 를 내림차순 정리하면
x²-2x+3
x-2를 내림차순 정리하면
x-2
따라서 여기까지 한 결과는
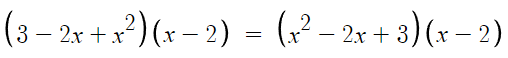
2. 분배법칙을 이용해 전개한다.
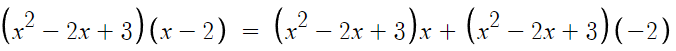
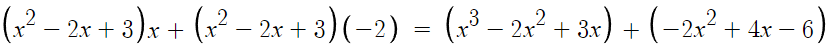
3. 동류항끼리 모아서 정리한다.
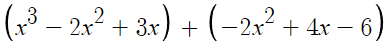
두 다항식에서 최고차항 = 3차항인 x³
최고차항을 갖고있는 다항식이 x³-2x²+3x 니까
x³-2x²+3x 의 동류항을 찾아서
최고차항부터 차수를 하나씩 내리면서 계산할것이다.
x³의 동류항 : 없음. 0
따라서 3차항의 계산결과는
x³이다.
-2x²의 동류항 : -2x²
따라서 2차항의 계산결과는
-4x²이다.
3x의 동류항 : 4x
따라서 1차항의 계산결과는
7x이다.
x³-2x²+3x에서 상수항은 0이다.
0의 동류항 : -6
따라서 상수항의 계산결과는
-6이다.
이제 내림차순 정리하면
x³ - 4x² + 7x - 6

따라서 답은
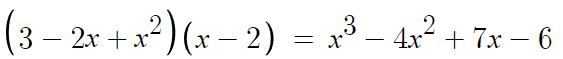
- 곱셈 공식 -
들어가기전에 중요한거 알려주자면
절대 여기 공식을 암기하려들지 말자.
어차피 다항식의 곱셈연산의 원리를 알고있다면
공식같은거 하나도 몰라도 된다.
여기서 나오는 문제는
이 공식을 암기해서 푸는게 아니라
하도 자주 나오는 형태라서 반복하다보니 자연스럽게 외워지는거다.
외워서 한다. 가 아니라 하다보니까 외워지던데? 가 되어야 한다.
그냥 다항식의 곱셈연산인데
좀 자주나오거나 결과가 특이한 형태라서 특별대우해주는것 뿐이다.
1. 완전제곱식
어떤 다항식을 제곱한 식을 완전제곱식이라 한다.
(a+b)² 은 (a+b) 라는 다항식을 제곱한것이다.
(a-b)² 은 (a-b) 라는 다항식을 제곱한것이다.
이것들을 전개하면 아래와 같다.
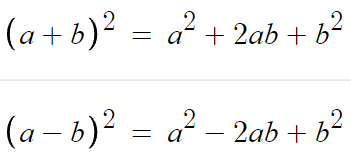
증명은 직접 해보는것도 좋은데
일단 보여주겠다.
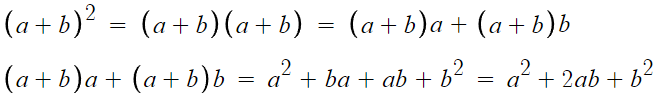
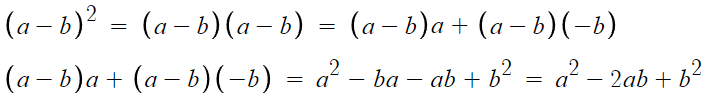
보다시피 그냥 다항식의 곱셈이다.
게다가 어렵지도 않다. 그니까 외우지 말자.
한 5번만 직접 공식을 백지에다가 써서 증명해보자.
하고나면 외우려고 노력하지 않아도 이미 외워져있다.
2. 합차공식
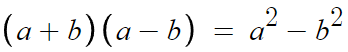
증명과정은 다음과 같다.
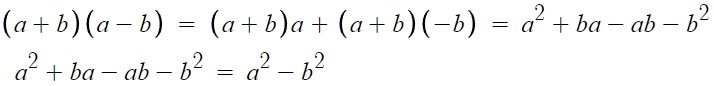
이게 어렵나?
대단한 테크닉이 들어갔나?
전혀 아니다. 그니까 외우지 말자.
3.
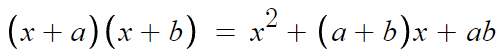
증명과정은 다음과 같다.
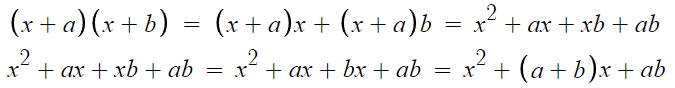
4.
솔직히 여기부터는 나도 안외우고다닌다.
하지만 보면 풀수있다. 나는 다항식의 연산 원리를 이해하고있기 때문에
어떤 공식이 나와도 스스로 풀어낼수 있는거다.

증명과정은 다음과 같다.
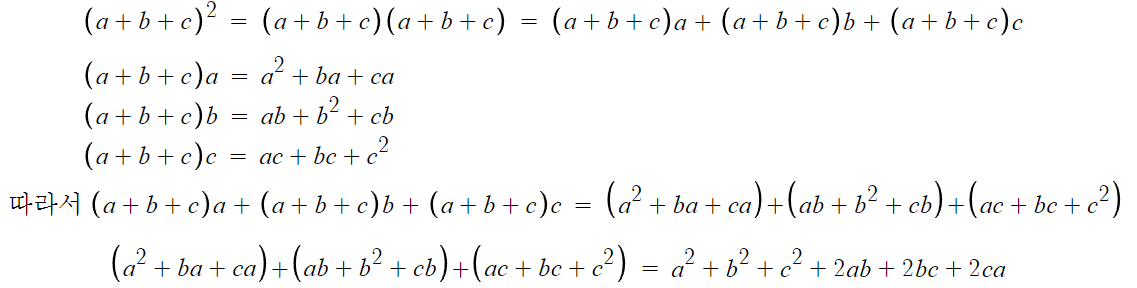
조금 길긴 하지만 어려운건 아니다.
5.
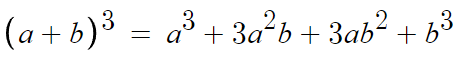
증명과정은 다음과 같다.
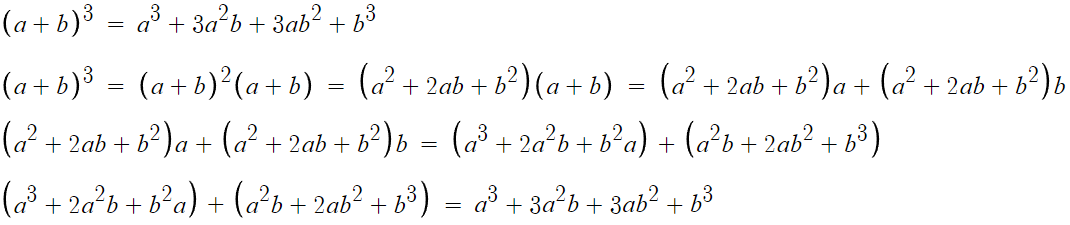
- 심화 : 곱셈공식의 변형 -
가장 흔히 나오는 두가지를 다루겠다.
1. 완전제곱식의 변형
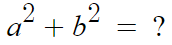
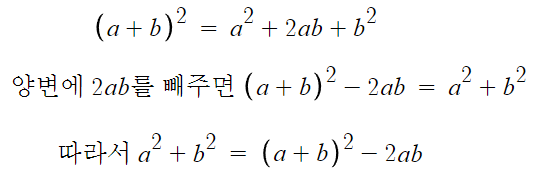
보통 어떤문제에 쓰냐면
a+b=3 이고 ab = -10 일때, a²+b²의 값은?
이런 문제가 나오면
a²+b² = (a+b)² - 2ab 니까
a²+b² = 3² - 2×(-10) = 9+20 = 29
이렇게 풀면 된다.
2.
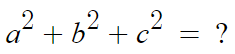

보통 어떤문제에 쓰냐면
a+b+c=2, ab+bc+ca=-1 일때, a²+b²+c²의 값은?
이런 문제가 나오면
a²+b²+c² = (a+b+c)² - (2ab+2bc+2ca) = 2² - 2(-1) = 4+2 = 6
이렇게 풀면 된다.
대체 이런 풀이를 어떻게 생각해낼수있냐고 할수 있는데
문제가 다 이런식으로밖에 안나와서
몇문제 풀어보면 감을 잡는다.
- 예제 -
1 )
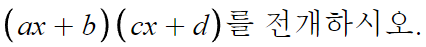
이거 사실 곱셈공식에 있는내용인데
스스로 한번 증명해보라고 여기다 넣었다.
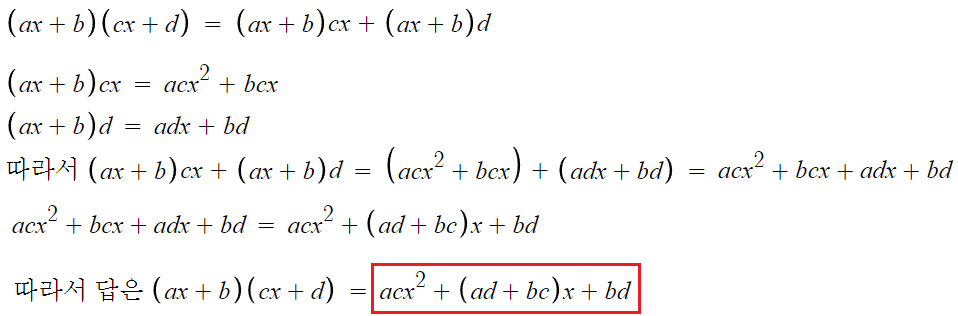
답은 acx² + (ad+bc)x + bd
2 )

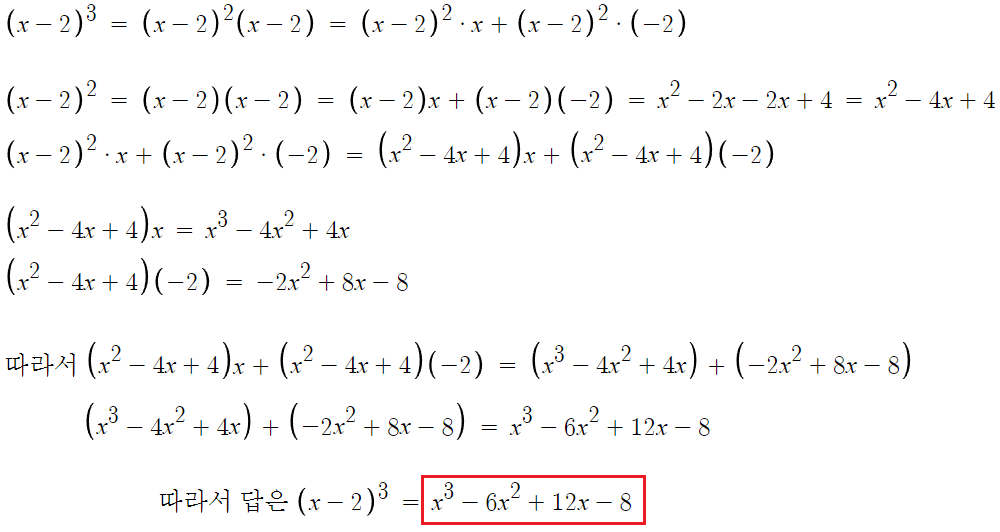
공식으로 풀어도 된다.
(a+b)³ = a³ + 3a²b + 3ab² + b³
이 공식에서
a=x , b=-2 니까
대입하면
x³ + 3x²(-2) + 3x(-2)² + (-2)³
따라서 답은 x³-6x²+12x-8
3 )
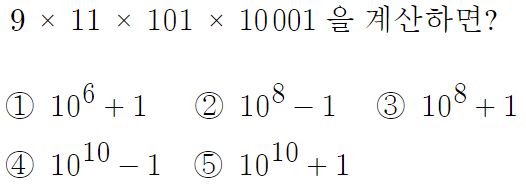
처음 공부하는사람은 당황스러울법한 문제인데
약간의 스킬이 필요해서그렇다.
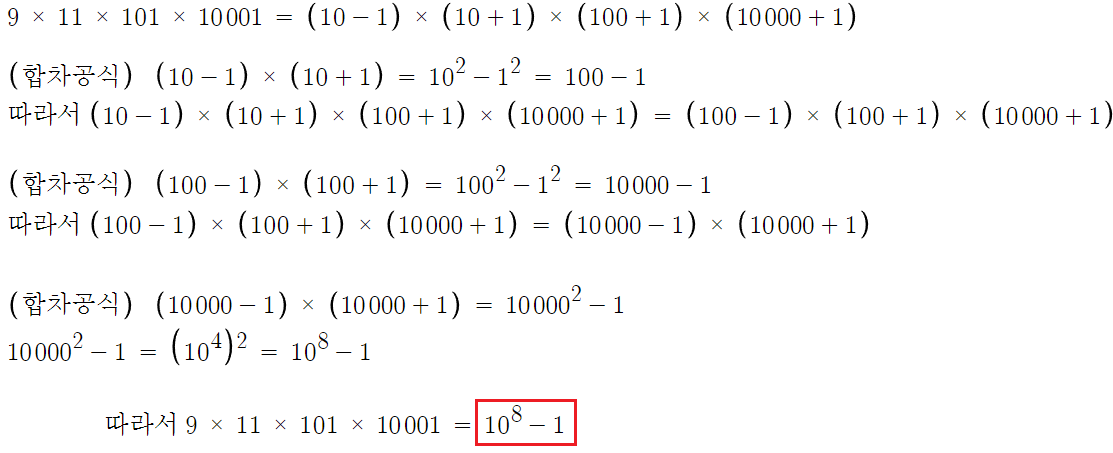
아직 익숙하지 않아서 합차공식을 못외웠어도
(10-1) × (10+1) = (10-1)×10 + (10-1)×1
(10-1)×10 + (10-1)×1 = 100-10+10-1 = 100-1
이런식으로 계속하면 풀수있다.
따라서 답은 2번
4 )
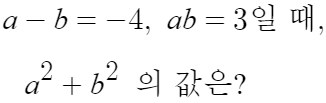
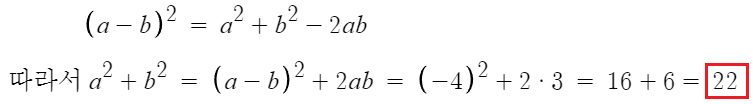
따라서 답은 22
'수학(상) > I. 다항식' 카테고리의 다른 글
| 조립제법 (2) | 2022.01.07 |
|---|---|
| 나머지정리와 인수정리 (0) | 2022.01.05 |
| 항등식과 미정계수법 (0) | 2022.01.04 |
| 다항식의 연산 #3 - 다항식의 나눗셈 (0) | 2022.01.04 |
| 다항식의 연산 #1 - 다항식의 덧셈과 뺄셈 (0) | 2021.12.28 |



