
- 개요 -
사실 다항식의 나눗셈에서
직접 나눠보지 않아도
몫과 나머지까지 빠르게 구할수있는 방법이 존재한다.
그게 바로 조립제법이다.
단, 고등수학에서는 '일차식'으로 나눌때만 조립제법을 쓰도록 되어있다.
이차식 이상으로 나눌때는 또 이거나름대로 복잡하기때문에 고등수학에서는 다루지 않는다.
- 조립제법이란? -
조립제법(組立除法)
제법 : 나누는 방법
조립 : 부품들을 조립한다 와 같은한자
즉 조립제법이란 무언가를 조립해서 나누는 방법이며
뭘 조립할거냐면 계수들을 조립할것이다.
즉 조립제법 : 계수들을 이용해서 나누는 방법
좀더 구체적으로는
계수들을 특정하게 배열(組)하여
알맞게 조립제법의 형태를 세우고(立)
이 형식으로 나눗셈(除)을
수행하는 방법(法)
- 조립제법 직접 해보자 -
일단 하는것부터 보여주겠다.
원리 설명은 그 뒤에 할것이다.

일단 원래 우리가 하던 방법으로 해보자.

구할수는 있지만 귀찮다.
그래서 어떻게 할거냐면
일단
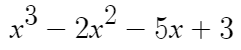
이 식을
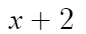
이 식으로 나눌것이다.
따라서
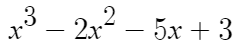
얘는 '나눗셈 당할' 다항식이다.
나눗셈 당할 식과
나눗셈을 할 식을 구별해야한다.
1. '나눗셈 당할 식'을 내림차순 정리한다.
이번건 이미 내림차순 정리되어있으니 생략
2. 내림차순 정리되어있는
'나눗셈 당할 식' 에서
최고차항의 계수부터 차수를 하나씩 내리면서
계수들을 일렬로 나열한다.
무슨말이냐면
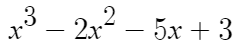
이 식은 삼차식이며
삼차항은 x³ , 따라서 삼차항의 계수는 1
이차항은 -2x² , 따라서 이차항의 계수는 -2
일차항은 -5x , 따라서 일차항의 계수는 -5
상수항은 3
이제 1, -2, -5, 3 을 일렬로 나열한다.

3. 아래 그림과같이
ㄴ자로 긋는다.
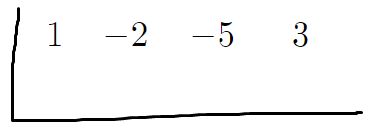
이따가 숫자를 한줄 더써야하기때문에
아래에 여유공간을 남겨놓고 그어야된다.
4. ㄴ자로 그어놓은거 왼쪽에다가
나누고자 하는 일차식이 0이 되도록 하는 x값을 넣는다.
그리고 나누고자 하는 일차식의 계수를 그림과 같이 표시한다.
예를 들어 이번문제에서는
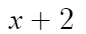
이걸로 나눌거니까 -2를 넣어주면 된다.
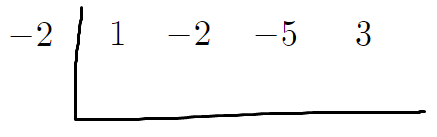
5. ㄴ자 안에 있는 것은
나눗셈 당할 식의 계수인데,
이 계수중 맨 앞의 것(최고차항인 것)을
아래로 그대로 내려서 쓴다.
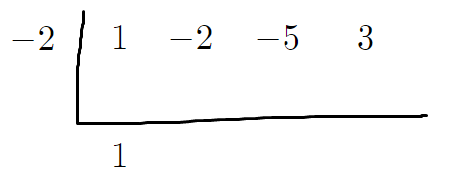
6. 아까 ㄴ자 왼쪽에 적어놓은 수인 -2랑
아까 아래로 내려버린 1을 곱해서
그 결과값을 아래 그림과 같이 적는다.
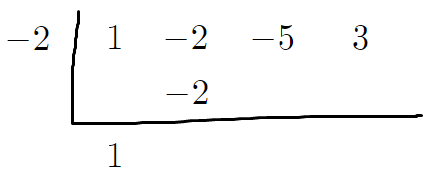
7. 동그라미친 두 수를 더해서
그 결과값을 아래에 적는다.
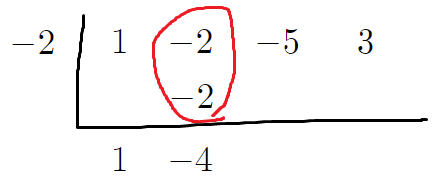
8. 6~7번 과정을 반복한다.
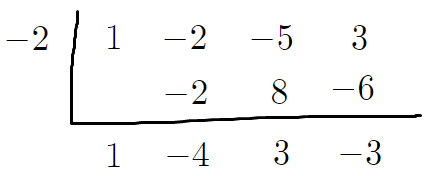
그러면 이렇게 될텐데
아래에 적힌게 몫과 나머지이다.

가장 오른쪽것이 나머지이고
그 외에 왼쪽에있는거가 몫의 계수이며,
계수가 내림차순으로 정렬되어있는것이다.
몫의 계수가 1 , -4 , 3 이라 나왔으니
몫은 x²-4x+3 인것이다.
따라서 몫과 나머지는 다음과 같다.
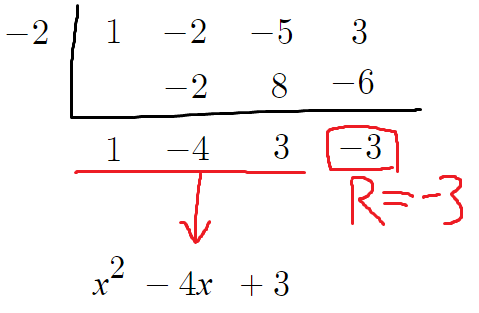
몫은 x²-4x+3 이고
나머지는 -3 이다.
이 과정을 gif로 한번 요약해주겠다.
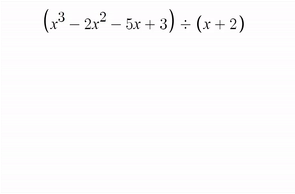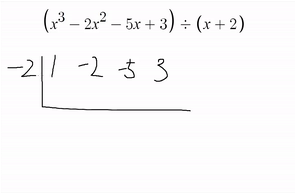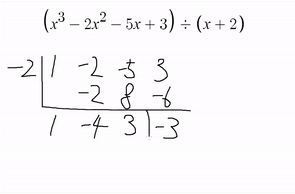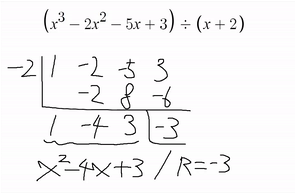
주의할 것은
계수가 0이어도 일단 0이라고 써줘야한다.
무슨 말이냐면, 아래 나눗셈도 연습겸 해서 조립제법으로 해보자.
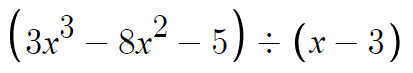
여기서 '나눗셈 당할 식'은
3x³-8x²-5 이다.
조립제법을 쓰기 위해 계수만 적어보자.
삼차항의 계수 3
이차항의 계수 -8
'일차항의 계수 0'
상수항 -5
따라서 3 , -8 , 0 , -5 이렇게 나열해야한다.
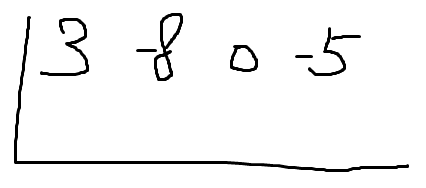
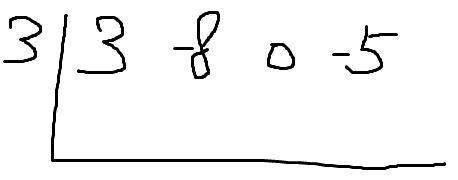
이제 나눌 일차식이 x-3 이니까
x-3을 0으로 만드는 x값을 왼쪽에 써준다.
그런 x값은 3이다.
이제 나눗셈 당할 식의 계수중
맨앞의것을 그대로 내린다.
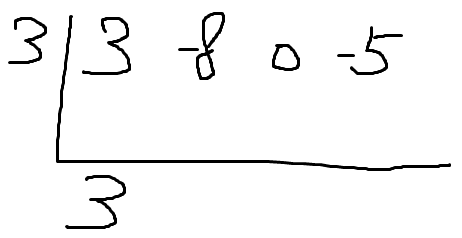
왼쪽에 적어놓은 수와 아까 내린 수를 곱해서 그림과같이 적는다.
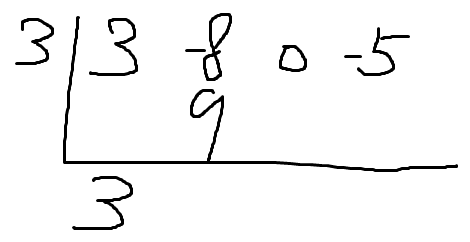
-8 + 9 = 1 이고
따라서 1을 아래에 적은다음 이 과정을 반복하면 된다.

따라서 몫은 3x²+x+3 이고
나머지는 4 이다.
- 심화 : 나누고자 하는 일차식의 계수가 1이 아닌경우 -
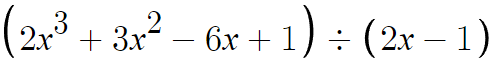
하던대로 하면 되는데,
한가지 과정을 추가로 해줘야한다.

일단 여기까진 하던대로 한다.
근데 2x-1 로 나눈다는건
2x-1 = 2(x-1/2) 이기 때문에
이대로 몫을 구하면
우리가 원하는 몫이 아니라
그 몫의 2배의 값이 나오게 된다.
무슨 말이냐면, 항등식을 세워보자.
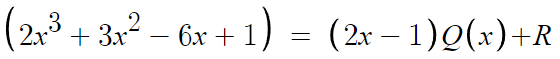
일단 이건데, 2x-1 = 2(x-1/2) 니까

이렇게 바꿔쓸수도 있다.
여기서 문제는,
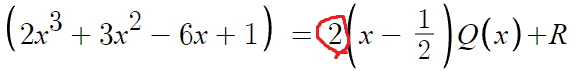
이 2때문에 Q(x)의 값을 제대로 구할수가 없다.
왜냐면 일단 저 2를 그냥 없애고 계산해보자.
2(x-1/2) 로 나누는게 아니라
x-1/2 로 나눠보자는거다.

이제 조립제법을 써보려 하면 문제가 있음을 알게되는데,

아까 2x-1로 나누는것과 조립제법의 형태가 똑같기때문에
결과값이 똑같이 나와버린다.
즉 나누는 일차식의 계수에 상관없이 몫이 똑같이 나와버린다.
이러면 999(x-1/2)로 나눠도 결과값이 똑같이 나와버릴것이다.
말이 되지 않는다.
그래서 한가지 작업을 더 해줘야 한다.
어떤 식을 2(x-1/2) 로 나눈다는건
(x-1/2)를 2배 한걸로 나눈다는건데
그럼 나눗셈의 몫 결과값은
(x-1/2) 로 나눈것의 1/2배가 되어야하지 않겠는가?
따라서 몫을 그냥 계산하면
나누는 일차식의 일차항의 계수를 곱한것만큼 크게 나와버리니까
일단 조립제법을 쓴다음
일차식의 일차항의 계수로 나눠버리면
우리가 원하는 몫이 나올것이다.
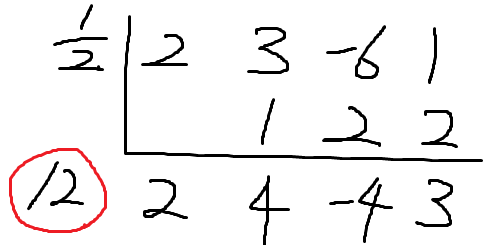
빨갛게 동그라미쳐놓은 부분은 처음보는걸텐데
조립제법에서
나누는 일차식에서 일차항의 계수를
저렇게 표현한다.
12가 아니라 /2 이다.
끝나고 2로 나눠달라는 뜻이다.
일단 나머지는 3이다.

이 식을 보면
나누는 일차식에서 일차항의 계수와 나머지는 상관없음을 알수 있다.
그리고 몫은
2x²+4x-4 가 아니라
나누는 일차식의 일차항의 계수가 2 이니까
전체적으로 2를 나눠주면
x²+2x-2 가 몫이다.
따라서 몫은 x²+2x-2 , 나머지는 3 이다.
- 조립제법의 원리(증명) -
정말 신기한데 원리는 더신기하다.
사실 조립제법의 원리는 고등학교과정이 아니라서
고등학생이라면 원리는 몰라도 되고
그냥 암기해서 써도 되는데
원리가 궁금할 사람들을 위해 적어놓는다.
최대한 고1이 이해할수있게 쉽게 간다.
어려운거니 이해안된다고 자책할필요는 없다.
n차 다항식이 있다고 해보자.
n차 다항식이라는건 최고 차수가 n차 라는거다.
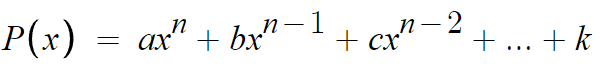
이 n차 다항식을 P(x)라 하겠다.
a, b, c, ... , k 는 계수이다.
a : n차항의 계수
b : n-1 차항의 계수
c : n-2 차항의 계수
...
이를 반복하여 상수항까지
...
k : 상수항
그리고 이 n차 다항식 P(x)를
일차식 f(x)로 나눈다고 하겠다.

A, B는 계수이다.
여기서 몫을 Q(x)라 하고,
나머지를 R이라 하면
다음과 같은 항등식을 세울수 있다.
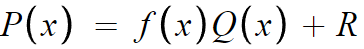
P(x)와 f(x)를 대입해서 다시 쓰면
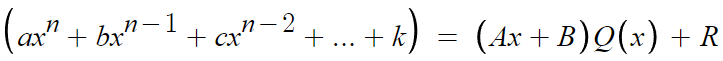
그리고, n차식을 일차식으로 나눴으므로
몫은 n-1차식이다.
따라서 Q(x)를 다음과 같이 쓸수 있다.
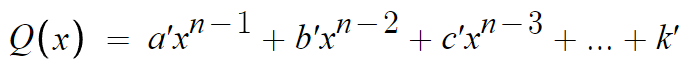
Q(x)까지 대입해서 위의 항등식을 다시쓰면
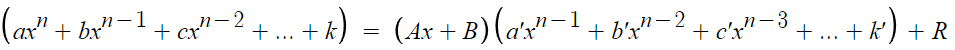
이제 우리는
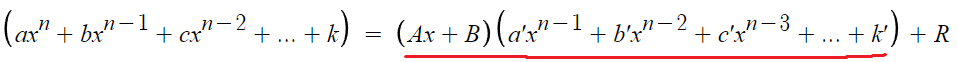
밑줄친 부분을 전개할것이다.
밑줄친 부분을 전개하면 아래와 같이 된다.

이걸 또 대입해서 항등식을 다시쓰면

항등식이기 때문에
a = Aa'
b = Ab'+Ba'
c = Ac'+Bb'
...
k = Bk'+R
이라는 결론을 얻는다.
이걸 왜구한거냐면
이제 조립제법을 한번 써보자.
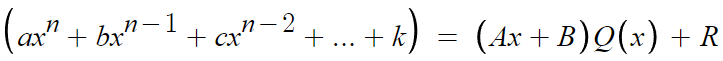
나눗셈 당할 다항식은 P(x) 이니까
P(x)의 계수만 뽑아서 내림차순으로 나열하면
a, b, c, ... , k
이렇게 되고
나눌 일차식은 Ax+B 이니까
Ax+B=0 을 만족시킬 x값을 왼쪽에 적어주면되고
그런 x값은 x=-B/A 이다.

여기서 조립제법을 쓰기 전에
아까 구한 관계식을 대입해주자.
a = Aa'
b = Ab'+Ba'
c = Ac'+Bb'
...
k = Bk'+R

이제 조립제법을 써보자.

아름답게도 Ba', Bb' 와 같이 보기싫은것들이
계속 계산되면서 0이 되고
나누는 일차식에서 일차항의 계수가 A니까
여기서 최종적으로 A로 나눠주기까지 하면
a', b', c' 와 같이 아주 간단하고 규칙적이게만 남는것을 볼수 있다.
이건 우연이 아니라, 그렇게 될수밖에 없게 계산 과정을 짜놓은것이다.
계산 결과가 이렇게 되도록 하는게 조립제법의 원리이다.
이렇게 얻어내는 결론적인 몫과 나머지는
일단 나머지는 R인거 바로 보이고
몫은 내가 아까 적어뒀던 식을 보면
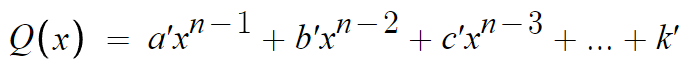
너무 아름답게도 딱 들어맞는다.
- 예제 -
1 )

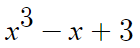
우선 얘가 '나눗셈 당할 식' 이다.
이 식의 최고차항은 3차이고
3차항의 계수는 1
2차항의 계수는 0
1차항의 계수는 -1
상수항은 3
따라서 최고차항부터 나열하면
1 0 -1 3
이다.
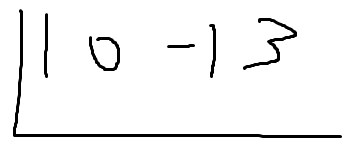
여기까지 한거다.
그리고 x-2로 나눌거니까
x-2=0이 되도록 하는 x값을 왼쪽에 써준다.
그런 x값은 2이다.
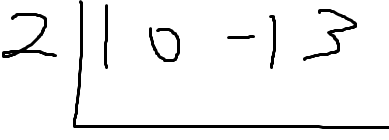
그다음 '나눗셈 당할 식' 에서
최고차항의 계수인 1을 그대로 내린다.
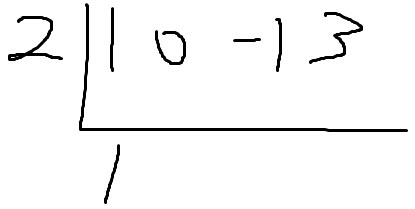
그다음 아까 내린 1과
왼쪽에 써놓은 2를 곱해서 아래와같이 쓴다.
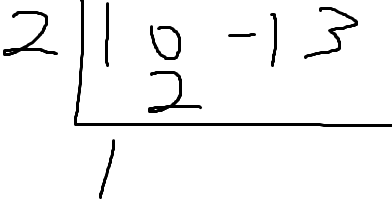
그다음 이차항의 계수인 0과
아까 쓴 2를 더해서 아래에 쓰고,
이 과정을 반복한다.
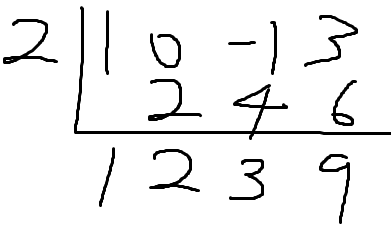
따라서 답은
몫 : x²+2x+3
나머지 : 9
2 )

우선 일차식으로 나누는거니까
조립제법을 쓸수있을거고
그러면 Q(x)를 구할수 있을거다.
그리고 Q(x)를 또 일차식으로 나눈다고 하니까
이것도 조립제법쓰면 최종적인 몫을 구할수 있을것이다.
우선 Q(x)부터 구해보자.
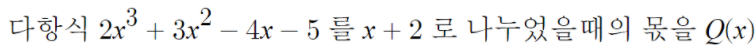
문제에서 조립제법 쓰라니까 조립제법으로 풀자.
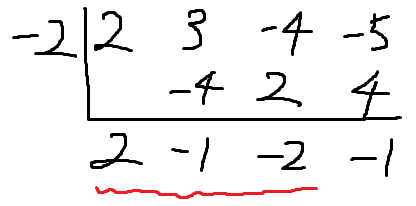
밑줄친것이 바로 Q(x)의 계수이다.
따라서 Q(x)는
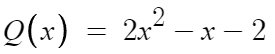
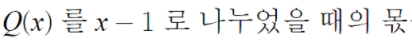
또 조립제법쓰면 되겠다.

따라서 구하고자 하는 몫은 2x+1 이다.
따라서 답은 2x+1
3 )

조금 난이도있는 문제이다.
조립제법을 처음 공부하는사람에게는 어려운 문제일것이다.
이 문제는 조립제법을 쓸수도 있고,
안쓸수도 있다.
쓰는게 더 빠르니까 일단 쓰는 풀이부터 보여주겠다.
- 조립제법을 이용한 풀이 -
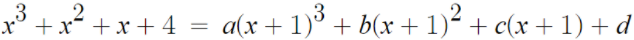
우선 이 식이 항등식이므로
x에 어떤걸 대입해도 성립한다.
우변에 x+1이 많으니까 x=-1 을 대입하고 싶어진다.
x=-1을 대입하면
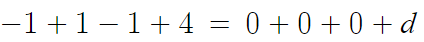
따라서 d=3
지금까지 한건
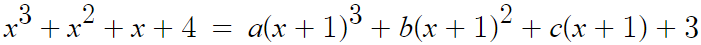
이제 a, b, c의 값을 구하면 되는데
우변에 x+1이 반복되는게 좀 수상하지 않은가?
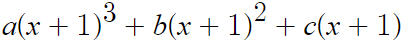
이 부분은 전부 (x+1) 을 '인수'로 가지고 있다.
즉 공통으로 갖는 인수이므로
곱셈의 분배법칙을 응용하면 (x+1)을 밖으로 끌어낼 수 있다.
곱셈의 분배법칙 : A(B+C) = AB+AC 인데
이걸 반대로 하는 과정인것이다.
AB+AC 에 공통으로 A가 곱해져있으니
A(B+C) 로 나타내자는것이다.
이게 수학에서 전반적으로 정말 많이 쓰이는 논리이기 때문에
(x+1)이 공통이니까 일단 밖으로 끌어내고싶고
그러지 않으면 불편할 정도로 익숙해지게 연습해야한다.
그렇게 하고나면 식이 아래와같이 된다.
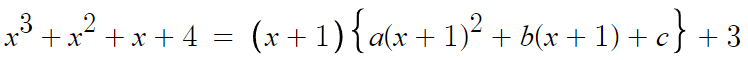
이렇게 끌어내고 나니까
나눗셈에서의 항등식과 형태가 똑같아졌다.
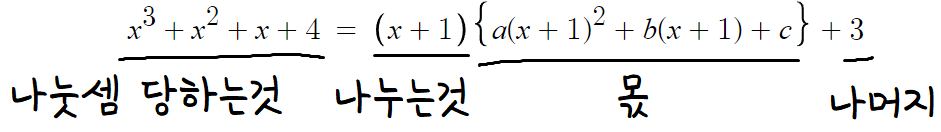
마침 나누는것도 일차식이다.
조립제법을 쓰고싶다.
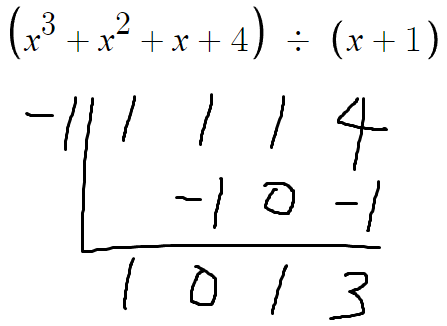
따라서 몫의 계수는 1, 0, 1 이다.
아직 흥분하면 안된다.
a=1 b=0 c=1 아니다.
여기서 구한 1, 0, 1은
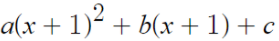
이 식에서의 계수이다.
ax²+bx+c 였다면 a=1, b=0, c=1 맞는데
x가 아니라 x+1 이기때문에
일단 전개해서
동류항끼리 정리해줄 필요가 있다.
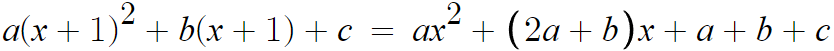
전개 과정은 생략
그럼 이제 결론은
a=1
2a+b = 0
a+b+c = 1
a=1 이므로 2a+b = 2+b = 0
따라서 b=-2
따라서 a+b+c = 1-2+c = 1
따라서 c=2
따라서 a=1, b=-2, c=2, d=3 이므로
abcd = -12
따라서 답은 -12
- 조립제법을 이용하지 않는 풀이 -
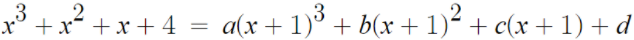
이 식이 항등식이므로
x에 어떤 값을 대입해도 성립한다는것 하나로 푼다.
미지수가 a, b, c, d 4개니까
관계식을 4개를 세우면
식 4개를 연립해서 a, b, c, d의 값을 구할수 있을것이고
그러면 답도 구할수 있을것이다.
아까 조립제법쓰는 풀이에서와 같은 논리로
x=-1 을 대입하면 d=3 임을 알수있다.
이번엔 x=0을 대입해보자.
여기서 뭘 대입할지는 푸는사람 자유이다.
난 x=0을 대입하는게 계산이 간단해질거같아서 x=0을 대입하는것이다.
x=0을 대입하면
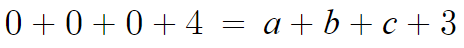
따라서 a+b+c = 1 이다.
이번엔 x=1을 대입해보겠다.
x=1을 대입하면
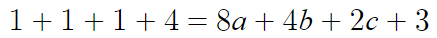
따라서 4a+2b+c = 2 이다.
관계식 하나만 더쓰면 연립해서 a, b, c를 구할수 있다.
이번엔 x=2를 대입해보겠다.
x=2를 대입하면

따라서 9a+3b+c = 5 이다.
a+b+c = 1
4a+2b+c = 2
이 두 식과 연립하면 a, b, c를 구할수 있다.
우선 9a+3b+c = 5 에서 4a+2b+c = 3 을 뺄셈연립하면
5a+b = 3
4a+2b+c = 2 에서 a+b+c = 1 을 뺄셈연립하면
3a+b = 1
5a+b = 3 에서 3a+b = 1 을 뺄셈연립하면
a = 1
3a+b=1 이므로 a=1을 대입하면 b=-2
a+b+c=1 이므로 a=1, b=-2를 대입하면 c=2
따라서 a=1, b=-2, c=2, d=3
따라서 abcd = -12
따라서 답은 -12
'수학(상) > I. 다항식' 카테고리의 다른 글
| 인수분해 (0) | 2022.01.07 |
|---|---|
| 나머지정리와 인수정리 (0) | 2022.01.05 |
| 항등식과 미정계수법 (0) | 2022.01.04 |
| 다항식의 연산 #3 - 다항식의 나눗셈 (0) | 2022.01.04 |
| 다항식의 연산 #2 - 다항식의 곱셈 (0) | 2021.12.29 |



