
- 개요 -
이번에 할 것은
'모든 x에 대하여 p이다.'
'어떤 x에 대하여 q이다.'
이런 명제를 다룰거고
두 '조건' 사이에 특별한 관계가 있으면
그걸 충분조건이나 필요조건 같이 부르는데 이것도 다룰것이다.
- '모든' 이 있는 명제 -
여기서 다루는 명제는
조건 p 가 있다고 하면,
'모든 x에 대하여 p이다.'
이 명제는 참인가? 거짓인가? 를 판별할것이다.
근데 판별하기 전에, 의문점이 있을 수 있다.
p는 조건이고, 조건은 명제가 아닌데
어떻게 저 문장은 명제가 될 수 있는가?
'모든 x에 대하여~'
이 문구가 들어가있어서
저건 명제가 된다.
'모든 x에 대해, 조건 p를 만족하는가?' 를 묻는것이다.
만약 그렇다면 참인거고, 그렇지 못한다면 거짓인거다.
예시를 들어주겠다.
조건 p: x²>-1 이다.
'모든 실수 x에 대하여 p이다.'
이건 참인가?
모든 실수 x에 대하여 라는건
x값을 아무거나 넣어도 p 조건을 만족하는지 보라는거다.
실제로 x값을 아무거나 넣어도
조건 p인 x²>-1 을 만족한다.
따라서, 이때 이 명제는 참이다.
이번엔 거짓인 예시를 들어주겠다.
조건 p: x²>0 이다.
'모든 실수 x에 대하여 p이다.'
이건 참인가?
이게 참이라면, 실수 x값을 아무거나 넣어도 p 조건을 만족해야한다.
그런데, x=0 에서는 x²=0 이므로
p 조건을 만족하지 못한다.
따라서, 이때 이 명제는 거짓이다.
하나라도 p 조건을 만족하지 못하는경우가 발견되면 거짓이다.
'모든 x에 대하여~' 라고 했기 때문이다.
이에 대한 수학적인 표현은 아래와 같다.

말이 좀 어렵게 적혀있는것처럼 보이는데, 사실 쉽다.
조건 P와 전체집합 U가 똑같으면 참이고,
그렇지 않으면 거짓이라는 뜻이다.
이는 당연한것이,
모든 x에 대하여 라는건
전체집합 U에서 x값 아무거나 뽑으라는거고
아무거나 뽑아도 p를 만족하려면
P가 전체집합 U와 똑같은경우
즉 P=U 인 경우를 제외하면 없다.
당연히 P는 U의 부분집합이니 P가 U보다 집합이 클수는 없다.
- '어떤' 이 있는 명제 -
여기서 다루는 명제는
조건 p 가 있다고 하면,
'어떤 x에 대하여 p이다.'
이 명제는 참인가? 거짓인가? 를 판별할것이다.
여기서도 역시 p는 조건이지만
'어떤 x에 대하여~'
이 문구가 들어가있어서
저건 명제가 된다.
'어떤 x에 대해, 조건 p를 만족하는가?'
그니까 '조건 p를 만족하게하는 x값이 존재하는가?'
를 묻는것이다.
만약 그렇다면 참인거고, 그렇지 못한다면 거짓인거다.
예시를 들어주겠다.
조건 p: x²≤0 이다.
'어떤 실수 x에 대하여 p이다.'
이건 참인가?
어떤 x에 대하여 라는건
p 조건을 만족하는 x값이 존재하는지 보라는거다.
실제로 x=0 에서는 x²=0 이므로
조건 p인 x²≤0 을 만족한다.
따라서, 이때 이 명제는 참이다.
x=0을 제외한 모든 x에 대하여 조건 p를 만족하지 못하지만,
아무튼 만족하는 x가 하나라도 존재하므로 참이다.
'모든' 이 있는 명제와 반대다.
만족하는 x가 하나라도 있으면 참이 되는것이다.
이번엔 거짓인 예시를 들어주겠다.
조건 p: x²<-1 이다.
'어떤 실수 x에 대하여 p이다.'
이건 참인가?
이게 참이라면, p 조건을 만족하는 x값이 존재해야한다.
그런데, x값으로 어떤 실수를 넣어도
p 조건을 만족하지 못한다.
따라서, 이때 이 명제는 거짓이다.
p 조건을 만족하는 실수 x가 하나도 없으므로 거짓이다.
이에 대한 수학적인 표현은 아래와 같다.

조건 P와 공집합 Ø가 다르면 참이고,
같으면 거짓이라는 뜻이다.
이는 당연한것이,
어떤 x에 대하여 라는건
전체집합 U에서 어떤 특정한 x값을 뽑았을때
p를 만족하게 하려면, P가 공집합만 아니면 된다.
공집합만 아니면 전체집합 어딘가에서 p를 만족하는 x를 찾을것이기 때문이다.
따라서, 이게 거짓이려면
P가 공집합 Ø와 똑같은경우
즉 P=Ø 인 경우를 제외하면 없다.
- '모든' 이나 '어떤' 이 있는 명제의 부정 -
사실, '모든' 이나 '어떤' 이 있는 명제는
여기때문에 다들 헷갈려하는것이다.
이걸 헷갈리는 이유는 하나밖에 없는데, 그냥 외워서그렇다.
조금만 생각해보면 너무 간단하게 해결되는 문제이다.
'모든 x에 대하여 p이다' 를 부정하려면
모든 x에 대하여 ~p 이다 라고 하면 되는건가?
결론부터 말하자면 그렇지 않다.
왜냐면, 명제의 부정이란게 뭐였는지 상기해보자.
어떤 명제 p에 대하여
p가 아니다. 를 p의 부정이라 한다.
즉, 어떤 명제가 있으면
그것이 참이거나, 그것의 부정이 참이거나
무조건 둘중 하나 해야하며,
둘다 참이거나 둘다 거짓인 경우는 없다.
예를 들어주겠다.
p : 이 사람은 남자이다.
이 명제의 부정은 ~p 이다.
~p : 이 사람은 여자이다.
모든 사람은 남자 아니면 여자이기 때문에,
p와 ~p 중 하나는 무조건 참이다.
물론 p가 참이면 ~p는 거짓이며,
p가 거짓이면 ~p는 참이다.
p와 ~p가 둘다 거짓이면
'이 사람은 남자도 아니고 여자도 아니다.'
라는 문장이 되며, 무조건 거짓이게 된다.
이런 경우는 존재할수 없다는뜻이다.
같은 맥락으로 p와 ~p가 둘다 참일 수 없다.
'이 사람은 남자이면서 여자이다.'
이것도 무조건 거짓이다.
부정이란게 뭐였는지를 잊지 말아야하며,
이걸 가지고 푸는거다.
문제를 보여줄테니 같이 풀어보자.
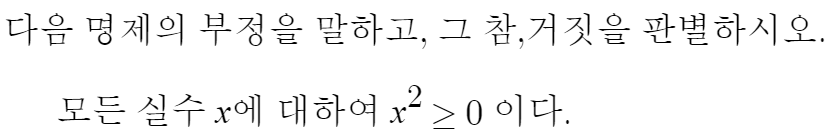
모든 실수 x에 대하여 x²≥0 이다. 를 명제 p라고 하자.
그러면 이 명제의 부정은 ~p 가 된다.
~p를 말하라는게 문제인데,
어떻게 말하면 될까?
우선 p가 참이라는게 무슨뜻인지 좀 쉽게 설명하자면
'p가 참이다 = 모든 실수 x에 대하여 x²≥0 을 만족한다.'
즉, '실수 x로써 그 어떤것을 가져와도
x²≥0 을 만족하지 않는 x는 존재하지 않는다.'
즉, x²<0 을 만족하는 실수 x는 존재하지 않는다.
이게 p다.
부정을 구할거면 이걸 부정하면 된다.
'x²<0 을 만족하는 실수 x가 존재한다.'
라고 하면 부정한거다.
명제의 부정의 정의에 의하면
x²<0 을 만족하는 실수 x는 존재하거나, 존재하지않거나
무조건 둘중 하나는 만족할거기 때문이다.
그니까, ~p : x²<0을 만족하는 실수 x가 존재한다.
이를 처음에 제시된 명제처럼 형태를 갖춰 다시 쓰면
~p : '어떤 실수 x에 대하여 x²<0 을 만족한다.'
그리고 이건 참인가?
참이 아니다. x²<0 을 만족하는 실수 x는 존재하지 않는다.
따라서, 이 명제의 부정은 거짓이다.
추가로, 제시된 명제가 참이냐고 물으면
이 명제의 부정이 거짓이므로 이 명제는 참입니다.
라고까지 할수 있어야한다.
- 충분조건과 필요조건 -
이건 쉬운데 헷갈리기 쉬우니 연습이 필요하다.

p이면 무조건 q이다?
p 이기만 하면 q를 항상 만족시키기에 충분하다는거고
따라서 p는 q이기 위한 '충분조건'이 된다.
즉, p, q의 진리집합을 각각 P, Q라 하면
P⊂Q 이다.
즉, Q가 P를 담고있으면
p는 q이기 위한 충분조건이라 한다.
주의할건, p→q 가 참이라 해서
그 역인 q→p 가 항상 참인건 아니다.
그래서 이럴때는
q는 p이기 위한 '필요조건' 이라 하는거다.
p이기 위해 q가 필요하긴 한데,
이것만으로는 p를 항상 만족한다 장담할순 없으니
필요조건이라 하는것이다.
여기서 역인 q→p 까지 동시에 만족하는 경우엔
p이면 무조건 q이며, q이면 무조건 p이다.
이런 경우에서 p는
q이기 위한 '필요충분조건' 이라고 한다.
물론 반대로 q도 p이기 위한 필요충분조건이라 해도 된다.
이런 경우는 'P=Q' 인 경우밖에 없다.
p는 q이기 위한 충분조건이므로 P⊂Q 이다.
근데 q도 p이기 위한 충분조건이므로 Q⊂P 이다.
따라서, 필요충분조건이려면 P=Q 이어야한다.
- 수학적 증명법 -
학습목표 : 우리가 여태 공부했던 수학 공식, 정리들을
수학적으로 엄밀히 증명할 수 있게된다.
여기는 보통 '증명해보시오.' 라고 문제를 출제하지는 않고
제시되는 수학적 증명과정을 보고 이해하는지,
어떤식으로 증명하는건지 이해하고있어서
빈칸을 뚫어놓으면 채워넣을수 있는지
이정도로 물어본다.
개인적으로 아주 재미있어하는 곳이라서,
시험에서 안낸다고 대충할게 아니라
본인들이 직접 학문적인 호기심을 갖고
여러가지 공식이나 정리들을 증명해봤으면 좋겠다.
처음엔 잘 안될것이다. 해본적이 없으니까 어디부터 시작해야할지도 모를거다.
아주 쉽고 간단한거라도 좋다. 스스로 증명해보면 까먹을 일이 없으며,
까먹었다 해도 스스로 증명해서 써먹으면 된다.
그래서 이걸 하면 실제로 수학실력 상승에 많은 도움이 되며,
이게 이런거였어? 하면서 놀라는 일이 많다.
소재를 떠올리지 못할 사람들을 위해
몇가지 예를 들어주자면,
1. 왜 두 음수의 곱은 양수인가?
2. 서로 수직인 두 직선의 기울기의 곱은 왜 -1인가?
3. xy≠0 이면 x≠0 이고 y≠0 이다. 그 이유는?
4. 왜 원 밖의 한 점에서 원에 그은 접선은 항상 두개인가?
5. 왜 √(2) 는 무리수인가?
6. 왜 이차방정식의 판별식이 양수이면 서로다른 두 실근을 갖는가?
이것중 홀수번인 1, 3, 5번을 풀어줄테니
짝수번은 스스로 풀어보기 바란다.
참고로, 이 블로그 글들 뒤져보면 다 있다.
- 1. 왜 두 음수의 곱은 양수인가? -
우선 이걸 증명하려면 ' (-1) × (-1) = 1 ' 임을 증명하면 된다.
모든 음수는 양수에 -1을 곱해서 만든거기 때문이다.
예를 들어, -3 × -4 = (-1×3) × (-1×4) = (-1)×(-1)×12
(-1) × (-1) = 1 임을 증명하겠다.
우선, 1 = 1 이라는 등식은 자명하게 항상 성립한다.
등식의 성질을 이용한다.
위 식에서 우변의 1을 이항하면
1 + (-1) = 0 이다.
양변에 -1을 곱하면 1×(-1) + (-1)×(-1) = 0
모든 실수는 1을 곱하면 자기자신이 나온다.
따라서 1×(-1) = -1 이고, 이를 위 식에 대입하면
-1 + (-1)×(-1) = 0 이고
-1을 이항하면, (-1)×(-1)=1 이다.
따라서 음수 × 음수 = 양수 이다.
Q. E. D. (Quod Erat Demonstrandum, 증명종료)
- 3. xy≠0 이면 x≠0 이고 y≠0 이다. 그 이유는? -
보통 어떤걸 증명할때
= 기호가 아니라, ≠ 기호로 연결되어있는 식들은
대개는 이 명제의 '대우' 가 참임을 증명하는게 더 쉽다.
우리가 명제 단원에서 배운걸 써먹겠다는거다.
어떤 명제의 대우가 참이면, 그 명제는 참이다.
이건 중요한거니까 알아두자.
물론 전에 배우고왔으니 알긴하겠지
근데 증명과정에서 써먹을수 있어야한다는 말이다.
저 명제의 대우는
'x=0 이거나 y=0 이면 xy=0 이다.'
이게 참임을 증명하는것이 더 쉽다.
x=0 이라면, y의 값에 관계없이 xy=0 이다.
y=0 이라면, x의 값에 관계없이 xy=0 이다.
따라서, x=0 이거나 y=0 이면 xy=0 이다.
대우가 참이므로,
원래 명제인 'xy≠0 이면 x≠0 이고 y≠0 이다.' 는 참이다.
Q. E. D.
여기서 증명할 때 주의할것은,
논리적으로 빈틈이 전혀 없게 엄밀하게 해야한다.
xy=0 이려면 x=0 이거나 y=0 이어야 하니까 저건 참입니다
라고 적으면 맞긴한데, 직관적인 비약이 있었다는 말이다.
xy=0 이려면 왜 x=0 이거나 y=0 이어야 하는지를 보여야한다.
물론 이건 아주 쉬운거라 직관적으로 바로 보이지만,
직관으로 도저히 따라갈 수 없을 정도의 고차원적인 명제라면 어떻게 증명할건가?
- 5. 왜 √(2) 는 무리수인가? : 귀류법 -
이걸 증명할 때 쓰이는 idea는 또 다르다.
'귀류법' 이라는걸 이용할것이다.
귀류법 : 어떤 명제가 참임을 증명할 때,
그 명제를 부정한 다음 논리를 전개하다가
모순이 발생하면, 부정이 거짓이므로
원래 명제는 참이 된다.
모순이 없다면, 부정이 참이므로 원래 명제는 거짓이 된다.
그니까 어떻게 할거냐면,
√(2)가 무리수임을 증명할건데,
귀류법을 이용해보면
√(2)가 무리수임을 부정하는건
'√(2)가 유리수' 라는거고
'√(2) 가 유리수라 가정' 하고 논리를 전개하다가
모순이 발견되면, √(2)가 유리수가 아니라는것이다.
그러면 √(2)가 무리수라는 것이 자연스럽게 증명 완료된다.
물론 이게 아주 엄밀한 증명은 아니다.
유리수가 아니면 무리수이거나 허수이기 때문에
√(2)가 실수라는것도 증명해야한다.
이건 여기서 다루기는 너무 어려우니 그냥 실수라 치고 패스했다.
귀류법 : √(2)가 유리수라고 가정한다.
√(2)가 유리수라면,
유리수의 정의에 의해
√(2)는 서로소인 두 정수의 비로 나타낼 수 있어야한다.
√(2)는 양수니까, 서로소인 두 자연수의 비로 나타낼 수 있어야한다.
즉, √(2)를 아래처럼 나타낼 수 있어야 한다.

등식의 성질을 이용한다.
양변에 p를 곱하면
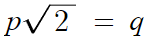
양변을 제곱하면
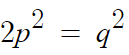
여기서, p가 자연수이므로
2p² 은 무조건 짝수인 자연수이다.
그리고 q도 자연수이므로
q를 제곱해서 짝수를 만들려면
q가 짝수여야한다.
즉, q는 짝수이다.
q가 짝수면, q는 2를 약수로 갖는다.
따라서, q²은 4를 약수로 가지며,
2p² = q² 에서 q²가 4의 배수이므로
p²은 2의 배수, 즉 짝수이다.
따라서 아까와 같은 논리로
p도 짝수이다.
그런데, p와 q가 둘다 짝수면

처음에 써놓은 식에서
p와 q가 서로소라는 가정에 모순된다.
따라서, √(2)는 유리수가 아니다.
따라서, √(2)는 무리수이다.
Q. E. D.
- 예제 -
1 )
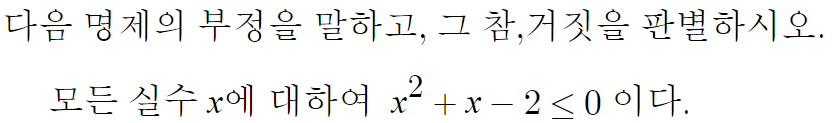
우선 주어진 명제는

이거고, 우리가 이해하기 쉽게 다시 쓰자면

따라서, 이 명제의 부정은
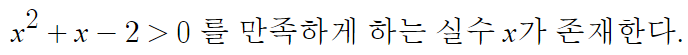
문제에서 처음에 제시한 명제처럼 형태를 갖춰서 다시 쓰면,
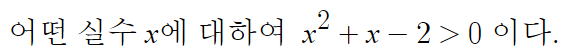
이제 이것의 참, 거짓을 판별할거다.
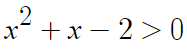
이건 이차부등식이고,
이차부등식을 푸는법은 수학(상)에서 배웠다.
풀어보면 -2<x<1 이라 나온다.
실수해가 존재하므로,
주어진 명제의 부정은 참이다.
추가로, 부정이 참이므로 주어진 명제는 거짓임을 알 수 있다.
2 )

p 조건을 절댓값 벗겨서 다시쓰면
p: -1<x<1
따라서, p가 성립하면 q도 무조건 성립한다.
즉, p→q 가 성립한다.
그리고, q가 성립한다고 p가 무조건 성립한다는 보장은 없다.
따라서, q→p 는 성립한다는 보장이 없다.
따라서, p는 q이기 위한 '충분조건' 이다.
다른 풀이 )
p, q의 진리집합을 각각 P, Q 라고 하면
Q가 P를 다 포괄하고 있으므로
P는 Q의 부분집합이다.
그리고 P≠Q 이다.
따라서 p는 q이기 위한 '충분조건' 이다.
3 )

- 첫번째 빈칸 -
결론을 q라 하면,
q: x 또는 y 는 무리수이다.
따라서 첫번째 빈칸에 들어갈 것은
'x 또는 y'
- 두번째 빈칸 -
p→q 의 대우는 ~q→~p 이다.
따라서 두번째 빈칸에 들어갈 것은
'~q→~p'
- 세번째 빈칸 -
세번째 빈칸에는
~q 를 문장으로 표현한게 들어가야한다.
~q는 q의 부정이고, q : x또는y 는 무리수이다.
이므로, ~q : x와 y는 유리수이다.
따라서 세번째 빈칸에 들어갈 것은
'x와 y가 유리수'
'수학(하) > I. 집합과 명제' 카테고리의 다른 글
| 명제 #5 - 절대부등식 (산술평균과 기하평균) (0) | 2022.05.25 |
|---|---|
| 명제 #3 - 명제 p→q, 명제의 역과 대우 (0) | 2022.05.15 |
| 명제 #2 - 조건과 진리집합, 부정 (0) | 2022.05.07 |
| 명제 #1 - 명제란 무엇인가? (0) | 2022.04.28 |
| 집합 #5 - 집합의 연산 (0) | 2022.04.15 |



