
- 개요 -
1단원의 마지막 내용이다.
어렵지는 않은데, 약간의 암기가 필요하다.
- 절대부등식이란? -

우선 이 명제의 참, 거짓을 판별해보자.
당연히 참임을 알 수 있다.
이런식으로,
항상 성립하는 부등식을 절대부등식이라 한다.
항상 성립하는 등식을 항등식이라 하는것과 비슷하다.
- 절대부등식을 왜 쓰는가? -
항등식을 처음 배울때와 비슷한 의문이 있을 수 있다.
항상 성립하는건 의미가 없지않을까?
여기서는 무슨 의미가 있냐면,

이 말은 무슨 의미냐면
a²의 '최솟값'이 0보다 크거나 같다는말이다.
즉, a²의 계산값은 아무리 작아도 0보다 작아지지는 못한다.
어떤 수식에서의 계산값이 어느 범위에 있는가?
이 수식보다 항상 계산값이 큰 수식은 무엇인가?
절대부등식이라는 이름으로 이런것들을 다룰 수 있는것이다.
- 절대부등식의 증명에 쓰이는 재료 -
절대부등식을 왜 수학(상)의 부등식 단원에서 안다루고
여기서 다루는거냐면,
이걸 수학적으로 증명해서 써야하는데
수학적 증명 이라는것 자체를 명제 단원에서 배웠기 때문이다.
그리고 그 증명의 재료를 여기서 설명해준다.
'부등식의 성질' 을 이용한다.


동치라는건 무슨말이냐면,
둘이 하나도 다른것없이 완전히 똑같다는 뜻이다.
a>b 이면, 양변에 b 빼주면 a-b>0 되는거고
그래서 둘은 완전히 똑같이 취급해도 된다.
우리가 명제단원에서 배운 용어를 쓰자면,
a>b 는 a-b>0 이기 위한 '필요충분조건' 이다.
이건 우변을 0으로 만드는 것에 의미가 있다.

실수의 제곱은 항상 0보다 크거나 같다.
너무 당연한건데 언급되는 이유는,
'실수의 제곱은 항상 0보다 크거나 같다' 라는걸
절대부등식을 증명할 때 많이 쓴다.

a²이랑 b²은 둘다 무조건 0보다 크거나 같다.
따라서, a²+b²=0 이 되려면
a²과 b²이 둘다 0인 수밖에 없고
그러려면 a=b=0 이어야한다.

당연한것이니 패스
절댓값을 다룰때, 절댓값의 제곱이면 절댓값기호 빼도되고
저렇게 절댓값기호를 나눠서 적용해도 된다.

a>0, b>0 라는 조건은 왜 들어갔냐면
b가 음수인데 a보다 절댓값은 클수도 있는거고
그러면 a²<b² 이 될것이다.
따라서, 저게 동치가 되려면 a와 b가 둘다 양수여야한다.
- 절대부등식 1 -

± 기호는 실수로넣은게 아니라
저부분의 부호가 '+'여도 성립하고 '-'여도 성립하니까 하나로 합친거다.
등호는 a=b=0 일때만 성립한다는건 그냥 말 그대로다.
a=b=0 이라는 매우 특수한 케이스에서만 0이 된다.
- 증명 -
직접 해볼수 있다면 매우 좋다.

a²-ab+b²≥0 인것도 같은방법으로 증명되니 생략
- 절대부등식 2 -

- 증명 -

- 절대부등식 3 -

- 증명 -

- 산술평균과 기하평균 -
산술평균과 기하평균의 관계는 절대부등식으로 설명되는데,
우선 산술평균이 뭐고 기하평균이 뭔지부터 알아야한다.
산술평균 : 합의 평균
우리가 일상적으로 말하는 평균이 산술평균이다.
즉 다 더한다음 개수로 나누는것
예를 들어, 2와 8의 산술평균은
(2+8)/2 = 5
기하평균 : 곱의 평균
다 곱한다음 제곱근을 취한다.
예를 들어, 2와 8의 기하평균은
√(2×8) = 4
일반적으로, 산술평균과 기하평균은 값이 다르게 나온다.
- 기하평균을 왜 쓰는가?
곱의 평균을 구하고 싶을때 쓴다.
예를 들자면, 증가율 정도가 있겠다.
어떤 물건의 초기 가격이 10만원이었는데,
1일 뒤엔 11만원, 2일 뒤엔 9.5만원, 3일 뒤엔 11.5만원이 되었다.
이 물건의 평균적인 가격 증가율은 기하평균을 이용해서 구한다.

1.047 아래의 소숫점은 반올림하여 1.048로 근사한다.
1.048 = 104.8% 이므로
매일 가격이 평균적으로 4.8%씩 올랐다고 볼 수 있다.
저런 식을 어떻게 세우는지 자세한 설명없이 그냥 했는데
몰라도 돼서 그렇다. 어차피 중요한건
다음에 나올 '산술평균과 기하평균의 관계'이다.
- 절대부등식 4 : 산술평균과 기하평균의 관계 -

이를 수식으로 나타내면,

좌변이 산술평균이고 우변이 기하평균이다.
a=b 라고 하면 등호가 성립함을 알수 있다.
증명은 간단하다.
딴건 몰라도 이정도는 증명할줄 알아야 까먹지 않는다.

Q) a나 b가 허수면 a-b가 허수가 되고 그럼 제곱하면 음수 아닌가요?
A) a>0, b>0 이라는 전제조건이 들어가있다.
허수는 음수, 양수의 개념이 없다.
크기 자체를 논할수 없는 수가 허수이기 때문이다.
쉽게 말해서, a>0, b>0 이라는 조건 자체로
a, b가 둘다 실수라는 뜻이다.
- 산술평균 ≥ 기하평균 활용 -
이건 문제에서 어떻게 활용되냐면,

뜬금없어보이지만 산술평균과 기하평균의 관계를 이용하는 문제이다.
x와 1/x 의 산술평균과 기하평균을 구한다음
x와 1/x의 산술평균은 기하평균보다 크거나 같으므로
x와 1/x 의 산술평균의 최솟값은 기하평균이다.
x와 1/x 의 산술평균은

이건데, 얘의 값이 기하평균과 똑같아지는순간이 바로
x+1/x 가 최솟값이 되는 순간이다.
x와 1/x 의 기하평균은

따라서, 산술평균과 기하평균의 관계에 의해

양변에 2를 곱해주면,

따라서, x+1/x 의 최솟값은 2 이다.
따라서 답은 2
조금 다르게 풀수도 있다.
산술평균과 기하평균이 같아지는 순간이
x+1/x 가 최소가 되는 때 라는것까진 똑같이 간다.
근데 산술평균 = 기하평균일 조건이 따로 있다.

a=b 이면 a+b가 최소가 된다.
이 문제에서는 a=x, b=1/x 였던것이다.
즉, x = 1/x 일 때, x+1/x 는 최소가 된다.
x>0 이므로, x = 1/x 를 만족하는 x값은 1밖에 없다.
따라서, x+1/x 의 최솟값은 x=1 대입하면
1+1/1 = 2
따라서 답은 2이다.
주의할 것은,
산술평균과 기하평균의 관계를 이용할거면
a와 b가 둘다 양수여야한다.
만약 a와 b중 하나가 음수가 되면
기하평균이 허수가 된다.
허수는 크기 자체를 논할수 없어서, 저 절대부등식을 이용할수 없다.
a와 b가 둘다 음수라면
좌변은 음수인데 우변은 양수라서 성립하지 않는다.
따라서, a와 b가 둘다 양수일때만
산술평균과 기하평균의 관계(절대부등식)를 이용할 수 있다.
- 절대부등식 5 : 코시 슈바르츠 부등식 -
이건 사실상 외워야하는거라 다루기 애매하다.

문제는 보통 어떻게 나오냐면,
x²+y²=5 일때 2x+3y의 최댓값은?
2x+3y=5 일때 x²+y²의 최솟값은?
이런식으로 물어본다.
공식 때려박으면 너무 쉽게 끝나버린다.
그래서 수능에는 이런 공식지향적인 문제는 거의 출제되지 않는다.
즉, 내신용 수학이다.
대신 수학적으로는 중요한 식이라서,
진로계획을 이과쪽으로 잡고있다면, 공부해서 나쁠건 없다.
증명은 교과서에 나오는 증명법과,
내 기하적인 증명법
이 2가지를 다룰것이다.
증명 1 : 교과서에 나오는 증명법

증명 2 : 기하적인 증명법

이 기하적 증명법을 이용하면,
코시 슈바르츠 부등식을 아래와 같이 확장할 수 있다.

사실 이게 진짜 일반화된 코시 슈바르츠 부등식이다.
코시 슈바르츠 부등식은 그냥 외우는게 좋다.
어차피 수능에 거의 안나오며,
내신용인데 내신은 암기 위주니까 그냥 암기하자.
- 예제 -
1 )

4x와 9/x 둘다 양수이므로
산술평균과 기하평균의 관계인 절대부등식을 이용할 수 있다.
산술평균≥기하평균
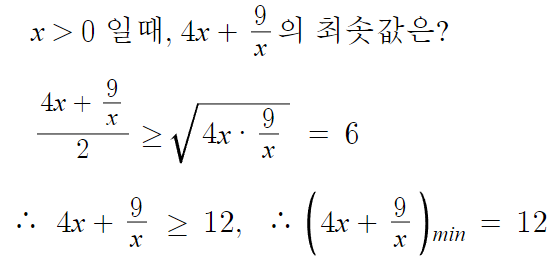
따라서 답은 12
다른 풀이
산술평균≥기하평균 이므로
4x+9/x의 값은
4x=9/x 일때가 최소이다.

따라서 답은 12
2 )

3x+4y=5 인데
3, x, 4, y는 다 실수이고
x²+y² 의 최솟값을 구하라고 하니
코시 슈바르츠 부등식을 이용해보자고 추론할 수 있다.

여기서 a=3, b=4 라고 두면 끝난다.
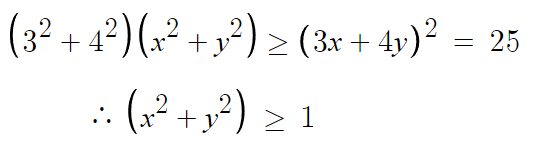
따라서 x²+y²의 최솟값은 1이고
답은 1이다.
다른 풀이 : 기하적인 풀이
이 풀이는 몰라도 된다.
코시 슈바르츠 부등식 외우기 귀찮아서
다른 풀이 연구해보다가 발견한 풀이이다.
x²+y² = r² (r>0) 이라 하면
이건 반지름의 길이가 r이고
중심이 원점인 원의 방정식이 된다.
그러고 나서, 반지름 r의 최솟값을 구하면 되는거다.
그리고 3x+4y=5 라고 한다.
이건 직선의 방정식이다.
이 직선이 x²+y² = r² 인 원을 지나야한다.
그러기 위한 r값중 가장 작은것을 구하면 되는거다.
그렇게 되려면,
원과 직선이 접하면 r이 최소가 된다.
즉, r=d 이면 된다.
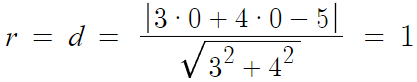
따라서 r의 최솟값은 1이며
따라서 x²+y²의 최솟값도 1이다.
따라서 답은 1
'수학(하) > I. 집합과 명제' 카테고리의 다른 글
| 명제 #4 - '모든'과 '어떤', 충분조건과 필요조건, 수학적 증명법 (0) | 2022.05.19 |
|---|---|
| 명제 #3 - 명제 p→q, 명제의 역과 대우 (0) | 2022.05.15 |
| 명제 #2 - 조건과 진리집합, 부정 (0) | 2022.05.07 |
| 명제 #1 - 명제란 무엇인가? (0) | 2022.04.28 |
| 집합 #5 - 집합의 연산 (0) | 2022.04.15 |



