
혹시 본인이 못 푼 문제인데
어떻게 푸는건지 궁금해서 이 글을 보는거라면
이 글을 보지 말것.
남이 풀어주는걸로는 실력이 늘지 않는다.
풀긴 풀었는데 풀면서 100%확신하진 못하고 약간 찜찜했거나
다른 풀이도 있을까 해서 찾아보는거라면
매우 환영이다.
원하시는 문제로 바로 가고싶으면
N번 문제로 가고싶다면
N )
이 형태로 검색하시면 됩니다.
예를들어 31번 문제로 가고싶으면 31 )
쉬운건 빠르게 넘어가면서
비약 하나도 없이 풀어보겠습니다.
제 생각에 가장 출제자의 의도에 근접했다 생각한 풀이만 담았습니다.
16 )

간단한 로그의 성질 문제

답은 6
17 )

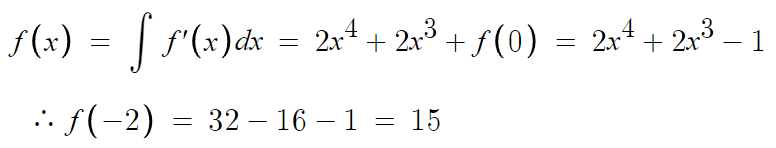
답은 15
18 )

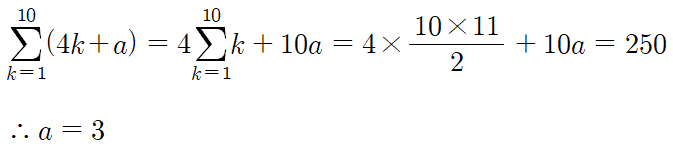
답은 3
19 )

일단 극소를 판별하기 가장 쉬운방법이 바로 미분해보는건데,
그러려면 일단 미분가능한함수인지부터 봐야한다.
f(x)는 다항함수기때문에 미분가능하다.
따라서, 극점을 미분해서 찾아도 된다.
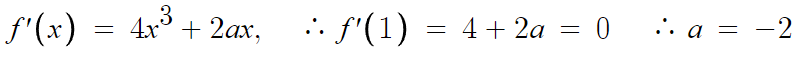
따라서 a=-2 이다.
혹시 질문있을까봐 미리 답해주자면,
도함수가 0이라고 무조건 극점인건 아니지만,
미분가능한 함수에서 극점이려면 일단은 도함수가 0이어야한다.
다음으로 극댓값이 4라니까 일단 극대지점이 어딘지부터 찾자.

따라서 f(0) = 4 , f(0) = b 이다.
따라서 b = 4 이고
a+b = -2+4 = 2
따라서 답은 2
20 )

g(x)는 정적분으로 정의된 함수인데,
적분구간에 x도 있다.
이런건 99% 미분하라는 뜻이다.
그리고 그렇게 정의된 g(x)의 극소지점을 알려준다.
극소지점을 찾는 가장 쉬운방법이 바로 미분하는거다.
f(t)에 절댓값 씌운걸 적분하는데 이게 과연 미분 가능하느냐?
미분 가능하다. 정적분은 그냥 넓이이기 때문에,
피적분함수인 이차함수에 절댓값씌우는 정도로는
미분불가능하게 되지 않는다.
이에 대해서는 이 블로그에서 언젠가 다뤄주겠다.
양변을 미분하면
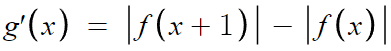
절댓값이 있는데도 그냥 이렇게 미분해도 되는 이유를 묻는다면
6모 분석할시간에 개념이나 똑바로 잡으라고 하고싶지만
그래도 설명해주자면,
|f(x)| 의 부정적분을 |F(x)| 라 하면
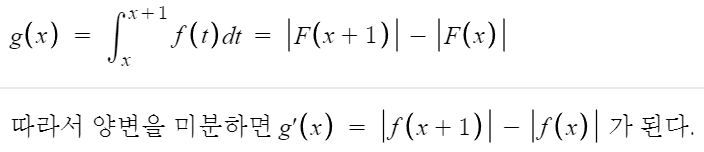
아무튼 문제로 돌아와서
양변을 미분하면
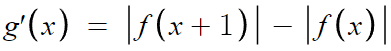
이건데, 이게 x=1과 x=4 에서 극소라고 한다.
극소이면, 일단 도함수의 값은 0이므로,
x=1과 x=4를 대입하면,
다음의 두 관계식을 얻는다.
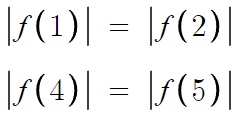
근데 f(x)는 최고차항의 계수가 2인 이차함수이다.
즉, f(x)가 아래와 같이 생겼다는거다.
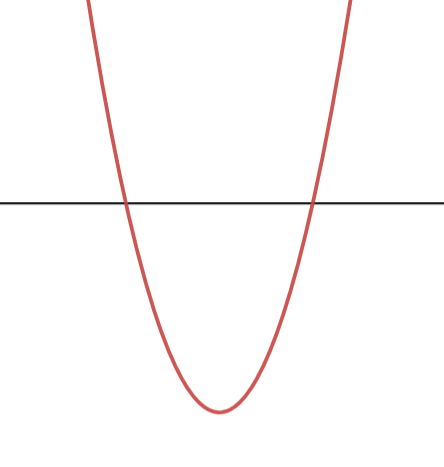
이런 이차함수에서,
x값이 다른데, 함숫값의 절댓값이 같을 수 있는 부분은
세군데 밖에 없다.
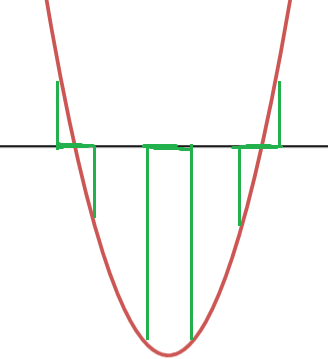
녹색으로 표시한 세 지점이다.
그럼 저중 하나는 x=1, x=2 이고
하나는 x=4, x=5 라는건데
나머지 하나는 뭔가?
이 질문의 답은 문제에서 쓴 문장에 있다.
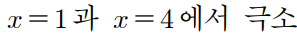
x=1과 x=4 에서 극값도 아니고 극소?
'극소'지점 두개를 가지려면
극소 극대 극소 번갈아가면서 나와야하므로
극대지점이 무조건 나와줘야한다.
그럼 결론은 나왔다.
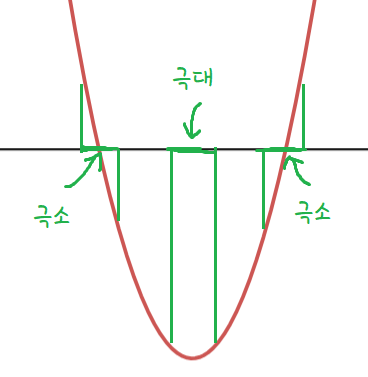
따라서, x=1, x=2, x=4, x=5 가 어디인지 표시할 수 있다.
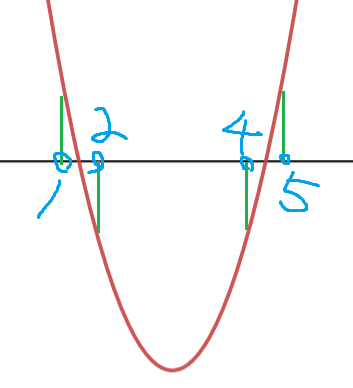
따라서, f(1) = -f(2) 이며
f(4) = -f(5) 이다.
따라서, f(1) + f(2) = f(4) + f(5) = 0 이며
2로 나눠주면
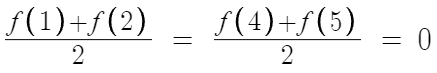
둘다 평균값이 0이므로,
결론적으로 이차함수 f(x)는
x=3을 기준으로 대칭이다.
따라서, f(x)의 꼭짓점은 x=3 이다.
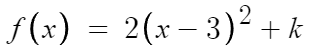
k값만 구하면 끝난다.
f(1) = -f(2) 라는걸 이용하면 될것이다.
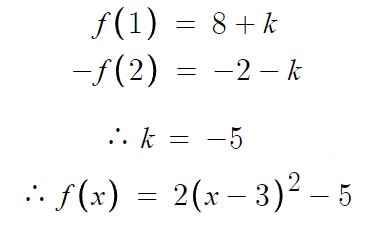
이제 f(0)을 구하기 위해
x=0 만 대입하면 끝
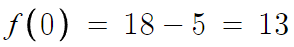
따라서 답은 13
21 )
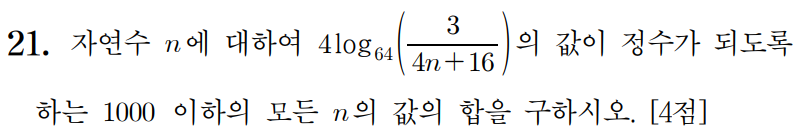
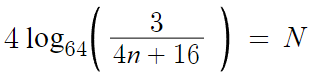
저것의 값을 N이라 놓겠다.
N은 정수이다.
로그를 벗겨서 정리하면 이렇게된다.
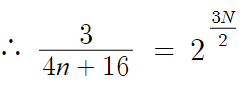
따라서, 아래와 같은 결론을 얻는다.


따라서, 4n+16 을 이렇게 쓸 수 있다.
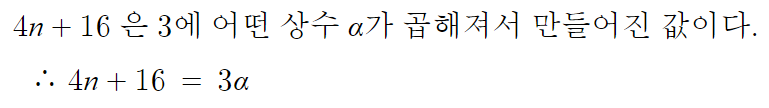
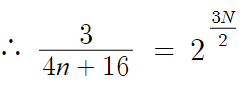
여기에 대입해주면,
α 에 대한 조건을 찾을 수 있다.
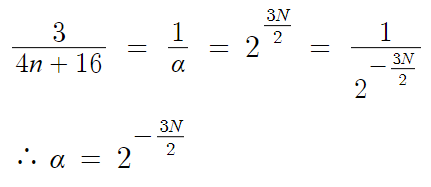
N이 정수이니, N의 값을 하나씩 넣어보면 규칙을 찾을 수 있다.
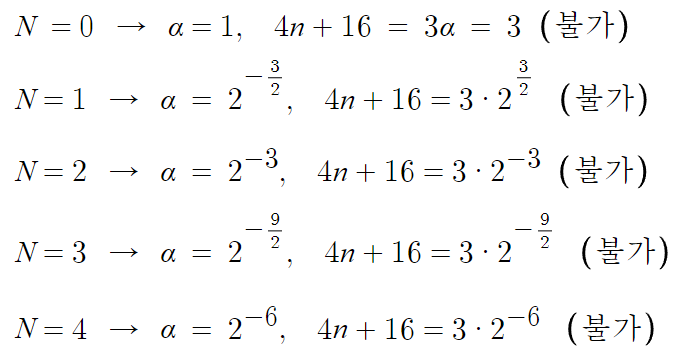
일단 해보면 알겠지만, N은 음수여야한다.
N이 양수면, 자연수 n을 가지고 저런 값을 만들수 없다.
N이 커질수록 α값은 작아지기 때문에,
양수인 N에 대해서는 더이상 해볼 필요가 없다.
따라서, N이 음수임을 감안하여 이번엔 N=-1 부터 또 넣어볼거다.

이것도 해보면 알겠지만, N은 짝수여야한다.
N이 홀수면, 2의 1/2 제곱근이 등장하는데,
자연수 n을 가지고 그런 값을 만들 수 없다.
참고로, -2, -4, -6 전부 짝수이다. 2로 나누어떨어지면 짝수이다.
모르는사람이 많은거같다.
그럼 이번엔 N이 짝수인것까지 감안하여 넣어보면
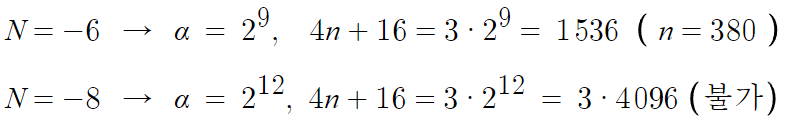
N=-10 같은것도 이제 안해봐도 된다.
α값이 너무 커져서, n이 1000을 넘어가버릴것이다.
따라서, 가능한 n은
n=2, n=44, n=380 이고
셋을 더하면, 2+44+380 = 426
따라서 답은 426
22 )

개인적으로 쉽게 풀었는데, 정답률을 보니 쉬운문제는 아니었나보다.
아마 식의 생김새가 무시무시하게 생겨서 겁먹은게 아닐까?
우선, 문제를 읽어보니 g(x)가 연속이란다.
근데 g(x)는 범위를 두개로 나눠서 정의된 함수이다.
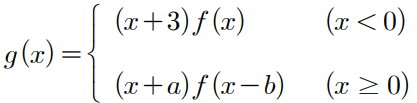
f(x)는 이차함수이기 때문에
g(x)는 삼차식이 될것이다.
삼차식은 연속함수이므로,
경계지점인 x=0 에서 연속이라면,
g(x)는 연속이다.
연속임을 검사하는 방법은
좌극한 = 우극한 = 함숫값
좌극한은 3f(0) 이고 우극한(함숫값)은 af(-b) 이므로
둘을 같다고 놓으면 된다.
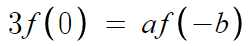
근데 여기서 더 파볼수는 없다.
f(x)가 이차함수라는것 외에 a나 b의 정보가 빈약하기때문이다.
따라서, 이젠 아래의 조건을 써봐야한다.
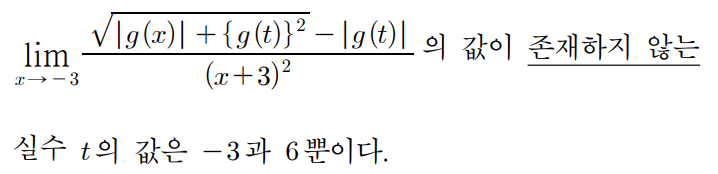
저 식의 극한값이 존재하지 않는 실수 t의 값은 -3과 6 뿐이다.
이는 다시말하면, t=-3과 t=6 을 제외하면 전부 극한값이 존재한다는것이다.
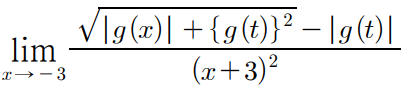
일단 이것의 극한값을 다뤄야하는데,
여기서는 식조작의 발상이 필요하다.
난 이렇게 생각했다.
1. 분자에 루트와 절댓값이 있으며, 식이 너무 더럽다.
2. 루트 안에 플러스 제곱이 들어있고, 루트 밖엔 마이너스 절댓값이 있다.
3. 따라서, 합차공식을 이용하면 루트도 벗겨내고
식도 간단히 할 수 있을것같다.
한번 해보자.
더러운 식이 한번에 몰아치니 마음의 준비를 조금 하자.
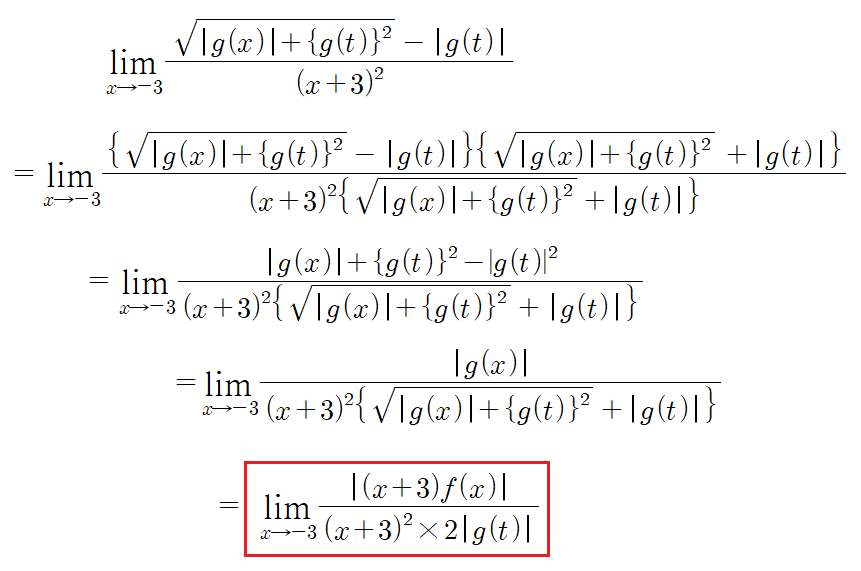
식을 간단하게 만드는데 성공했다.
여기서 중요한 질문이 있을수 있는데,
분모의 |g(x)| 에 대한 질문이다.
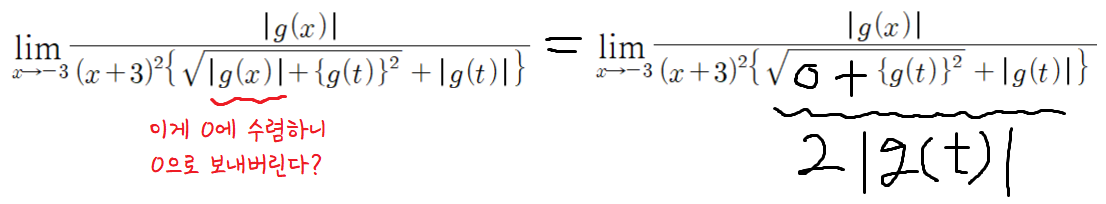
|g(x)| 가 x=-3 에서 0에 수렴하는거지,
그 값 자체가 0인건 아니기때문에
|g(t)| = 0 인 경우도 생각하기 위해서는
|g(x)|도 남겨놔야하는데,
분모의 |g(x)|를 누구맘대로 없애버리냐? 이거다.
그 말이 맞다.
그게 이 문제의 핵심이다.
그래서 사실은 이런 조건이 있어야한다.
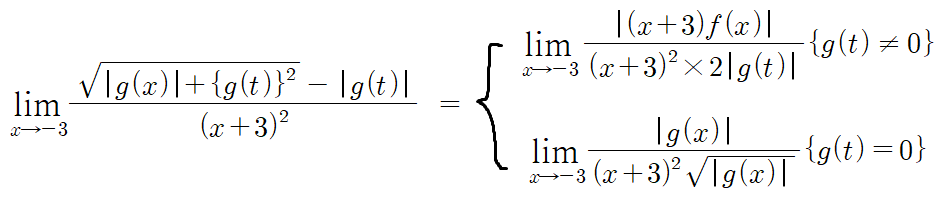
근데 g(t)=0 일때를 잘 보자.
g(t)=0 이면 극한값이 절대로 존재할수가 없다.
g(x)는 삼차식이기 때문에,
분자는 최종적으로,
삼차식에 절댓값과 루트 씌운것이 될것이다.
따라서 g(t)=0 이면 저 극한식은 무한대로 '발산'하게 된다.
그래서 아까 식 정리할때
|g(x)| 를 그냥 0으로 보내버리고 정리한것이다.
해설강의나 해설지에 이 과정이 언급이 안돼있는 경우가 많은데,
너무 불친절하다 생각한다.
그렇게 비약적으로 푸니까 학생들이 이해를 못해서
킬러는 내가 풀게 못되는구나 하면서
킬러를 손도못대게 되는거다.
아무튼 문제로 돌아와서,
구한 극한 식은 아래와 같다.

일단 g(t)는 아까 구했듯 0이 아니므로
적당히 떼어내면, 이렇게 된다.
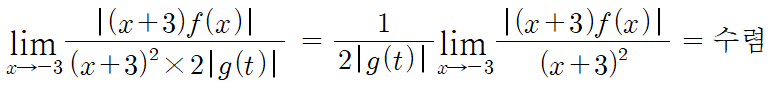
따라서, 저게 수렴하려면
분자도 (x+3)² 을 인수로 가져야하므로
f(x)는 x+3 을 인수로 갖는다.
따라서 f(x)는 이렇게 쓸 수 있다.
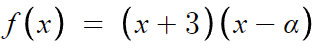
이걸 대입해서 아까 극한 식에 다시 쓰면,
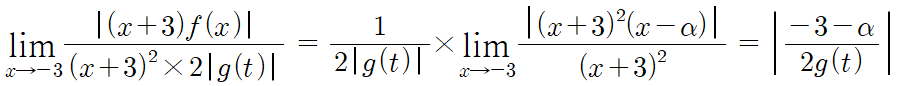
따라서, 주어진 극한 식은 |-3-α| / 2|g(t)| 에 수렴한다.
근데 좀 이상하지 않은가?
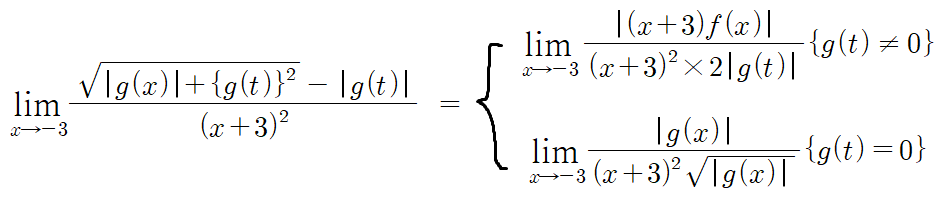
우리는 방금 g(t)=0 일땐 무조건 발산하니까
g(t)≠0 일때 수렴할 조건을 다룬건데,
진짜 g(t)≠0 이기만하면 무조건 수렴해야하는것 아닌가?
그래서, 극한값이 존재하지 않을 방법이 바로
g(t)=0 인 수밖에 없는 것이다.
따라서, 아래와 같은 결론을 얻는다.
주어진 극한식이 수렴하지 않으려면,
무조건 g(t)=0 이어야한다.
문제에선 t = -3, t = 6 에서 수렴하지 않는댔으니
g(-3) = g(6) = 0 이다.
그리고, t = -3, t =6 '에서만' 수렴하지 않는댔으니
g(t)=0의 실근은 t=-3, t=6 만 나와야한다.
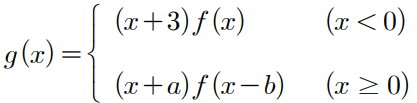
아까 구한 f(x)를 여기다 대입하면,
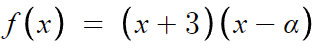
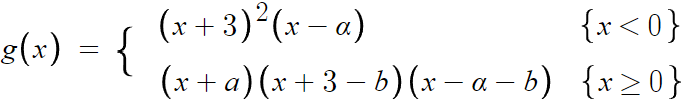
이것의 실근이 x=-3, x=6 뿐이다.
따라서, α는 음수면 안된다.
음수가 되고싶다면 α = -3 이어야한다.
그렇지 않으면, g(x)의 실근이
x<0 범위에서 -3 이외의 다른것도 등장하게 되고,
그럼 문제의 조건에 맞지 않는다.
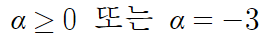
다음으로, x≥0 일때도 보면,
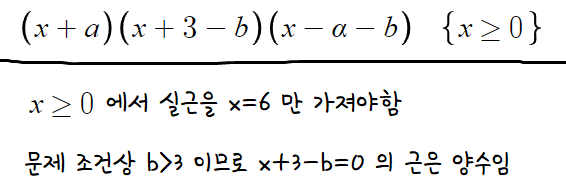
따라서, 다음과 같은 결론을 얻는다.

따라서, 종합하면 이렇게된다.
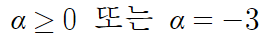

이걸 둘다 만족하려면,
α=-3 이며, b=9 인 수 밖에 없다.
따라서, f(x)의 추론이 끝났다.
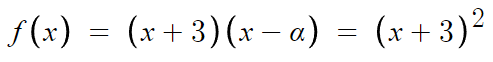
이걸 이용해 g(x)도 다시 작성하면,
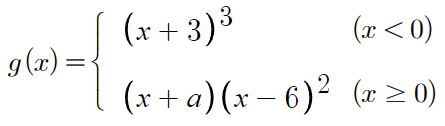
우리는 이제 모르는 미지수가 a밖에 없다.
a값은 쉽게 구할 수 있다.
우리가 처음에 작성해놓고 아직 한번도 안쓴 관계식이 있다.
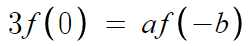
대입해주면,
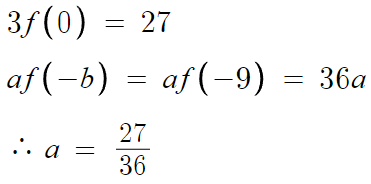
이제 진짜 다했다.
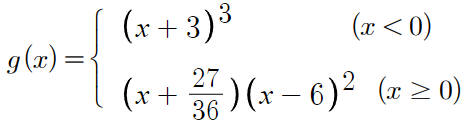
g(4)를 구하라니까,
x=4 를 대입만 해주면 끝난다.

따라서 답은 19
'2023학년도 기출 해설 > 2023학년도 6월 모의평가 해설' 카테고리의 다른 글
| 2023학년도 6월 모의평가 물리II 해설 (0) | 2022.06.25 |
|---|---|
| 2023학년도 6월 모의평가 물리I 해설 (0) | 2022.06.22 |
| 2023학년도 6월 모의평가 수학 확률과통계 23번~30번 해설 (0) | 2022.06.18 |
| 2023학년도 6월 모의평가 수학 미적분 23번~30번 해설 (0) | 2022.06.12 |
| 2023학년도 6월 모의평가 수학 공통 1번~15번 해설 (0) | 2022.06.10 |



