
혹시 본인이 못 푼 문제인데
어떻게 푸는건지 궁금해서 이 글을 보는거라면
이 글을 보지 말것.
남이 풀어주는걸로는 실력이 늘지 않는다.
풀긴 풀었는데 풀면서 100%확신하진 못하고 약간 찜찜했거나
다른 풀이도 있을까 해서 찾아보는거라면
매우 환영이다.
원하시는 문제로 바로 가고싶으면
N번 문제로 가고싶다면
N )
이 형태로 검색하시면 됩니다.
예를들어 17번 문제로 가고싶으면 17 )
쉬운건 빠르게 넘어가면서
비약 하나도 없이 풀어보겠습니다.
제 생각에 가장 출제자의 의도에 근접했다 생각한 풀이만 담았습니다.
이것저것 설명하려다보니, 글에 사진이 너무 많아졌습니다.
사진이 불러와지지 않거나, 버벅거리는 버그가 있을수도 있습니다.
23 )

기본문제니까 자세한 설명은 생략

답은 1번
24 )

기울기가 바로 dy/dx 인데
쓰기 귀찮으니, dy/dx = m 이라 두고 풀겠다.

양변을 미분하면

( e, e² ) 를 대입하면

따라서 답은 1번
25 )

역함수의 미분문제

따라서 답은 2번
26 )
문제가 너무 길어서 두장으로 나눠올립니다.


일단 일정한 비율로 축소되면서 만들어내는 도형들이니
새로 만들어지는 도형의 넓이는 일정한 비율로 감소할것이다.
따라서 새로 만들어지는 도형의 넓이는 등비수열이다.
따라서, 등비수열의 무한합 공식을 이용한다.

일단 첫번째 항을 구하고
그다음 공비까지 구해서 계산하겠다.
- 첫번째 항(a) 구하기 -
문제에서 준 조건들만 표시하면

근데 여기서, 문제에서 준 다른 힌트들을 이용하면
정삼각형을 찾을 수 있다.


따라서, 아래와 같은 결론을 얻는다.


따라서, 또 아래와 같은 결론을 얻는다.
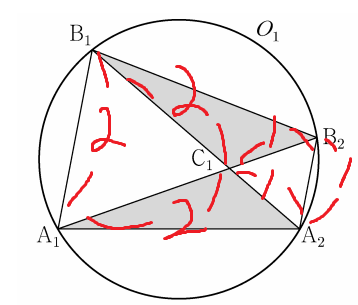
길이들을 표시한것이다.
이젠 넓이를 구할 수 있다.
A₁B₁B₂A₂ 의 넓이를 구한다음,
아까 찾아낸 두 정삼각형의 넓이를 빼주면 된다.
A₁B₁B₂A₂ 는 윗변과 아랫변이 평행한 사다리꼴이므로,
A₁B₁B₂A₂ 의 넓이는

이제 두 정삼각형의 넓이를 빼주자.

따라서, 우리가 구하고자하는 넓이는

- 공비 구하기 -
우리가 첫째항을 구하면서 길이를 표시하는 과정에서
이미 알게 되어있다.
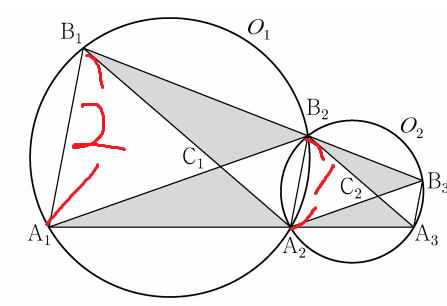
원래 길이가 2였는데,
새로 만들어진 도형에선 1이 되었다.
따라서, 길이의 공비는 1/2 이다.
따라서, 넓이의 공비는
길이의 공비의 제곱인 1/4 이다.
r = 1/4
- 대입하면 끝 -


따라서 답은 2번
27 )

급수가 수렴하려면, 더해지는것 자체가 0에 수렴해야한다.
수식으로 쓰면, 아래와 같다.

따라서, a_n / n 의 수렴값을 알아낼 수 있다.

그런데, a_n 은 등차수열이므로,
a_n은 일차식이다.
따라서, a_n을 이렇게 쓸 수 있다.

-3은 왜 나왔냐면,
n=1 을 대입했을때 a₁, 즉 4가 나와야하기 때문이다.
따라서, a_n 은 공차가 3인 등차수열이다.
이걸 대입해서 수렴값 S만 구하면 끝이다.


따라서 답은 3번
28 )

28번치고는 꽤 어렵지않았나 싶다.
29번도 쉽지 않았다.
내 개인적인 생각을 좀 덧붙이자면,
이번 시험은 미적분 난이도조절에 실패했다.
- (가) 조건 풀이 -

무슨말이냐면, x가 1만 아니면 g(x)는 무조건 연속이다.
x=1 에서 불연속인지는 모른다.
아무튼 x가 1만 아니면 g(x)는 연속이다.
근데, g(x)의 정의가 이렇게 된다.

f(x)가 삼차함수, 즉 연속함수이므로
ln|f(x)| 도 연속함수이다.
물론 로그함수니 정의역은 f(x)≠0 이다.
따라서, g(x)의 연속성을 판별할때는
f(x)가 0일때와 아닐때의 그 경계지점을 보면 된다.
f(x)=0 이 되는 순간의 연속성을 보겠다는것이다.
연속이려면 극한값과 함숫값이 같아야하는데,
극한값은 ln|f(x)| 이고
함숫값은 1 이므로
ln|f(x)| = 1 이어야 하고,
따라서 g(x)가 연속이려면
f(x) = 0 일때 |f(x)| = e 이어야한다.
이게 말이 되나? 말이 안된다.
그래서, 이런 결론을 얻는다.

근데, f(x)는 삼차함수기 때문에
f(x)=0 을 만족하는 실수 x가 최소한 하나는 존재한다.
그러므로,

이 조건을 만족하려면,
f(x)=0 을 만족하는 실근 x는
유일하게 x=1 로 하나만 나와야한다.
따라서, 이런 결론을 얻는다.

물론, 중근일수도 있다. 이것만 가지고는 모른다.
그래서 이젠 (나) 조건으로 넘어가야한다.
- (나) 조건 풀이 -

극대를 다루는 가장 쉬운 방법이 바로 미분해보는것이다.
근데, 미분하기 전에 당연히 미분가능성부터 보아야한다.
미분가능성 안보고 그냥 미분해서 풀면 비약이다.
미분가능성 무시하고 풀다가 큰코다치는 수가 있다.

(가) 조건을 풀때, f(x)=0 의 실근은 x=1 밖에 없다했다.
따라서 f(x)는 x=2에서 0이 아니기때문에,
ln| f(x) | 의 x=2 에서의 미분가능성만 보면 된다.
f(x)는 그냥 삼차함수고 f(2)≠0 이기 때문에 ,
f(x)는 x=2 에서 미분가능하다.
따라서 ln| f(x) | 도 x=2 에서 미분가능하다.
왜냐면, ln의 미분이 이렇게 정의되기 때문이다.

그래서 f(x)만 미분가능하면 ln|f(x)| 도 미분가능한것이다.
x=2 에서 미분가능한 함수 g(x)가
x=2 에서 극값을 가진다는건,
g'(2) = 0 이라는 뜻이다.
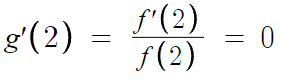
따라서, 이런 결론을 얻는다.

그런데, (나) 조건에 이런 말이 있다.

g'(2)=0 이라 극값을 가지는건 맞는데,
g(2)는 극대가 되고,
절댓값을 씌운 |g(2)| 는 극소가 된다.
그렇다는건, g(x)가 x=2 부근에서 이렇게 생겼다는거다.

g(2)는 양수가 아니며, 이 부근에서 위로 볼록하다.
( g(2)=0 일수도 있기때문에 양수가 아니라고 적은것이다 )
그래야 g(2)가 극대이면서
|g(2)|는 극소가 될 수 있다.
그런데, g(x)의 정의가 이렇게된다.

g(2) ≤ 0 이려면,
|f(2)| ≤ 1 이어야한다.
근데 f(x)는 최고차항의 계수가 양수인 삼차함수이고
유일한 실근 x=1 을 가지게 되므로,
f(x)의 그래프는 이렇게 그려질것이다.

f(x)가 y=1 과 접하는지, 접하지 않는지는 아직 모른다.
(다) 조건을 풀다보면 나온다.
그래서 이제 (다) 조건으로 넘어가야한다.
추가로, x=1 에서 중근을 가질 수 없다는것도 여기서 알아냈다.
f(x)의 그래프로 가능한건 저것밖에 없다.
우리가 따질것은, y=1에서 접하는지, 접하지 않는지
그것 뿐이다.
- (다) 조건 풀이 -

g(x)의 정의를 보자.

g(x) = 0 이려면,
|f(x)| = 1 인 수밖에 없다.
근데 아까 f(x)의 개형을 (나) 조건 풀면서 그려놨다.

우리는 |f(x)| = 1 인걸 봐야하니까
|f(x)| 의 그래프를 그릴거다.
x<1 인 지점은 y축 위로 접어올리면 된다.

근데, 저건 y=1 과 두번 만난다.
실근이 두개라는것이다.
이러면 (다) 조건과 맞지 않다.
따라서, 이런 결론을 얻는다.

그럼 이제 |f(x)| 의 개형을 제대로 그릴 수 있다.

그리고, 이를 토대로 f(x)도 어느정도 작성할 수 있다.

이제 α 값만 구하면 f(x)의 추론이 완료되는데,
이를 알아내는 재료가 있다.

(가) 조건에서 알아낸것이다.
따라서 x=1 대입해서 0 되도록 하면 된다.

α 값을 구했고, 최종적으로 f(x)의 추론이 완료되었다.
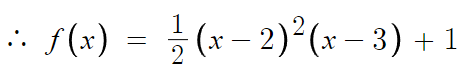
g(x)가 f(x)를 이용해서 정의되는데,
f(x)를 알아냈으므로 이제 마무리 계산만 하면 된다.
- 마무리 -

극소지점을 찾으려면, 미분해서 찾는게 쉬운데
미분가능성을 먼저 봐야한다.

근데 그건 (가)를 풀면서 이미 알았다.
x=1 을 제외하면 모두 미분가능하다.
따라서, 극소지점은
x=1 이 되거나,
아니면 미분해서 0이 되는 지점중에서
x=2가 아닌 지점
이 될것이다.
근데, x=1 은 극소지점이 될 수 없다.
g(1)=1 인데,
g(x)의 x=1 에서의 극한값은
마이너스 무한대로 발산하기때문에
g(x)는 x=1 에서 극솟값을 갖지 못한다.
추가로, 불연속이라고 극값 없다고하면 그건 비약이다.
불연속이어도 극값이 있을 수 있다.
다만 여기선 극한값 자체가 마이너스 무한대로 발산해버리므로,
g(1)은 극댓값이 되는거지, 극솟값이 되는건 아니다.
아무튼, x=2 가 아닌 지점중 g'(x)=0 을 만족하는 x값을 찾으면
거기가 바로 g(x)의 극소지점이고, 극솟값만 계산하면 된다.

g'(x)=0 이려면 f'(x)=0 이어야 한다.
즉, x=2 제외하고 f'(x)=0 인 곳이 바로 극소지점이다.
자꾸 x=2 는 왜 제외하냐면, x=2는 극대지점이다.

따라서 f'(x)=0 인 x값을 찾기 위해 f(x)를 미분할것이다.
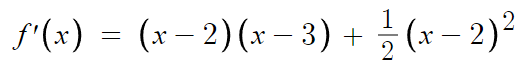
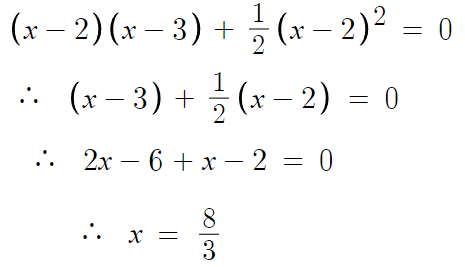
따라서 g(x)는 x=8/3 에서 극솟값을 갖는다.
즉, g(x)의 극솟값은 g(8/3) 이다.
대입만 하면 끝

따라서 답은 5번
29 )

개인적으로 22번보다 어려웠던 문제
요새 평가원이 이런 도형문제에 힘을 많이 싣고 있어서,
수험생이라면 도형문제를 많이 연습해야할것이다.
우선 문제에서 준것만 표시하겠다.

문제에서 준것만 표시했는데,
벌써 이등변삼각형이 보인다.
OAP는 이등변삼각형이다.
이등변삼각형을 왜 찾았냐면,
이등변삼각형의 성질중에 이런게 있다.
길이가 같은 두 변의 교점에서
맞은편의 변에다가 수선을 내리면,
그 선은 수직이등분선이 된다.
그림으로 보여주는게 빠르겠다.

파란선이 바로 수직이등분선이다.
정확히는 선분 AP의 수직이등분선이다.
증명은 글로만 간단히 적어주겠다.
1. 이등변삼각형은 수선에 의해 두개의 직각삼각형으로 쪼개진다.
2. 그 두개의 직각삼각형에서 수선은 공통인 변이 된다.
3. 그리고 빗변의 길이가 1로 같다.
따라서, 수선에 의해 나뉘는 두 직각삼각형은 RHS 합동이다.
따라서, 수선에 의해 나뉘는 두 직각삼각형의 밑변의 길이가 같다.
따라서, 저건 수직이등분선이다.
조금 딴길로 샜는데, 다시 돌아와서 문제를 풀어보자.
삼각형 APH를 보면,
이렇게 나뉜 두 삼각형에서 각도가 보인다.

이걸 이용하면 선분 AP의 길이를 구할 수 있다.
그러면 f(θ)를 구할때
삼각형의 높이가 되는 선분 AH의 길이도 구할 수 있는거다.

따라서, AP의 길이는 2sinθ 이고,
AH의 길이도 구하면

AH의 길이는 2sin²θ 이다.
이제 HQ의 길이만 구하면 f(θ) 를 구할 수 있다.
HQ의 길이는, 각의 이등분선의 성질을 이용하면 구할 수 있다.

증명은 여기다 적기 조금 기니 생략한다.

근데 우린 AH, AP, PH의 길이를 모두 알고있다.
따라서, 위에서 언급했던 각의 이등분선의 성질을 이용하면
HQ의 길이를 구할 수 있다.

여기서 x값은, 구하려면 구할순 있는데,
이런 문제를 푸는 팁이 있다.

문제에서 물어보는건 f(θ)와 g(θ)의 '비율'이다.
따라서, x는 식이 더러워지니 일단 남겨놓고
g(θ)를 x에 대해 나타낸 뒤 x를 약분해버리면
계산을 간단하게 만들 수 있다.
물론, 간단해지지 않으면 그냥 x 구해서 풀면된다.
이렇게 구해진 길이로 f(θ)를 구하면,

이제 g(θ) 를 구할 차례이다.

삼각형 OPS의 넓이만 구하면 된다.
왜냐면, 각의 이등분선의 성질에 의하면
AO : AP = OR : RP 이기 때문이다.
OPS의 넓이만 구하면,
비례관계를 이용해 g(θ)를 구할 수 있다.
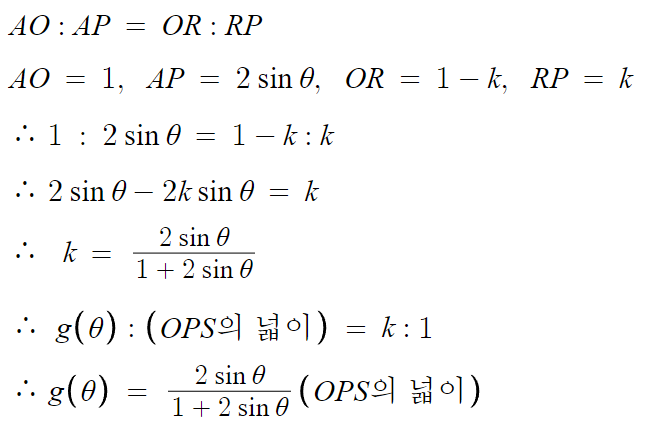
식의 가독성과 계산의 편의성을 위해, RP의 길이를 임시로 k라 뒀다.
여기서 각 ∠POS 를 α 라 둘것이다.
(α = π/2 - 2θ 이긴 하지만, 이건 좀 이따가 쓸것이다.)
(어차피 θ로 표현된다는걸 아니까 나중에 하겠다는것이다.)
그러면, 넓이를 구하기 위해 OS의 길이가 알고싶을텐데,
OS의 길이는 어떻게 구하느냐?
삼각형의 닮음을 이용한다.
삼각형 AHQ와 삼각형 AOS는 닮음이다.
따라서, 닮음비를 쓰면 OS의 길이를 나타낼 수 있다.


이젠 삼각형 OPS의 넓이를 구할 수 있다.

이젠 g(θ)도 구할수 있다.

이제 눈엣가시인 α를 θ로 나타내주기만 하면 된다.

각 AOB는 직각이고,
각 AOP는 2θ 이므로,

우리가 원하는건 sinα 이다.

이제 이걸 대입해서 g(θ) 를 다시 쓸수 있다.
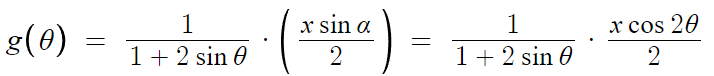
이제 마무리만 하면 된다.


x가 깔끔하게 약분되었다.
두 함수의 비율을 묻는거기 때문에,
좀 짜증나게 더러운 값을 적당히 치환해서
이렇게 약분시킬수도 있는것이다.
이제 극한값만 구하면 진짜 끝

따라서 k = 1/2 이고,
100k = 50 이다.
따라서 답은 50
30 )

난 이 문제를 보자마자 어떻게 생각했냐면,

1. 우변이 f(x)의 (t, f(t)) 에서의 접선이다.
즉 f(x)와 f(x)의 접선의 교점을 다뤄야한다.
따라서 이걸 쉽게 풀려면,
f(x)를 그래프로 그려서 직관적으로 분석하는게 쉬워보인다.

2. 그리고 f(x)가 그리기도 쉽게 주어졌다.
그럼 f(x)를 그리면 된다.
물론 적당히 개형 정도만 그리면 된다.
적당한 특징만 잡아서 개형을 그린다음,
디테일한건 문제의 조건에 맞게 조정해주면 되는것이다.
일단 f(x)는 분모가 지수함수고 분자가 다항함수이므로
f(x)는 미분가능한 함수이다.
초월함수의 그래프를 그리는 꿀팁은
x를 마이너스 무한대로 보냈을때 f(x)의 극한값
즉 x가 매우 작을때의 함숫값
x를 무한대로 보냈을때 f(x)의 극한값
즉 x가 매우 클때의 함숫값
y절편
x절편
기울기가 0이 되는 지점
변곡점
이정도를 찾은다음
미분가능하니까 부드럽게 이어주면 된다.
저게 공식은 아니고, 그냥 구하기 쉬운 특징적인 점들을
여러개 찍은다음 부드럽게 이으라는 뜻이다.
일단 x를 마이너스 무한대로 보냈을때의 극한값은

따라서 x가 매우 작아지면, f(x)는 끝없이 올라갈것이다.
다음으로 x를 무한대로 보냈을때의 극한값은

0이다.
그리고 정확히 말하면, 함숫값은 0보단 클것이다.
분모도 양수고 분자도 양수이기 때문이다.
다음으로 y절편
그냥 x=0 넣어보면 된다.

다음으로 x절편
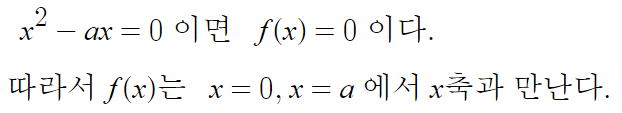
다음으로 기울기가 0되는곳, 즉 도함수가 0인곳

구하긴 했는데, 너무 더럽다.
그래서 이건 쓰지 않을것이다.
그래도 알아갈 좋은 정보는 있다.
a²+4 > 0 이므로, 실근은 두개 있다.
즉, 기울기가 0이 되는 지점은 2개 있다.
그리고, a가 양수이므로 두 지점 다 양수이다.
다음으로 변곡점

이것도 너무 더럽다.
아무튼 변곡점도 2개 있다.
그리고, a가 양수이므로 두 지점 다 양수이다.
이를 모두 종합하여 그래프를 그려보자.




x>0 에서 기울기가 0되는지점 2개, 변곡점도 2개
일단 첫번째, f(x)가 (0, 0)을 지나며,
x<0 에서는 기울기 0되는곳 없이
x가 작아질수록 무한히 커진다.
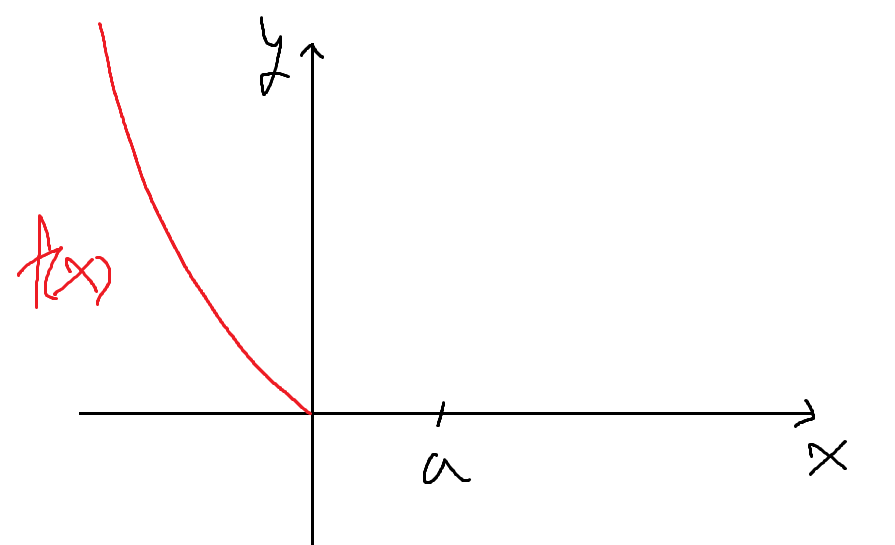
두번째, x=a 에서 x축을 지나며,
f(x)는 x=0 에서 아직 감소중이므로
x=0과 x=a 사이에서는 f(x)값이 음수일것.
그럼 적당히 중간에 기울기가 0되는지점도 있을거고
그렇게 적당히 그려주면 된다.

세번째, 기울기가 0되는 지점이 아직 하나 더 있으며,
변곡점도 어딘가에 그려진다.
그 후 f(x)는 0에 수렴한다.
정확히는 f(x)→0+ 이다.

이게 바로 f(x)의 개형이다.

이젠 쉽다. f(x)와, f(x)의 x=t 에서의 접선이
몇 번 만나는지만 보면 된다.
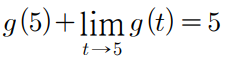
g(t)의 t=5 에서의 함숫값과 극한값을 더한게 5라고 한다.
근데 t=5라고 값을 특정지어준다고?
x=5에서의 접선이 뭔가 특별한 것이 있나보다.
즉, f(x)는 x=5에서 뭔가 event 가 일어난다.
라고 추론해 볼 수 있다.
물론 이렇게 했는데 안되면 어쩔수없이
g(t)의 그래프를 그린다음 t=5 에서의 상황을 봐야할것이다.
수능 수학문제는, 문제를 아름답게 내야하기 때문에
무조건 '특별한'지점을 물어볼 수 밖에 없다.
특징이 없는곳은 정보가 부족해서 물어볼수 없다.
이것도 문제풀이에 있어서 엄청난 꿀팁이니 알아두자.
물론 항상 그런건 아니니, g(t) 자체를 그리는 풀이도 염두해두자.
아무튼 결론은 f(x)가 x=5 에서 뭔가 특별하다는거다.
특별한 지점? 그런건 몇개 되지 않는다.
1. 기울기가 0인곳
2. 변곡점
3. 그 외 x절편, y절편 등의 다른 지점
일단 기울기가 0인곳부터 보자.
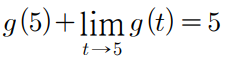
기울기가 0인곳에서 저게 만족하는지 볼것이다.

기울기가 처음으로 0이 되는 지점이 x=5 인가?
일단 저기서 g(t) = 1 이다.
그다음 극한값은,
저 기울기가 0되는지점의 바로 양옆에서
접선을 그려준다음, 교점의 개수를 찾으면 될것이다.

극한값 자체가 없기때문에, 저 지점은 5가 아니다.
근데 기울기가 0인곳이 하나 더있다. 거기도 해보자.

일단 이때 g(5) = 2 이다.
다음으로, 극한값을 보면

우극한은 3이지만 아쉽게도 좌극한이 2라서
극한값 자체가 존재하지 않는다.
따라서, 저 지점은 5가 아니다.
우리는 방금 기울기가 0인 두 지점을 해봤는데,
둘다 안됐다.
남은건 변곡점과 기타등등
변곡점을 해보겠다.
일단, 첫번째 변곡점부터 함숫값을 보면
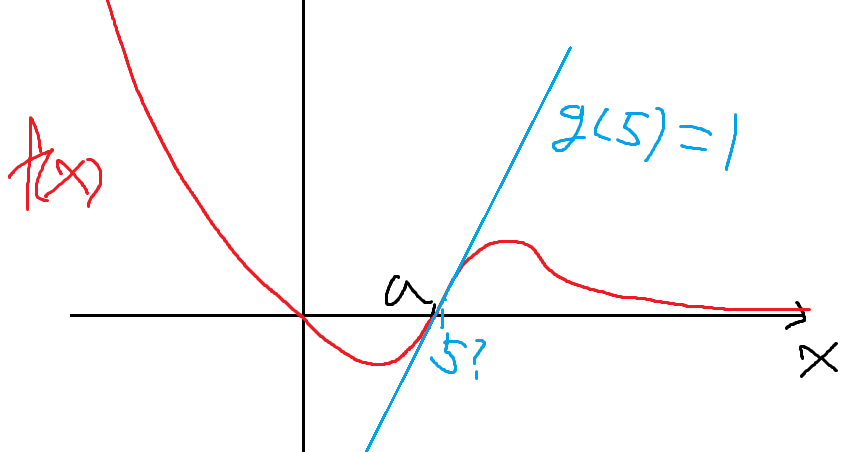
다음으로, 극한값을 보면

극한값은 2로 존재하지만,
함숫값 + 극한값 = 3 이기때문에,
조건을 만족하지 못한다.
따라서, 저 지점은 5가 아니다.
변곡점 하나 남았다. 거기도 해보자.
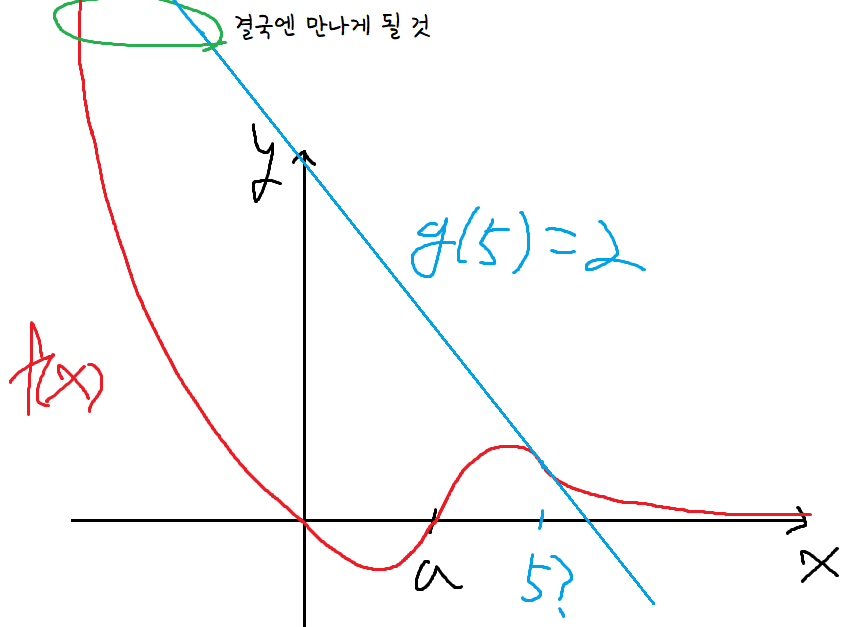
그래프를 대충그려서 좀 거시기한데,
아무튼 x가 작아진다면 결국엔 만나게 될것이다.
접선은 직선이고, f(x)는 분모가 지수함수기 때문에
f(x)가 증가하는 속도가 더 빠르다.
따라서 이때 g(5) = 2 이다.
g(t)의 t=5 에서의 극한값이 3이면 되는거다.

찾았다. 두번째 변곡점이 바로 x=5 이다.
따라서 f(x)의 개형은 이렇게 된다.

x=5 에서 f(x)가 변곡점이라는건,
f''(5) = 0 이라는것
아까 변곡점 찾느라 구해놨던 이계도함수에 대입하자.
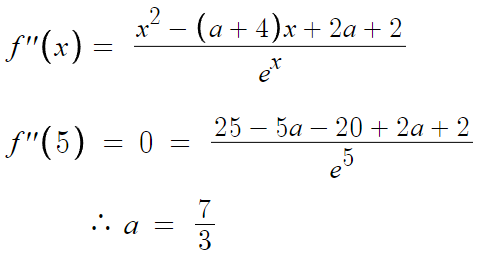
a값 구했으니 이것까지 감안해서 f(x)를 다시 그리면
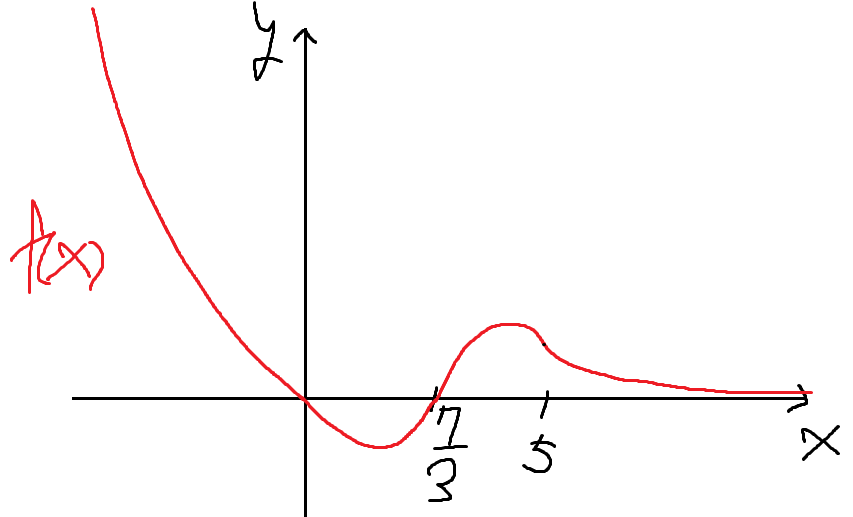
됐고, 이제

이걸 만족시키는 k값만 찾으면 된다.
좌극한과 우극한이 다른 경우를 찾자.
이것도 당연히 f(x)에 대해서
특별한 event가 있는곳이다.
그리고 이런 경우는 이미
아까 x=5가 f(x) 그래프에서 과연 어느 지점인지
그거 따지려고 극한값 구하는 과정에서 다 나왔다.

첫째, 기울기가 첫번째로 0이 되는 지점

둘째, 기울기가 두번째로 0이 되는 지점
끝.
따라서 우리는, f'(k) = 0 이 되도록 하는
k 값만 찾으면 끝이다.
f'(x)를 아까 또 구해뒀었다.


따라서 q=13, p=3 이고,
p+q = 3+13 = 16
따라서 답은 16
'2023학년도 기출 해설 > 2023학년도 6월 모의평가 해설' 카테고리의 다른 글
| 2023학년도 6월 모의평가 물리II 해설 (0) | 2022.06.25 |
|---|---|
| 2023학년도 6월 모의평가 물리I 해설 (0) | 2022.06.22 |
| 2023학년도 6월 모의평가 수학 확률과통계 23번~30번 해설 (0) | 2022.06.18 |
| 2023학년도 6월 모의평가 수학 공통 16번~22번 해설 (0) | 2022.06.10 |
| 2023학년도 6월 모의평가 수학 공통 1번~15번 해설 (0) | 2022.06.10 |



