
삼각함수를 다루기에 앞서 기초적으로 다지고 가는 개념이다.
- 동경과 일반각 -
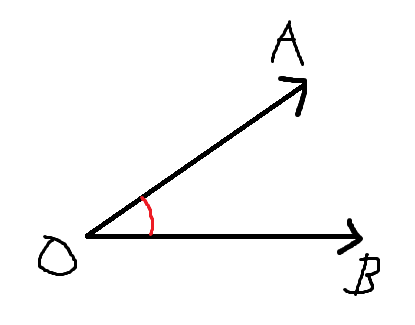
점 O를 지나는
두 반직선 OA와 OB가 있다고 해보자.
여기서 각 AOB 라는거는
OB를 기준으로 했을 때
OA가 OB와 얼마나 벌어져 있느냐를 나타내는 값이라고 볼 수 있다.
OB를 기준으로 했으니까 OB를 고정시켜보자.
그럼 OA가 어떻게 움직이냐에 따라서 각이 달라진다.
여기서
기준이 되는 반직선 OB를 '시초선' 이라 하고
움직이는 반직선 OA를 '동경' 이라 한다.
그래서 각 AOB는 얼마인가?
대충 30° 라고 해보자.

근데 과연 30° 일까?
OA가 30°만 움직여서 저 각이 30°인걸까?
반시계방향으로 한바퀴 돈다음 30°만큼 더 간거일수도 있지 않나?
시계방향으로 한바퀴보다 30° 부족하게 돈거일수도 있지 않나?
여기서 반시계방향으로 도는걸 +방향
시계방향으로 도는걸 -방향이라 할것이다.
그니까 반시계방향으로 한바퀴 돈다음 30° 간거면
30° + 360° 인거고
시계방향으로 한바퀴보다 30° 부족하게 돈거면
-360° + 30° 인거다.
물론 꼭 한바퀴 돈다는 보장은 없다.
10바퀴 돌았을수도 있다.
즉 이 그림만으로는
동경과 시초선이 이루는 각을 정확히 알 수 없다는거다.
대신 어느정도인지 일반화시킬수는 있다.
일단 반직선 OA와 반직선 OB가 벌어진 정도로만 보면 30°가 맞는데
여기서 몇바퀴 돌았는지를 모르겠다.
라는걸 수식으로 표현한게 '일반각'이다.
정확한 정의는
동경과 시초선이 이루는 각 이다.
일단 30°정도 떨어져있는걸로 보이니
30° 에다가
몇바퀴 돌았는지 모르겠으니
n바퀴 돌았다고 하자.
물론 여기서 n은 정수이다.
한바퀴는 360° 이다.
따라서 일반각은 30° + 360° × n 이다.
문제는 이런 식으로 나온다.


이런 식으로
xy평면에서 원점을 중심으로 잡고
+x방향 반직선을 시초선으로 잡으면
그것의 동경이 제 2사분면의 각이라는거다.
일단 한바퀴도 안돌았다고 했을때
제 2사분면에 위치하려면 각의 범위가 어떻게 되어야 하는가?
90° < θ < 180° 여야 한다.
근데 몇바퀴 돌았는지 모르니까 일반각은
90° + 360° × n < θ < 180° + 360° × n
이렇게 되고
θ/2 가 어디있냐고 묻는거니까
저 부등식을 전부 2로 나눠주면
45° + 180° × n < θ/2 < 90° + 180° × n
따라서 θ/2 의 동경이 위치할 수 있는 곳은
1사분면과 3사분면이다.
- 호도법 -
각도의 단위인데
'호'의 길이로 각'도'를 나타내는 방'법' 이다.
반지름의 길이가 1인 부채꼴이 있다고 해보자.
여기서 이 부채꼴의 호의 길이가 1이 되도록 하는
부채꼴의 중심각의 크기가 바로 1 rad(라디안) 이다.
이건 약속이라 그냥 외우면된다.
깔끔하게 정의내리자면
반지름의 길이가 1인 부채꼴의 호의 길이가 1이 되도록 하는
중심각의 크기를 1 rad(라디안) 이라고 정의한다.
이런걸 왜 쓰냐면
호도법으로 각을 나타내는게 훨씬 직관적이고 편리하다.
앞으로 등장하는 각은 대부분 호도법이라 보면 된다.
그리고 일단 삼각함수가 호도법을 쓴다.
우리가 여태 45°, 60° 이런식으로 각을 나타낸건
육십분법 이라는걸 쓴거다.
- 호도법과 육십분법 사이의 관계 -

중심각이 180°이고 반지름이 1인 부채꼴이 있다고 해보자.
이 부채꼴의 호의 길이는
반원이니까 π이다.
따라서 이때의 중심각을 호도법으로 나타내기 위해
중심각과 호 길이의 비례식을 세우면
중심각이 1 라디안일땐 호의 길이가 1이고
θ 라디안일땐 호의 길이가 π이다.
1 : θ = 1 : π
따라서 θ=π=180° 이다.
따라서 π = 180°
라는 관계식이 나온다.
- 부채꼴의 넓이와 호의 길이 -
이것도 비례식으로 한방에 끝낼 수 있다.
중심각이 θ 이고 반지름이 r인 부채꼴이 있다고 해보자.
이 부채꼴의 넓이를 S라 하고
비례식을 세우면 된다.
우선 원의 넓이는 πr² 이다.
원의 중심각은 360° 이고 360° = 2π 이다.
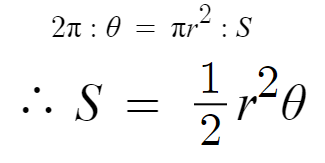
이번엔 호의 길이를 구해보자.
중심각이 θ 이고 반지름이 r인 부채꼴이 있다고 해보자.
호의 길이를 l 이라 하고
비례식을 세우면 된다.
원의 둘레는 2πr 이다.
원의 중심각은 360° 이고 360° = 2π 이다.
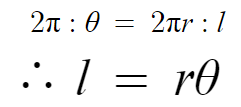
이를 이용해
부채꼴의 넓이를 다르게 표현할수도 있다.
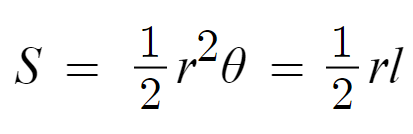
이건 외워서 푸는게 아니라
풀다보면 외워지는거다.
- 예제 -
1 )

ㄱ )
π = 180° 니까
120°/180° = 2/3 이고 따라서 ㄱ(o)
ㄴ )
양변에 6을 곱하면 π = 360° 인데
π = 180° 이므로 ㄴ(x)
ㄷ )
양변을 3으로 나누면 π = 180°
따라서 ㄷ(o)
ㄹ )
양변에 3/5를 곱하면 π = 360° 인데
π = 180° 이므로 ㄹ(x)
따라서 답은 ㄱ,ㄷ
2 )
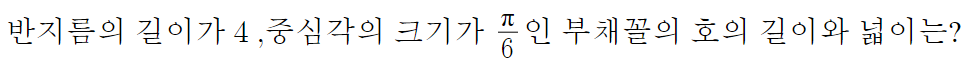
호의 길이는 반지름 × 중심각
따라서 호의 길이는 2π/3 이고
부채꼴의 넓이는
S = 1/2 × 중심각 × 반지름² = 4π/3
S = 1/2 × 반지름 × 호의 길이 = 4π/3
'수학I > II. 삼각함수' 카테고리의 다른 글
| 삼각함수의 활용 - 사인법칙과 코사인법칙 (0) | 2021.09.20 |
|---|---|
| 삼각방정식과 삼각부등식, 삼각형의 넓이 (0) | 2021.09.16 |
| 삼각함수의 정의와 성질, 삼각함수의 그래프 (0) | 2021.09.15 |


