
학습 목표는
1. 삼각함수의 정의를 말할 수 있어야한다.
2. 삼각함수의 그래프를 이해하고 그릴 수 있어야한다.
3. 삼각함수의 성질을 이해하고 활용할 줄 알아야한다.
중학교때 배운 삼각비의 확장개념이다.
들어가기에 앞서 삼각비를 복습해보자.

근데 이건 한계가 명확하다.
일단 직각삼각형인 경우에서밖에 못쓰고
그렇기 때문에 θ의 범위는
0 < θ < 90° 이다.
따라서 중등수학 수준에서 sin이 뭐냐고 물으면
빗변 분의 높이 입니다. 라는 정도로밖에 대답할수 없다.
삼각함수에서는 이 θ의 범위를 실수 전체로 확장한다.
θ = -3π 이런 값에서도 다룬다는것이다.
그러면 더이상 직각삼각형으로는 설명할 수 없고
그래서 우리가 동경과 일반각에 대해 배운것이다.
삼각함수란 이 일반각을 변수로 하는 함수이다.
f(x) = sinx 이런식으로 쓰인다.

sin은 sine(사인) 이라 읽고
cos는 cosine(코사인) 이라 읽고
tan는 tangent(탄젠트) 라 읽는다.
- sinx 의 그래프 -
xy 좌표평면 위에
반지름의 길이가 1인 단위원이 있다고 해보자.


원점을 O, 동경과 원이 만나는 지점을 A,
시초선과 원이 만나는 지점을 B라고 한 다음
이 동경과 시초선 사이의 일반각의 증감에 따른
sin 값의 변화를 보겠다.
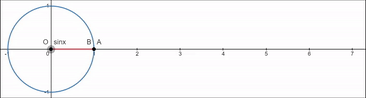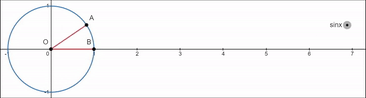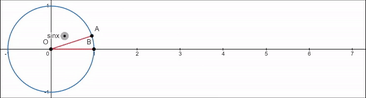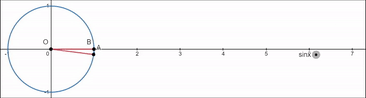
핵심은
저 sinx 값과 A 지점의 y좌표가 똑같다는것이다.
즉 sinx는 점 A의 y좌표이다.
물론 일반각이니까 당연히 -x 방향으로도 갈 수 있다.

sinx는 A의 y좌표 이므로
최소 -1, 최대 1이다.
그리고 A의 y좌표는
일반각에 따라 일정한 기울기로 증가 감소하는게 아니라
원을 따라 곡선 모양으로 증가 감소할것이다.
따라서 sinx의 그래프는 다음과 같이 생겼다.

x값 = 일반각
따라서 x=0일때는 일반각이 0이므로 A점의 y좌표는 0이고
따라서 sinx는 x=0에서 0이다.
x=π/2 일때는 일반각이 π/2이므로 A점의 y좌표는 1이고
따라서 sinx는 x=π/2에서 최댓값인 1이다.
x=π 일때는 일반각이 π이므로 A점의 y좌표는 0이고
따라서 sinx는 x=π에서 0이다.
x=3π/2 일때는 일반각이 3π/2이므로 A점의 y좌표는 -1이고
따라서 sinx는 x=3π/2에서 최솟값인 -1이다.
x=2π 일때는 일반각이 2π이므로 A점의 y좌표는 0이고
따라서 sinx는 x=2π에서 0이다.
근데 x가 0에서 2π까지 증가한다는건
OA가 한바퀴 돌았다는거다.
즉 x가 0에서 2π까지 증가하는거나
x가 2π에서 4π까지 증가하는거나
A의 y좌표, 즉 sinx 값은 똑같을것이다.
즉 주기가 2π인 주기함수이며
x값이 얼마든 A의 y좌표값은 존재하기 때문에
sinx의 정의역은 실수 전체이다.
그리고 x가 마이너스 방향으로 간다는건
반대로 돈다는건데
그러면 A의 y좌표는 1이 아니라 -1을 향해서 먼저 갈것이다.
하지만 결국 도는 방향만 반대지 똑같은거다.
즉 sinx는 원점 대칭이다.
따라서 종합해보면
sinx의 성질은 다음과 같다.
1. 정의역은 실수 전체이고,
치역은 -1≤y≤1 이다.
2. 주기가 2π인 주기함수이다.
3. 원점 대칭이다.
- cosx의 그래프 -
아까와 똑같이 xy 좌표평면 위에
반지름의 길이가 1인 단위원이 있다고 해보자.
이번에도 동경을 움직일것이다.

핵심은
저 cosx 값과 A 지점의 x좌표가 똑같다는것이다.
즉 cosx 는 점 A의 x좌표이다.
cosx는 A의 x좌표 이므로
최소 -1, 최대 1이다.
그리고 A의 x좌표는
일반각에 따라 일정한 기울기로 증가 감소하는게 아니라
원을 따라 곡선 모양으로 증가 감소할것이다.
따라서 cosx의 그래프는 다음과 같이 생겼다.

x값 = 일반각
따라서 x=0일때는 일반각이 0이므로 A점의 x좌표는 1이고
따라서 cosx는 x=0에서 최댓값인 1이다.
x=π/2 일때는 일반각이 π/2이므로 A점의 x좌표는 0이고
따라서 cosx는 x=π/2에서 0이다.
x=π 일때는 일반각이 π이므로 A점의 x좌표는 -1이고
따라서 cosx는 x=π에서 최솟값인 -1이다.
x=3π/2 일때는 일반각이 3π/2이므로 A점의 x좌표는 0이고
따라서 cosx는 x=3π/2에서 0이다.
x=2π 일때는 일반각이 2π이므로 A점의 x좌표는 1이고
따라서 cosx는 x=2π에서 최댓값인 1이다.
근데 x가 0에서 2π까지 증가한다는건
OA가 한바퀴 돌았다는거다.
즉 x가 0에서 2π까지 증가하는거나
x가 2π에서 4π까지 증가하는거나
A의 x좌표, 즉 cosx 값은 똑같을것이다.
즉 주기가 2π인 주기함수이며
x값이 얼마든 A의 x좌표값은 존재하기 때문에
cosx의 정의역은 실수 전체이다.
그리고 x가 마이너스 방향으로 간다는건
반대로 돈다는건데
그래도 A의 x좌표는 0을 향해서 먼저 갈것이다.
이것도 결국 똑같은거고
따라서 cosx는 y축에 대하여 대칭이다.
따라서 종합해보면
cosx의 성질은 다음과 같다.
1. 정의역은 실수 전체이고,
치역은 -1≤y≤1 이다.
2. 주기가 2π인 주기함수이다.
3. y축에 대하여 대칭이다.
- tanx의 그래프 -
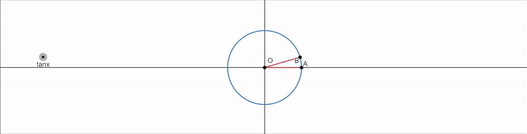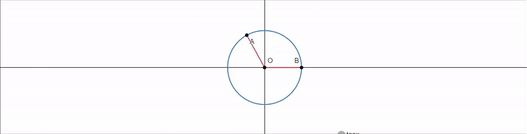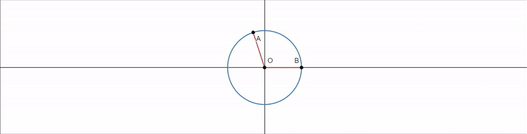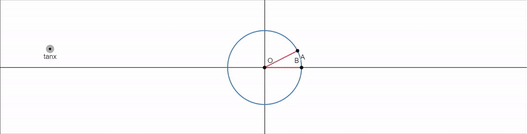
이번건 조금 이상하다.
위로 멀리 벗어나더니
갑자기 아래에서 등장한다.
tanx가 의미하는게 무엇일까?
아까 중등수학 복습의 삼각비에서 힌트를 가져올 수 있다.

직각삼각형을
xy 좌표평면에 저런식으로 놔버리는것이다.
그럼 저기서 tanθ가 의미하는건
y 증가량 / x 증가량
이 된다.
이는 tanx가 동경의 기울기를 의미함을 알 수 있다.
x=0 에서 동경의 기울기가 0이니까 tanx=0 이고
x가 0에서 π/2 를 향해 가까이 가면
기울기가 계속 증가하다가
x=π/2 일때는 기울기가 무한이므로 정의되지 않고
x가 π/2 를 지나가는 순간 다시 엄청나게 작은 음수의 기울기를 가질거고
x가 π 를 향해 가까이 갈수록
기울기는 커질것이다.
x=π 에서도 동경의 기울기가 0이니까 tanx=0 이다.
x가 π에서 3π/2 를 향해 가까이 가면
기울기가 계속 증가하다가
x=3π/2 일때는 기울기가 -무한이므로 정의되지 않고
x가 3π/2 를 지나가는 순간 다시 엄청나게 작은 음수의 기울기를 가질거고
x가 2π 를 향해 가까이 갈수록
기울기는 증가할것이다.
x=2π 에서도 동경의 기울기가 0이니까 tanx=0 이다.
그렇기 때문에
tanx가 위로 사라지더니 갑자기 아래에서 등장하는것이다.
따라서 tanx 의 그래프는 다음과 같이 생겼다.

tanx 가 정의되지 않는 x값은
동경이 딱 y축과 평행해서 기울기가 정의되지 않는 경우이다.
동경이 딱 y축과 평행하도록 하는 x값은
x = π/2, 3π/2, 5π/2, 7π/2 ... (2n+1)π/2 이다. ( n은 정수 )
따라서 종합해보면
tanx의 성질은 다음과 같다.
1. 정의역은 x ≠ nπ+π/2 (n은 정수) 인 실수 전체이고,
치역은 실수 전체이다.
2. 주기가 π인 주기함수이다.
3. 원점 대칭이다.
4. 점근선은 직선 x = nπ+π/2 (n은 정수) 이다.
- 일반각에 대한 삼각함수의 성질 -
1. sinx와 tanx는 원점대칭이고 cosx는 y축 대칭이다.
따라서 다음의 식이 성립한다.
sinx = -sin(-x)
cosx = cos(-x)
tanx = -tan(-x)
2. π+x 또는 π-x 의 삼각함수
y좌표 = sin값
x좌표 = cos값
동경의 기울기 = tan값 이라고 보면 된다.
sin(π+x)는 뭘까?
동경이 일반각 x에서 π만큼 더 간것이다.
따라서 y좌표가 반대가 된다.
따라서 sin(π+x) = -sinx
sin(π-x)는 뭘까?
sinx는 원점대칭이니까 sin(π-x) = -sin(x-π) 가 성립한다.
-sin(x-π)는 동경이 일반각 x에서 π만큼 덜 간것이다.
따라서 y좌표가 반대가 된다.
따라서 sin(π-x) = -sin(x-π) = sinx
cos(π+x)는 뭘까?
동경이 일반각 x에서 π만큼 더 간것이다.
따라서 x좌표가 반대가 된다.
따라서 cos(π+x) = -cosx
cos(π-x)는 뭘까?
cosx는 y축대칭이니까 cos(π-x) = cos(x-π) 가 성립한다.
cos(x-π)는 동경이 일반각 x에서 π만큼 덜 간것이다.
따라서 x좌표가 반대가 된다.
따라서 cos(π-x) = cos(x-π) = -cosx
tan(π+x)는 뭘까?
tanx 는 주기가 π이기 때문에
tanx = tan(x+π)
tan(π-x)는 뭘까?
tanx는 원점대칭이니까 tan(π-x) = -tan(x-π) 가 성립한다.
-tan(x-π)는 동경이 일반각 x에서 π만큼 덜 간것이다.
따라서 기울기가 그대로다.
따라서 tan(π-x) = -tan(x-π) = -tanx
3. π/2 + x 또는 π/2 - x 의 삼각함수
이건 직접 상상하면서 보면 이해가 쉬울것이다.
sin(π/2+x)는 뭘까?
동경이 일반각 x에서 π/2만큼 더 간것이다.
일반각 x에서 π/2만큼 더 간것의 x좌표가
일반각 x에서의 y좌표이다.
따라서 sin(π/2+x) = cosx
sin(π/2-x)는 뭘까?
sinx는 원점대칭이니까 sin(π/2-x) = -sin(x-π/2) 가 성립한다.
-sin(x-π/2)는 동경이 일반각 x에서 π/2만큼 덜 간것이다.
동경이 일반각 x에서 π/2만큼 덜 간것의 x좌표가
일반각 x에서의 y좌표이다.
따라서 sin(π/2-x) = cosx
cos(π/2+x)는 뭘까?
동경이 일반각 x에서 π/2만큼 더 간것이다.
일반각 x에서 π/2만큼 더 간것의 y좌표가
일반각 x에서의 x좌표와 반대이다.
따라서 cos(π/2+x) = -sinx
cos(π/2-x)는 뭘까?
cosx는 y축대칭이니까 cos(π/2-x) = cos(x-π/2) 가 성립한다.
cos(x-π/2)는 동경이 일반각 x에서 π/2만큼 덜 간것이다.
일반각 x에서 π/2만큼 덜 간것의 y좌표가
일반각 x에서의 x좌표이다.
따라서 cos(π/2-x) = sinx
tan(π/2+x)는 뭘까?
동경이 일반각 x에서 π/2만큼 더 간것이다.
일반각 x에서 π/2만큼 더 간것의 동경의 기울기는
일반각 x에서의 동경의 기울기와 수직이고
서로 수직인 직선의 기울기의 곱은 -1 이다.
따라서 tan(π/2+x) = 1/(-tanx)
tan(π/2-x)는 뭘까?
tanx는 원점대칭이니까 tan(π/2-x) = -tan(x-π/2) 가 성립한다.
-tan(x-π/2)는 동경이 일반각 x에서 π/2만큼 덜 간것이다.
일반각 x에서 π/2만큼 덜 간것의 동경의 기울기는
일반각 x에서의 동경의 기울기와 수직이고
따라서 tan(π/2-x) = -tan(x-π/2) = 1/(tanx)
- 심화 : y = asin(bx+c) + d -
사실 심화라고 써놓긴 했지만
천천히 까보면 전혀 어려운게 아니다.
일단 c와 d는
평행이동의 결과물이기 때문에
그래프의 모양 자체에는 아무런 영향을 주지 못한다.
그럼 이제 asin(bx)만 해석할 수 있으면 되는데
a는 그냥 sin(bx)의 값에다가 곱해진거니까
그래프의 폭이 곱해진 만큼 커질것이다.
b는 조금 생각을 해봐야 되는게
sin(bx) 라는건 일반각이 bx라는건데
sinx의 주기가 2π니까
sin(bx)의 주기는 bx = 2π가 되도록 하는 x값이고
이 값은 2π / |b| 이다.
절댓값이 붙은 이유는 간단하다.
주기가 음수면 안되기 때문이다.
결론짓자면
a : 그래프의 폭( 최댓값과 최솟값 ) 에 영향을 줌
b : 주기에 영향을 줌
c, d : 평행이동한 결과물
- 예제 -

a : 그래프의 폭 ( 최댓값과 최솟값 ) 에 영향을 줌
b : 주기에 영향을 줌
π/4 : 평행이동한 결과물
우선 sinb(x+π/4) 의 최댓값과 최솟값은
1과 -1이다.
b는 주기에 영향을 주는거라 최댓값 최솟값엔 영향을 못주고
π/4는 -x방향으로 평행이동한 결과물일 뿐이라
이것도 최댓값 최솟값엔 영향을 못준다.
따라서 여기서 최댓값, 최솟값은 a만이 관여한다.
근데 asinb(x+π/4) 의 최댓값과 최솟값이
각각 3, -3 이므로
a = 3 이다.
π/4는 그냥 평행이동이니까 신경쓰지 말고
저 그래프의 주기를 보자.
주기는 5π/4 - π/4 = π 이다.
따라서 sin(bx)의 주기가 π이고
π = 2π / |b| 이므로
|b| = 2 이다.
따라서 a² + b² = 9 + 4 = 13 이다.
따라서 답은 13
'수학I > II. 삼각함수' 카테고리의 다른 글
| 삼각함수의 활용 - 사인법칙과 코사인법칙 (0) | 2021.09.20 |
|---|---|
| 삼각방정식과 삼각부등식, 삼각형의 넓이 (0) | 2021.09.16 |
| 일반각과 호도법 (0) | 2021.09.14 |


