
요새 평가원이 꽤 비중을 두고 있는 단원이다.
어렵지는 않다.
- 사인법칙 -

위 그림과 같이
삼각형의 한 변의 길이와
마주보는 각의 크기
이 두개와 관련된 법칙이다.
이 삼각형의 외접원을 그리면

이런식으로 될것이다. 반지름을 R이라 하겠다.
이때 사인법칙에 의해

이 식을 만족한다.
즉 삼각형의 변의 길이와 각의 사인 관계를 나타내는 정리이다.
삼각형의 한 변의 길이를
마주보는 각의 사인값으로 나눈 값은
외접원의 지름과 같다.
주의할건
어떤 변을 잡았던지
사인값에서의 각도는 그 변과 마주보는 각으로 잡아야한다.
그리고 sin이 등장한다고 무조건 사인법칙을 쓰는게 아니다.
저 관계를 나타냈더니 sin값과 이러한 관계가 있더라 라는 거지
sinθ 구하랬다고 무조건 사인법칙 쓰려고하지 말라는말
- 증명 -
a를 현으로 하는 호가 있다고 해보자.
이 호의 원주각은 원의 어느 지점을 찍어도 항상 θ로 같다.
따라서 a를 현으로 하면서
외접원의 중심을 지나도록 하는 원주각을 그리면

다음과 같은 직각삼각형이 되고
따라서

이 식을 만족한다.
θ가 둔각이어도 같은 논리로 증명 가능하니 생략
- 코사인법칙 -

위 그림과 같이
삼각형의 세 변의 길이와
한 각의 크기
이 두개와 관련된 법칙이다.
이때 코사인법칙에 의해
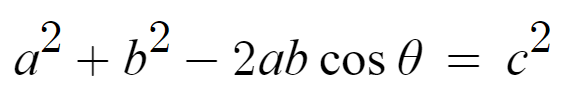
이 식을 만족한다.
즉 삼각형의 변의 길이와 각의 코사인 관계를 나타내는 정리이다.
어떤 삼각형의 두 변의 길이의 제곱에다가
2 × (두 변의 길이의 곱) × (끼인각의 코사인값) 을 빼주면 나머지 한 변의 길이의 제곱이 된다.
θ = π/2면 직각삼각형이고 cosθ=0이라 a² + b² = c² 이다.
즉 피타고라스 정리의 확장이라 보면 된다.
주의할건
어떤 두 변을 잡았던지
코사인값에서의 각도는 두 변 사이의 끼인각으로 잡아야한다.
그리고 cos이 등장한다고 무조건 코사인법칙을 쓰는게 아니다.
저 관계를 나타냈더니 cos값과 이러한 관계가 있더라 라는 거지
cosθ 구하랬다고 무조건 코사인법칙 쓰려고하지 말라는말
- 증명 -
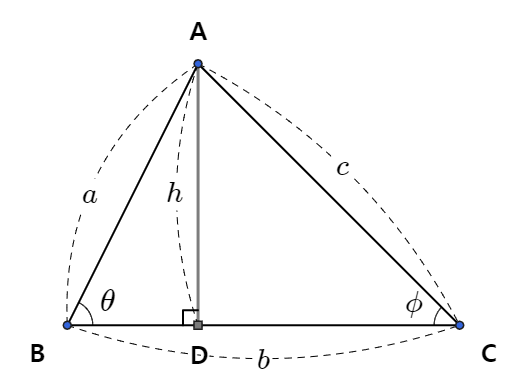
각 ACB를 Φ라 하고
A에서 선분 BC에 수선을 내린 다음
수선의 발을 D라 하겠다.
그럼 선분 BC의 길이는
BC = BD + DC 가 되고
BC = b
BD = a × cosθ
DC = c × cosΦ 이므로
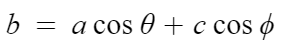
이렇게 된다.
수선을 점 B에서도 내려서 해보자.
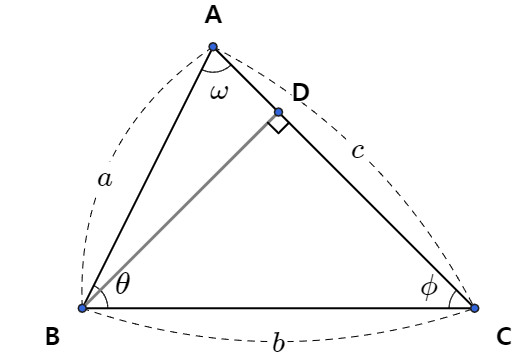
아까와 같은 방법으로 c를 구하면
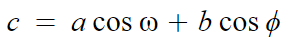
이번엔 점 C에서 수선을 내리고
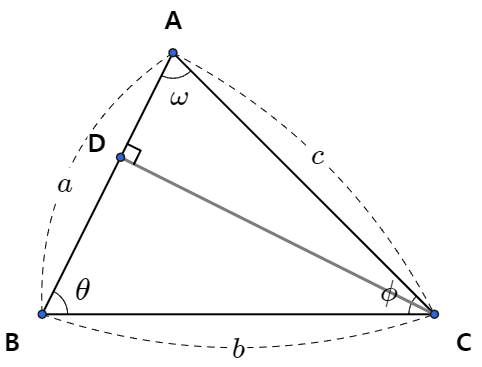
아까와 같은 방법으로 a를 구하면

이제 이 세 식을 연립할거다.
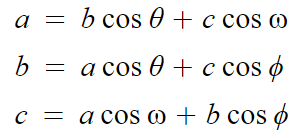
각각 a, b, c 를 양변에 곱해주면
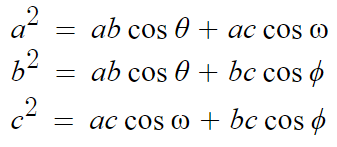
이제 a² + b² - c² 로 연립해주면 증명이 완료된다.

- 예제 -
뭔가 당연한 말이면서도
막상 문제를 풀어보려하면 잘 안풀리는 부분이라
많은 연습이 필요하다.
1 )

반지름의 길이가 4인 원에 내접하는 정삼각형이 있다는건
이 정삼각형의 외접원의 반지름이 4라는거다.
따라서 외접원에 관련된 내용이므로
사인법칙을 적용해보는 방향으로 생각해봐야한다.
정삼각형이므로 변 아무데나 잡아도
변의 길이는 일정하고 마주보는 각은 항상 π/3 이다.
변의 길이를 X라 하고 사인법칙을 적용하면
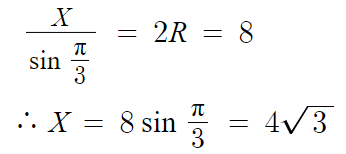
따라서 답은 4√(3)
2 )
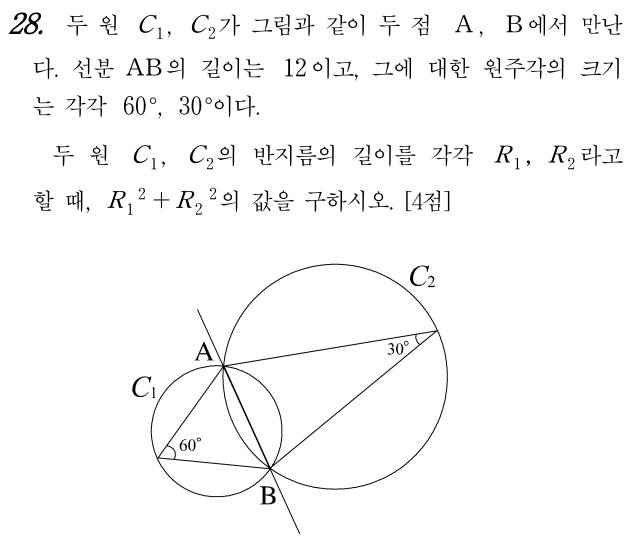

C₁은 빨간 삼각형의 외접원이고
C₂는 파란 삼각형의 외접원이다.
그리고 AB의 길이가 12이므로
삼각형의 한 변의 길이와
그 변과 마주보는 각의 크기를 안다.
그리고 외접원이 등장한다.
따라서 사인법칙으로 접근해보면 어떨까 라는 생각이 들어야한다.
R₁과 R₂를 구하기 위해 사인법칙을 각각 적용하면
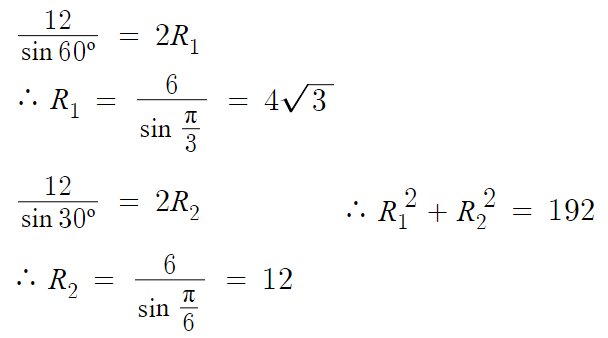
따라서 답은 192
3 )
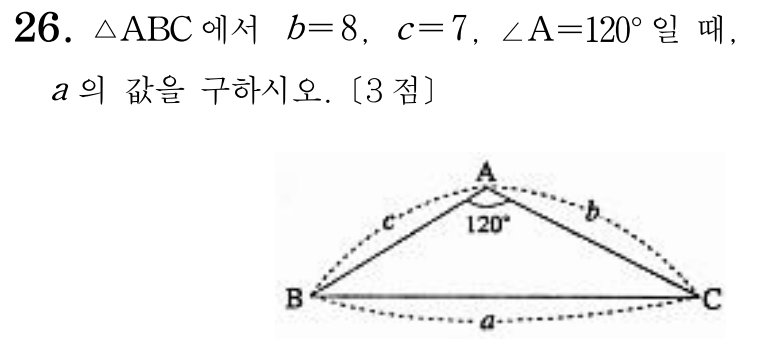
문제의 조건만 그대로 그림에 표시해보면
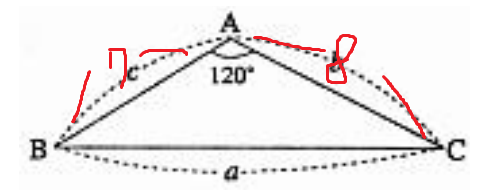
두 변의 길이와 그 사이의 끼인각을 안다.
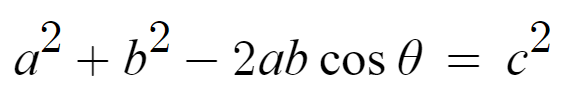
코사인법칙의 식을 보면
두 변의 길이와 그 사이의 끼인각을 알면
나머지 변의 길이를 알 수 있다.
따라서
두 변의 길이와 끼인각이 주어졌으니
코사인법칙으로 접근해봐야겠구나 라는 생각이 들어야한다.
b=8 , c=7 , θ=120°=2π/3 이므로 각각 대입하면
a의 길이를 알 수 있다.
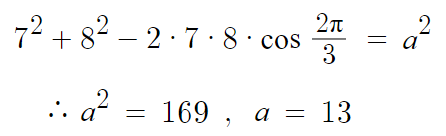
따라서 답은 13
위 예제들은 누가봐도 사인법칙이나 코사인법칙 써야될것처럼 생겼고
사인법칙이나 코사인법칙만 적용하면 바로 답이 나오게 문제가 제시되어서 매우 쉬운 편이다.
이 단원의 이름이 '삼각함수의 활용' 이다.
즉 이건 삼각함수에서의 한가지 생각의 재료일 뿐이지
최근 수능문제는 사인법칙과 코사인법칙이 주가 된다기보단
이것을 적재적소에 잘 활용해서 어떤 각이나 변의 길이를 구해낼 수 있는가? 를 묻는다.
'수학I > II. 삼각함수' 카테고리의 다른 글
| 삼각방정식과 삼각부등식, 삼각형의 넓이 (0) | 2021.09.16 |
|---|---|
| 삼각함수의 정의와 성질, 삼각함수의 그래프 (0) | 2021.09.15 |
| 일반각과 호도법 (0) | 2021.09.14 |


