정적분의 정의를 이해했다면
정적분의 성질은 너무 당연하다는듯이 알고있어야한다.
- 정적분의 성질 -
세 수 a, b, c 를 포함하는 닫힌 구간에서
두 함수 f(x), g(x)가 연속일 때,
즉 연속이라 적분이 가능한 함수 f(x), g(x)에 대한 정적분은
다음 식들이 성립한다.
1 )

정적분은 넓이의 합이다. 라는것을 이해하고 있다면
너무 당연한 것이다.
곱셈의 분배법칙에 의해
k+2k+3k = k(1+2+3) 이고
따라서 저 식이 성립한다.
2 )

f(x)의 원시함수를 F(x)
g(x)의 원시함수를 G(x)라 하겠다.


증명완료
3 )

아래는 증명과정이다.

증명완료
4 )
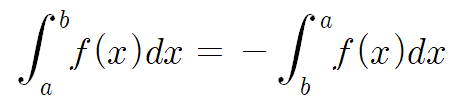
아래는 증명과정이다.

증명완료
5 )

f(x)를 x=a부터 x=a까지 적분하니까 당연히 0이다.
당연한거지만 써먹어야 되는거니까 적어놓은거다.
단 주의할 점은
아래의 세가지 식은
식 두개를 어떤 조합으로 뽑아도
같다는 보장이 없다.
즉 항상 성립하는게 아니기 때문에
정적분의 성질이라 할 수 없다.
문제를 이게 성립한다고 가정하고 풀면 안된다는말이다.

- 정적분의 성질 심화 : f(x)가 대칭일 때 -
1. 함수 y=f(x)가 y축에 대하여 대칭이면
다음 식이 성립한다.

증명 과정은 아래와 같다.

2. 함수 y=f(x)가 원점 대칭이면
다음 식이 성립한다.

증명 과정은 아래와 같다.

사실 직관적으로 생각해보면 너무 당연한거다.
적분 = 도형들의 넓이의 '합'을 구하는 것 임을 잊지 말자.
- 정적분으로 나타내어진 함수 -

이런 함수 말하는거다.
푸는 방법은 간단하다.

빨간 네모 친 부분을 먼저 풀어보겠다.
f(x)의 원시함수를 F(x)라고 하면
빨간 네모 친 부분의 값은 F(1) - F(0) 이다.
즉 저 빨간 네모 친 부분의 값은
x값에 상관없이 무조건 F(1) - F(0) 이다.
따라서 저 빨간 네모 친 부분의 값은 상수이다.
따라서 이런 건 저 부분을 상수로 치환해서 푼다.

이런 식으로 하는거다.
여기서 k값의 의미는
f(x)를 x=0부터 x=1까지 정적분한 값이다.
따라서 k값을 알아내기 위해 정적분 해보자.

k값을 알아냈다.
따라서 함수 f(x)를 다시 쓰면 다음과 같이 된다.

따라서 정리하자면
정적분이 포함된 함수는
정적분의 구간이 상수일 때는
정적분의 값을 상수 k라 놓고 풀면 된다.
근데 정적분의 구간이 상수가 아니면?


이때는 빨간 네모친 부분의 값이
F(x) - F(0) 이라서
x에 따라 달라지는 값이고
따라서 상수가 아니다.
따라서 이런건 상수 k라 놓고 풀면 안된다.
그럼 어떻게 푸냐면
두 가지 과정을 거친다.
1. 정적분의 성질을 이용

x=0부터 x=0까지 적분한건 0이기 때문에
x=0을 대입하면 f(0) = 0 임을 알아낼 수 있다.
2. 양변을 미분하기

양변을 x에 대해 미분하면 다음과 같이 된다.
이제 f(x)에 대하여 다시 정리하면

이런 식으로 하면 된다.
정리하자면
적분구간이 상수인 경우엔
정적분의 값을 k라 놓고 푼다.
적분구간에 변수가 있는 경우엔
양변을 미분하여 구한다.
이걸로 부족할 경우
x=a부터 x=a까지 적분하면 0이라는 정적분의 성질을 이용하여
특정한 x값에서의 함숫값을 알아낸다.
- 정적분으로 나타내어진 함수의 극한 -
사실 위의 것과 똑같은 내용이다.

이것의 극한값은?
우선 f(t)의 원시함수를 F(t)라 하고
식을 다시 써보자.

어디서 많이 본거같은 식이 등장했다.
미분계수이다.

즉 말하고자 하는 바가 무엇이냐면
결국 식을 써보면 그냥 미분계수인데
문제 출제자들이
lim 에다가 ∫ 까지 넣어서
학생들이 공포에 사로잡히게 만드는거다.
그리고 실제로 성공하고 있다.
각각의 기호가 갖는 의미를 이해하고 있다면
기호가 몇개가 등장하든 겁먹을 이유가 전혀 없다.
- 예제 -
1 )

정적분의 성질에 의해


따라서 답은 6
2 )

ㄱ )
정적분의 성질에 저런건 없다.
정적분이라는건 함수가 이루는 면적을 구한다는건데
f(x)를 x=0에서 x=3까지 정적분한 값이
3(x)를 x=0에서 x=1까지 정적분한 값의 3배인가?
당연히 아니다.
따라서 ㄱ(x)
ㄴ )

정적분의 성질을 그대로 가져온거다.
a=0, b=1, c=2라 하면 성립함을 알 수 있다.
따라서 ㄴ(o)
ㄷ )

위에 내가 써놓은 내용을 그대로 가져왔다.
따라서 ㄷ(x)
따라서 답은 1번
3 )

정적분이 포함된 함수이다.
그리고 적분구간에 변수가 있다.
따라서 두 가지를 하면 된다.
1. 정적분값이 0이 되도록 x=0 대입
2. 미분
일단 x=0을 대입하면
좌변 우변 둘다 0이다.
쓸모없었지만 다른문제엔 쓸모 있는경우가 많기때문에
저런 모양이 보이면 x=0을 대입하는 습관을 들여야한다.
그리고 양변을 x에 대해 미분하면
f(x) = 3x^2 + 4 이다.
따라서 f(10) = 304이다.
따라서 답은 304
4 )

정적분이 포함된 함수이다.
그리고 적분구간이 상수이다.
따라서

얘가 상수이다.
이 값을 k라 놓고 f(x)를 다시 쓰면
f(x) = 3x^2 + x + k 이다.
그리고 이걸 x=0부터 x=2까지 정적분한 값이 k이다.
따라서 정적분하면

따라서 f(x) = 3x^2 + x - 10 이고
f(2) = 4 이다.
따라서 답은 4
5 )

정적분으로 나타내어진 함수의 극한이다.
극한 등장했다고 쫄지 말고 그냥 하던대로 하면 된다.

따라서 답은 2
'수학II > III. 적분' 카테고리의 다른 글
| 정적분의 활용 #2 - 위치와 거리 (0) | 2021.10.04 |
|---|---|
| 정적분의 활용 #1 - 넓이 (0) | 2021.10.04 |
| 정적분의 정의 (0) | 2021.10.03 |
| 적분과 부정적분의 정의 (0) | 2021.10.01 |



