합성함수의 미분법, 몫의 미분법이 미분의 본체라면
치환적분법과 부분적분법은 적분의 본체이다.
사실상 여기가 미적분에서 가장 어려운 부분이라고 해도 과언이 아니다.
- 치환적분법 -
말 그대로 치환해서 적분하는거다.
치환이 왜 필요하냐면
아래것들을 적분해보자.
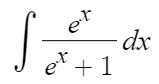
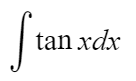
어떻게 해야될지 모를거다.
왜냐면 우리가 여태 배운 적분 공식에 없는거니까
그래서 어떻게 치환할거냐면
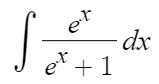
일단 이걸 구해보자.
여기서 분모를 t라고 '치환'하자.
그러면 아래와 같이 된다.
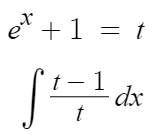
근데 한가지 부족하다.
x에 대해 적분할건데 변수로 t가 들어가있다.
그렇다고 t를 상수취급할수도 없다.
t는 x에 대한 식이기 때문에
x값이 변하면 t값도 따라 변할거기 때문이다.
따라서 저기의 dx를 dt로 바꿔줘야한다.
즉 dx에 대한 dt의 관계식을 알아내야한다.
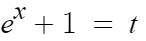
dt를 구하기 위해 이 식에서
양변을 t로 미분해보자.
음함수 미분하듯이 하면 된다.

이제 dx에 대한 dt의 관계식을 알아야하니까
양변에 dt를 곱해주면 관계식이 완성된다.

따라서 아래 식은 다음과 같이 바뀐다.
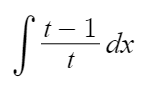

이제는 쉽다.
1/t를 적분하면 ln|t| 이다.
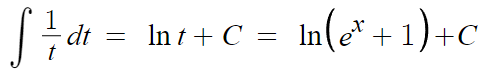
t는 적분을 쉽게 하기 위해 임시로 치환하는데 사용된 변수이기 때문에
t = e^x + 1 만 대입해주면
치환적분법으로 적분하기가 마무리된다.
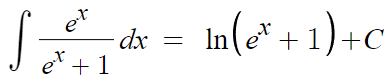
e^x + 1 은 항상 양수기때문에 절댓값이 사라진다.
여기서 어떤걸 치환해야 저렇게 적분이 간단해지는지는
문제를 많이 풀어보면서 감을 익혀야한다.
사실 기출문제 한바퀴정도만 돌면 감이 와서
문제를 척 보고는 이걸 치환하면 되겠구나 싶어지는 때가 온다.
이런 방법으로 아까 tanx를 적분해보자.
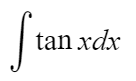
tanx = sinx/cosx 이다.
따라서 식이 아래와 같이 바뀐다.
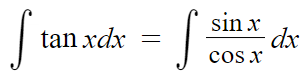
그리고 cosx를 t로 치환하겠다.
그러면 식이 아래와 같이 바뀐다.
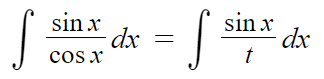
또 아까처럼
dt를 구하기 위해
dx를 dt에 대한 식으로 나타낼것이다.
cosx = t 의 양변을 t로 미분하면

따라서 위의 식에 대입하면
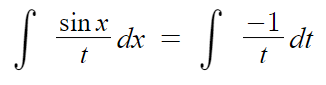
이제 단순해졌고 우리가 알던 공식을 적용할 수 있다.
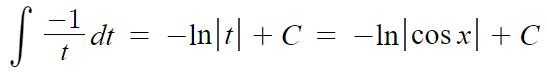
따라서 tanx의 부정적분은 다음과 같다.

tanx의 부정적분이 이렇게 된다고 외우라는게 아니라
우리가 하던 방식으로는 한계가 있을 때
치환적분을 이용하면 문제를 해결할 수 있다는것이다.
하나만 더 해볼건데 이게 좀 중요하다.
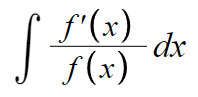
이게 왜 중요하냐면
분모는 함수고 분자는 도함수인 특이 케이스라서
결과값이 아주 간단하게 나오고
수능문제에서도 자주 나오는 모양이다.
f(x) = t 라고 해보자.
그러면 아까와 같은 방법으로
f'(x)dx/dt = 1 이다.
따라서 f'(x)dx = dt 이고
따라서 식이 아래와 같이 된다.

따라서 정리하자면 다음과 같다.
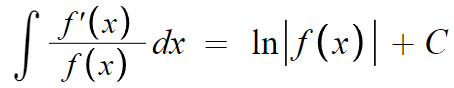
f(x)<0이면 ln이 정의되지 않으니 절댓값을 붙인것이다.
- 주의 : 정적분의 치환적분법 -
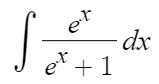
처음에 이걸 적분할때로 돌아가보자.
이건 부정적분이고
정적분을 해보자.

x=0부터 x=1까지 정적분할건데
했던거니까 과정은 이해할것이다.

우선 e^x+1을 t로 치환하면 이렇게 되고
dx를 dt로 나타낸 다음 정리하면
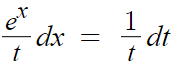
이렇게 되는데
여기서 주의할 건
x에 대해 적분하는거에서
t에 대해 적분하는걸로 바뀌었기 때문에
적분구간이 t=a부터 t=b까지 로 나타나야한다.
따라서 이때의 적분구간은 x=0부터 x=1까지라고 장담할 수 없다.
여기서는
x=0일 때 t의 값은?
e^0 + 1 = 2
따라서 x=0일때 t=2이고
x=1일때 t의 값은?
e^1 + 1 = e+1
따라서 x=1일때 t=e+1이다.
따라서 이때의 적분구간은
t=2부터 t=e+1 까지이다.
따라서 다음과 같이 된다.
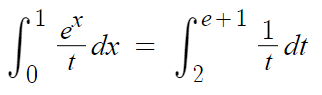
-요약-
정적분할때 치환적분하면 적분구간이 바뀔수도 있다.
따라서 치환적분할때는 적분구간을 생각하자.
물론 저렇게 해서 나온 부정적분에다가
t=e^x + 1 을 대입하면
어차피 x에 대한 식으로 다시 바뀌기 때문에
굳이 적분구간을 신경쓰지 않아도 된다.
- 부분적분법 -
두 함수의 곱을 적분하는 방법이다.
곱의 미분법의 응용이다.
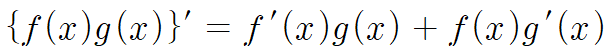
이게 곱의 미분법인데
여기서 양변을 적분해보자.
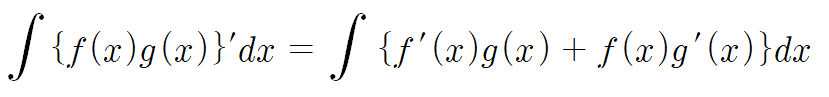
그러면 이렇게 될거고

이렇게 될거다.
여기서 우변의 두 항 중에 아무거나 좌변으로 넘기면
부분적분법의 공식이 완성된다.
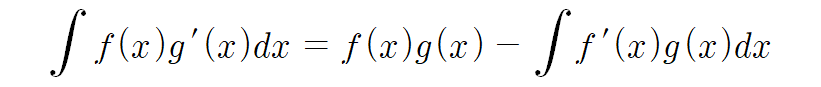
백문이 불여일견이다. 직접 써먹어보자.
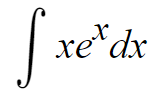
이건 우리가 아는 공식으로도 풀 수 없고
치환적분으로도 풀 수 없다.
이럴때 부분적분을 이용하는것이다.
여기서 핵심은

이걸 적분하는게 부분적분인데
어떤걸 f(x)라 하고
어떤걸 g'(x)라 할지 안알려줬다.
즉 아무거나 잡으면 된다.
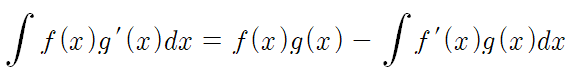
이 공식을 보면서 생각해보자.
f(x)는 어떤걸로 잡는게 좋을까?
여기에 f(x)의 적분이 등장하나?
아니다. f(x)의 미분만 등장한다.
따라서 f(x)는 미분하기 쉬운 함수로 잡는게 좋다.
그럼 g'(x)는 어떤걸로 잡는게 좋을까?
g'(x)는 어떤 함수의 도함수인데
그럼 g(x)부터가 일단 한번 적분한거고
오른쪽에는 또 g(x)를 적분하라고 한다.
따라서 g'(x)는 적분하기 쉬운 함수로 잡는게 좋다.

그럼 여기서 f(x)를 뭘로 잡을지 정해보자.
x와 e^x는 둘다 미분하기 쉽기때문에 일단 패스하고
g'(x)는 뭘로 잡을까?
x를 g'(x)로 잡으면
g(x) = x²/2 이다.
그리고 g(x)와 f'(x)의 곱을 한번더 적분해야하니
g(x)의 적분을 구해보면 x³/6 이다.
e^x를 g'(x)로 잡으면
g(x) = e^x 이다.
e^x는 아무리 적분해도 계속 e^x이다.
따라서 e^x가 더 적분하기 쉽다.
따라서 e^x를 g'(x)로 잡는게 좋다.
그러면 자동으로 f(x) = x 가 되고
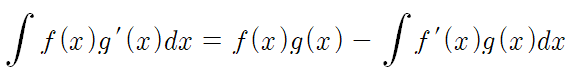
이 식에 대입하면

부분적분법으로 부정적분을 구하는데 성공했다.
-요약-
두 함수의 곱을 적분하는 방법이 부분적분법이다.
미분하기 쉬운걸 f(x)라 두고
적분하기 쉬운걸 g'(x)라 두자.
- 정적분의 부분적분법 -
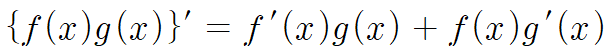
여기서 양변을 정적분해보자.
적분 구간은 x=a부터 x=b까지로 하겠다.

일단 이렇게 되고
더 정리하면 다음과 같이 된다.
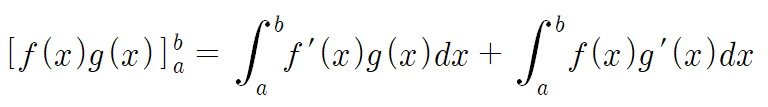
이제 우변의 두 항중 아무거나 좌변으로 넘기면
정적분의 부분적분법 공식이 완성된다.
사실 부정적분과 똑같다.
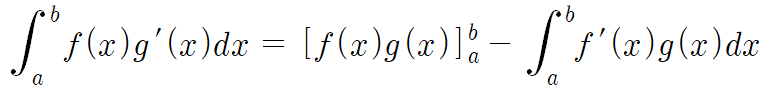
- 심화 : lnx의 적분 -
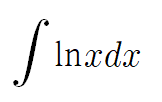
이걸 구해볼건데
어떻게 구할까?
1. lnx의 적분 공식 사용
2. 치환적분 사용
3. 부분적분 사용
일단 1번은 우리가 안배웠기 때문에 불가능하다.
그리고 2번은
적분할게 lnx밖에 없다.
lnx를 t로 치환해볼까?
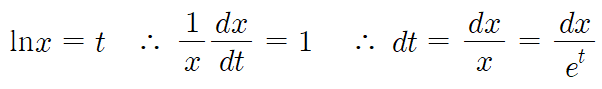
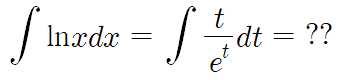
안된다.
남은건 부분적분밖에 없다.
함수가 하나밖에 없는데 어떻게 부분적분이냐 할텐데
lnx = lnx × 1 아닌가?
즉 lnx라는 함수와 1이라는 함수가 곱해진것처럼 생각해보자는 것이다.
그럼 lnx와 1 중 하나는 f(x)고 하나는 g'(x)여야 하는데
지금 lnx 적분 못해서 여기까지 왔는데
lnx를 g'(x)라 놓을 순 없다.
따라서 1 = g'(x)고 f(x) = lnx 이다.
따라서 g'(x)=1, f(x)=lnx 를 부분적분 식에 대입하면
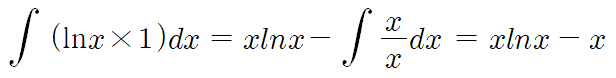
따라서 lnx의 적분은 다음과 같다.
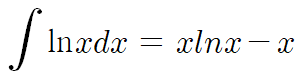
여기서 내가 말하고자 하는 바는
lnx의 적분 식을 알아가라는게 아니라
무언가를 적분하려 할 때 어떤식으로 생각해야하는지
생각할 방향을 알려준거다.
적분하려는데 공식이 없네?
그럼 치환적분이랑 부분적분가지고 해봐야겠다.
그래도 안되네?
그러면 내가 뭔가 적분할 힌트를 못찾아서 못하고 있는거거나
애초에 고등수학 수준에서 적분할수 없는 함수구나
라는 생각으로 풀라는말이다.
고등수학 수준에서 적분할수 없는 함수는 예를 들면 이런거
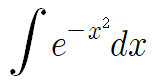
이건 우리가 배운것만으로는 적분 못한다.
- 예제 -
시작할때도 말했지만 어려운 곳이다.
어려운게 당연하다.
1 )


이런걸 적분하는 공식따위는 배우지 않았다.
치환적분과 부분적분을 적절히 사용해야 한다.
난 치환적분을 사용할거고 lnx=t라고 둘 것이다.
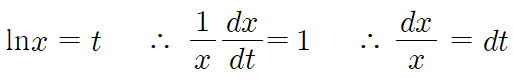

치환적분할땐 적분구간 주의
따라서 답은 1번
2 )
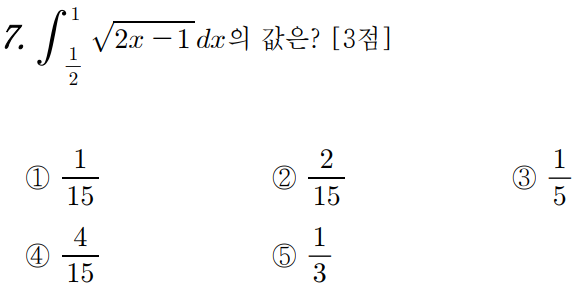

우린 이걸 적분하는 공식은 배운적이 없다.
(2x-1)의 1/2제곱이니까
y=xⁿ 의 적분 공식을 쓰자는 치명적인 실수를 할 수 있다.
지금 보는 식은 y=xⁿ이 아니라 y=(2x-1)ⁿ 이다.
즉 합성함수이다.
합성함수의 적분 공식은 배운적이 없다.
그럼 치환적분법과 부분적분법을 적절히 써야하는데
난 치환적분법을 쓰겠다.
2x-1 = t 라고 놓겠다.

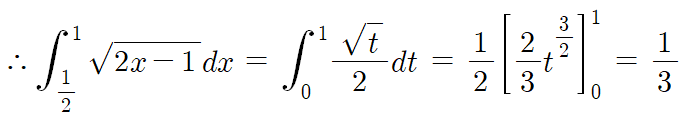
따라서 답은 5번
3 )


이런 함수의 적분공식은 배운적이 없다.
따라서 치환적분, 부분적분을 적절히 이용하여 구할것이다.
여기서 어떤 방법을 어떻게 써서 적분할지를 알아채는게
수학 실력이고 그게 문제풀이의 양이다.
난 일단 부분적분법부터 쓸것이다.
f(x)=lnx-1 , g'(x)=1/x² 라고 놓을것이다.
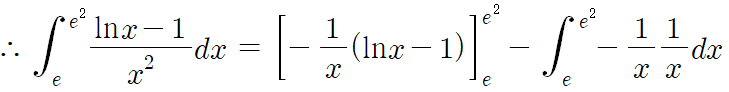
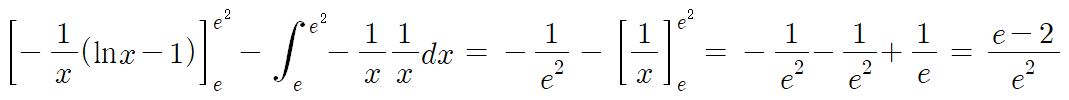
따라서 답은 5번
'미적분 > III. 적분법' 카테고리의 다른 글
| 정적분의 활용 #3 - 거리와 길이 (0) | 2021.10.20 |
|---|---|
| 정적분의 활용 #2 - 입체도형의 부피 (0) | 2021.10.18 |
| 정적분의 활용 #1 - 정적분과 급수의 관계 (0) | 2021.10.17 |
| 여러가지 적분법 #1 (0) | 2021.10.15 |



