교육과정의 순서가 좀 이상하다.
이 부분은 정적분의 정의에 들어가야 할 내용이다.
따라서 정적분의 정의를 먼저 제대로 다룬 다음
정적분과 급수의 관계를 다룰것이다.
- 정적분의 정의 -
정적분이란,
어떤 함수가 이루는 도형의 넓이를 구하는 방법이다.

연속함수 y=f(x)가 이렇게 있다고 해보자.
이 함수가 x=a부터 x=b까지
x축과 이루는 면적을 구해볼것이다.

어떻게 구할거냐면
a와 b 사이를 n개로 나눈다.
그런다음 각각의 도형의 넓이를 전부 더해주면 된다는 논리이다.

그럼 저 부분의 x좌표는
a에서 (b-a)/n 만큼 더 간것이므로
저렇게 된다.

이 부분의 x좌표도 같은 방법으로
(b-a)/n 만큼 두번 갔으니
저렇게 된다.

각각 몇 번째 도형인지 표시한것이다.
k번째 도형에서의 x좌표를 보자.

a에서 (b-a)/n만큼 k번 갔으니 저렇게 된다.
이때 k값에 따른 x좌표를 x_k라 하겠다.

그럼 이렇게되고
따라서 x_k와 x_(k+1) 사이의 간격은 (b-a)/n이다.

k번째 도형의 넓이는
파란 직사각형의 넓이보단 작고
녹색 직사각형의 넓이보단 크다.
파란 직사각형의 넓이는
밑변 (b-a)/n 이고
높이 f(x_k) 이니 다음과 같다.

녹색 직사각형의 넓이는
밑변 (b-a)/n 이고
높이 f(x_(k-1)) 이니 다음과 같다.

따라서 우리가 구하고자 하는 k번째 도형의 넓이의 범위는 다음과 같다.

오차를 줄이기 위해 n→∞으로 극한을 취하면

구하고자 하는건 x=a부터 x=b까지의 전체 넓이니까
k=1부터 k=n까지 전부 더하면

이렇게 되고
좌변을 보기 편하게 정리하면

따라서 무한히 쪼갰을 때의 오차는 우변에서 좌변을 뺀 만큼이고

수식으로 쓰면 이렇게 된다.
따라서 오차는

이것의 k=n일때의 값 - 이것의 k=0일때의 값 이다.
오차를 구해보면

오차가 0이다.
즉 극한값이 같다.
따라서 샌드위치 정리에 의해
우리가 구하고자하는 것의 넓이는
우변의 극한값과 같다.

여기서 구하고자 하는 넓이를 S라고 하고
정리하면 다음과 같다.

근데 이렇게 쓰면 복잡하니까
기호로 간략화해서 표현하고
이를 정적분이라 부른다.
즉 정적분이란,
함수의 그래프가 이루는 도형의 면적을 구하는 방법이다.
간략화하면 다음과 같이 된다.
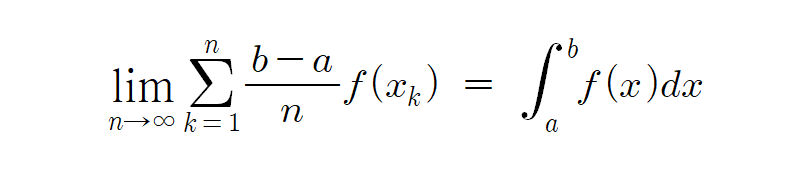
어떻게 이렇게 되는건지 설명을 해주겠다.

이게 너무 길고 복잡하니까
간단하게 적분기호로 표시하는거다.

그리고 x=a부터 x=b까지니까
적분기호의 위아래에 다음과 같이 표기한다.

이제 f(x)dx의 정체만 알아내면 된다.

여기서 dx라는건 x의 미소 변화량이다.
그리고 x_k는

이거다. 첫째항이 a+(b-a)/n 이고
공차가 (b-a)/n 인 등차수열이다.
근데 이건 x좌표에 대한 등차수열이므로
수열의 각 항의 값은 x좌표이고
공차는 연속하는 두 항의 차이 이므로
x좌표의 변화량이다.
그리고 n→∞으로 극한을 취했으니
공차인 (b-a)/n 은 매우 작은 값이다.
즉 미소 변화량이다.
따라서 (b-a)/n = dx 이다.
여기까지 한걸 정리하면 다음과 같다.


최종 식은 여기서 k가 사라져야 하는데
왜 x_k에서 k가 사라졌을까?
x_k의 값은 k에 따라서
x=a부터 x=b까지 움직일텐데
여기서 x의 변화량
즉 dx는 매우 크기가 작은 값이기 때문에
x_k의 값이 x=a부터 x=b까지
'연속적으로' 움직인다고 볼 수 있다.
x_k 라는건 등차수열의 k번째 항인데
k가 연속적으로 움직이는 순간
이 등차수열이 몇번째 항인지 모르게 된다.
즉 x_k에서 k가 얼마라고 쓸 수가 없다.
따라서 f(x_k)에서 k가 사라지고
f(x)만 남는것이다.

따라서 이 문장은
함수 f(x)를 x=a에서 x=b까지 적분합니다.
라는 뜻이다.
- 정적분과 급수의 관계 -
정적분의 정의는 다음과 같다.
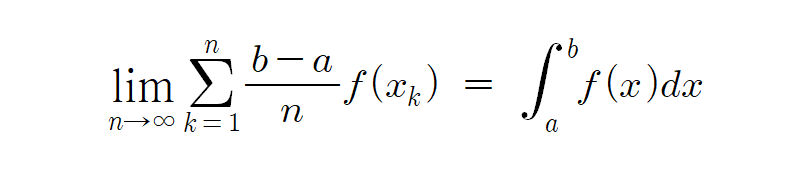
즉
정적분은
어떤 함수가 이루는 도형의 넓이를 구할때 급수를 쓰는데
그게 식이 복잡하니까 간단히 표현한것이다.
x_k까지 풀어쓰면 다음과 같이 된다.

여기서 급수의 각 부분이 무엇을 의미하는지를 이해하고 있어야한다.

- 예제 -
여기 문제를 못푼다는건 이해를 못했다는것
1 )


우선 이거고
k가 1 증가할때마다
x_k 의 값은 2/n 씩 증가하므로
x의 변화량 즉 dx = 2/n이다.
따라서 다음과 같이 고쳐진다.

x_k의 값은
k=1일때부터 k=n일때까지 변하므로
정적분의 시작점은 k=1일때의 x_k 값이고
끝점은 k=n일때의 x_k 값이다.
따라서 정적분의 시작점은 1이고
끝점은 3이다.
따라서 결론적으로 아래와 같은 정적분 식으로 바꿀 수 있다.


따라서 답은 2번
2 )


x_k의 값은
k가 1 증가할때마다 2/n씩 증가한다.
따라서 dx = 2/n이다.

따라서 f(2k/n) 앞에 곱해진 1/n은
dx/2 를 의미한다.
그리고 k=1일때부터 k=n일때까지니까
즉 정적분의 시작점은 x_k에서 k=1일 때의 값이고
따라서 정적분의 시작점은 0이다.
정적분의 끝점은 x_k에서 k=n일 때의 값이고
따라서 정적분의 끝점은 2이다.
따라서 최종적으로 다음과 같은 정적분 식으로 바꿀 수 있다.


따라서 답은 4번
3 )

19번이라는건 준킬러급이라는거다.
근데 이해만 했다면 너무 쉬운내용이라서 그냥 넣었다.

이젠 설명 안해도 여기까지는 될것
k=1일때부터 k=n일때까지니까
x_k의 k=1일때의 값
즉 정적분의 시작점은 0이고
x_k의 k=n일때의 값
즉 정적분의 끝점은 1이다.
그리고 k가 1 증가할때마다
x_k는 1/n 증가하므로
dx = 1/n 이다.
근데 문제가 있다.

얘가 뭔지 모른다.
왜냐면 dx는 1/n인데
저건 1/n이 아니기 때문이다.
따라서 이대로는 정적분이 안되니
저 식의 변형이 필요하다.
분모 분자에 n을 나눠보자.

따라서 최종적인 정적분 식은 다음과 같이 된다.


따라서 답은 1번
'미적분 > III. 적분법' 카테고리의 다른 글
| 정적분의 활용 #3 - 거리와 길이 (0) | 2021.10.20 |
|---|---|
| 정적분의 활용 #2 - 입체도형의 부피 (0) | 2021.10.18 |
| 여러가지 적분법 #2 - 치환적분과 부분적분 (0) | 2021.10.16 |
| 여러가지 적분법 #1 (0) | 2021.10.15 |



