무작정 외우지 말고
직접 유도해보면서 식들이 의미하는 바가 무엇인지를
이해하면서 넘어갔으면 좋겠다.
내용이 상당히 많지만
한 단계씩 차근차근 하는거라 따라올 수는 있을거라 생각한다.
- 삼각함수 추가개념 -
여기서 추가로 배우는 삼각함수 세 가지가 있다.

각각의 뜻은 다음과 같다.



- 삼각함수 사이의 관계 -
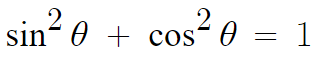
이 식을 변형하여 만들어지는 식들이다.
이 식의 양변에 cos²θ 를 나눠주면

이렇게 된다.
따라서 아래 식이 완성된다.
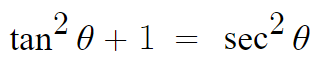
중요한 식이다.
한걸음 더 나아가서
이번엔 양변에 sin²θ 를 나눠주면

이렇게 되므로 정리하면

아주 중요한 식은 아니지만 그래도 알아둬야한다.
- 삼각함수의 덧셈정리 -
두 각 α, β 가 있다고 해보자.
이 두 각의 삼각함수를 이용하여
α+β 나 α-β 에 대한 삼각함수를 나타낼 수 있는데
이를 삼각함수의 덧셈정리라 한다.
즉 sin(α+β)를 sinα나 cosβ나 tanα 따위로 나타낼 수 있다는 것이다.
- cos의 덧셈정리 + 증명 -
아래 식이 성립한다.

이를 증명해보겠다.
단위원이 있다고 해보자.
단위원이라는건 그냥 반지름이 1이고
원점에 있는 원이다.

그리고 원점에서 α가 만드는 동경과
β가 만드는 동경이 있을것이고
그 동경이 각각 이 원과 만나는 지점이 있을것이다.
α가 만드는 동경과 만나는 지점을 A라 하고
β가 만드는 동경과 만나는 지점을 B라 하겠다.
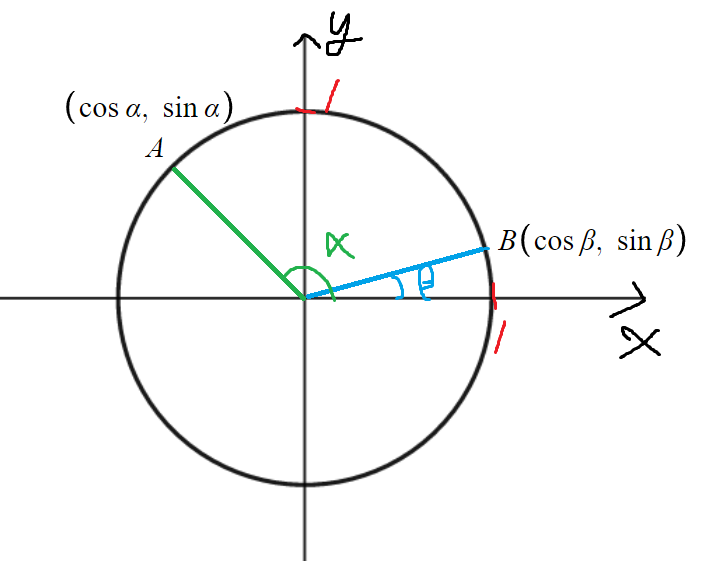
그럼 A의 x좌표는 cosα, y좌표는 sinα
B의 x좌표는 cosβ, y좌표는 sinβ 이다.
여기서 A와 B 사이의 거리를 식으로 써보자.
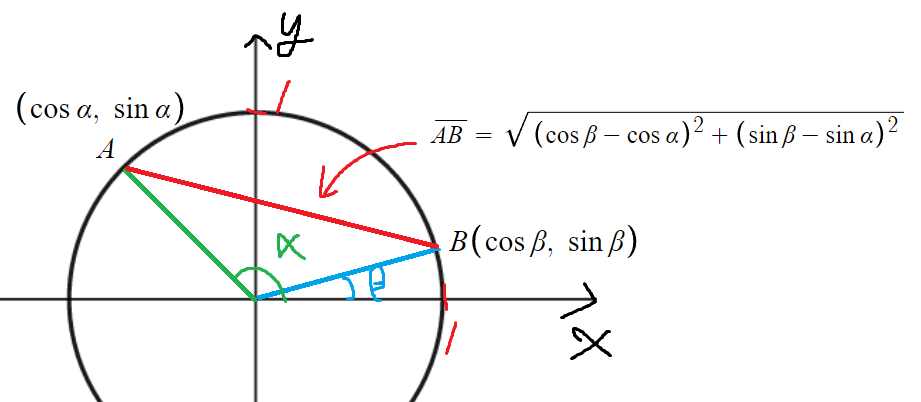
계속 써보자. 식을 정리한다.
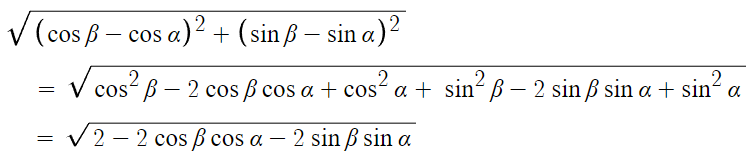
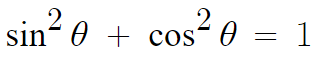
이 식을 이용해서 최대한 단순화한것이다.
여기서의 핵심은
AB를 현으로 하는 원주각이 α-β 라는 것이다.
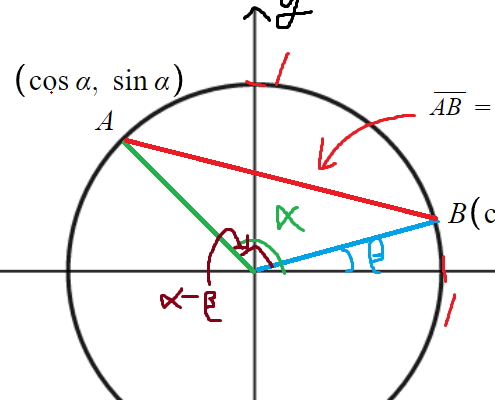
원주각이 같으면 현의 길이도 같을 것이므로
원주각이 α-β인 부채꼴의 현의 길이와
AB의 길이가 같다.

원주각이 같으니까
A'B' 의 길이 = AB 의 길이 라는 논리이다.
A'B'의 길이를 아까처럼 구하면
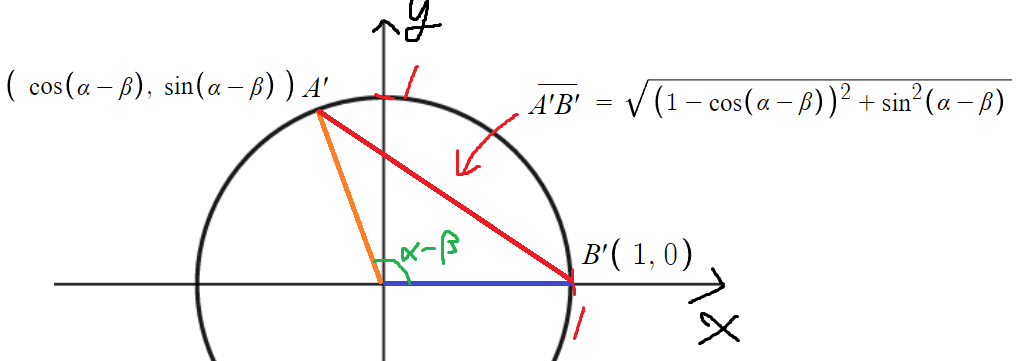
이것도 식을 단순화해보자.
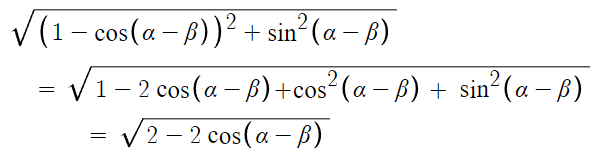
이게 A'B' 의 길이인데
이게 AB의 길이와 같으니까
다음 식이 성립한다.
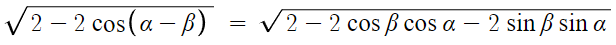
이를 정리하면 cos의 덧셈정리가 증명 완료된다.
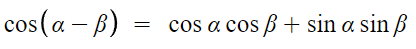
cos(α+β) 는 이제 간단하다.
저 식에서 β대신 -β를 넣으면 된다.
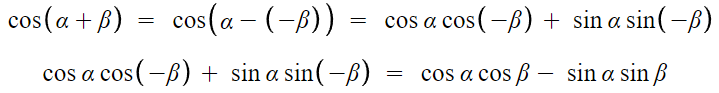
- sin의 덧셈정리 -
아래 식이 성립한다.
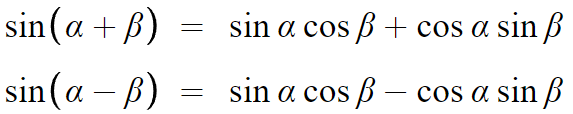
증명은 cos의 덧셈정리를 이용하여 할 수 있다.
우선 sin을 cos로 바꿔야 한다.

이제 cos의 덧셈정리 쓰면 된다.
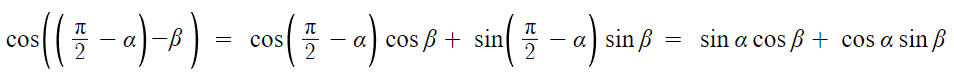
따라서 sin의 덧셈정리가 증명 완료되었다.
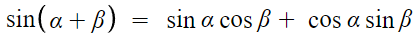
sin(α-β)도 위 식에서 β자리에 -β를 넣으면 증명된다.
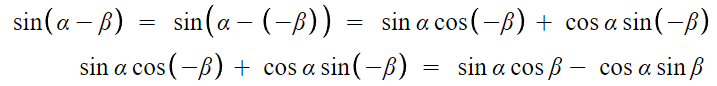
- tan의 덧셈정리 -
아래 식이 성립한다.
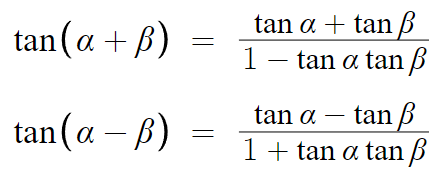
증명은 sin과 cos의 덧셈정리를 이용하면 된다.
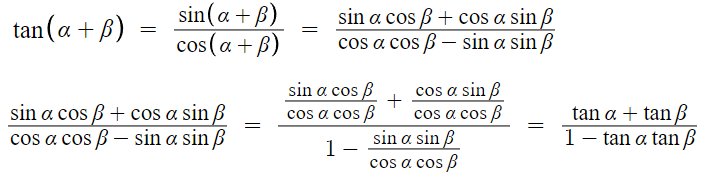
분모와 분자를 cosα cosβ 로 나눈거다.
tan(α-β)의 증명도 똑같이 하면 되는데
직접 해보기 바란다.
- 심화 : 두 직선이 이루는 예각의 크기 -


이해를 돕기 위해 첨언하자면
tan는 tangent 라고 읽으며
tangential = 접선의
접선이라는건 어떤 순간에서의 순간변화율을 이용해서 구하는거고
순간변화율이라는건 곧 기울기니까
tan가 의미하는게 기울기이다. 라는 느낌으로 이해하면 된다.
대체 어디다 써먹으라는건지 모를텐데
문제를 보면 어떤식으로 쓰는건지 이해가 된다.
- 삼각함수의 덧셈정리의 응용 -
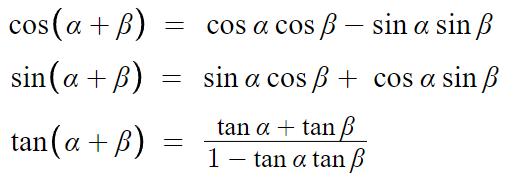
삼각함수의 덧셈정리에서
β = α 라고 하면
2α에 대한 삼각함수의 식을
α에 대한 삼각함수로 나타낼 수 있게 된다.
cos부터 해보겠다.
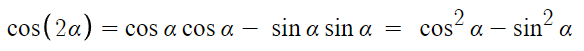
cos² + sin² = 1 을 이용해 이를 변형할 수 있다.
변형한 식도 알고 있어야 하고
문제를 풀때도 자유자재로 변형할 수 있어야 한다.
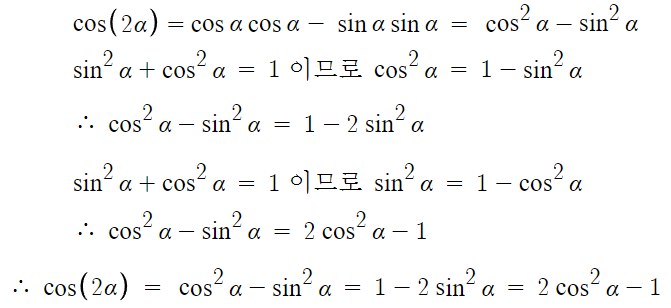
다음은 sin
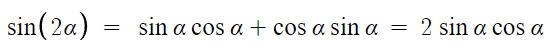
다음은 tan
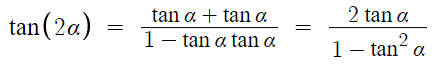
그리고 이를 한번 더 응용하여
α에 대한 삼각함수의 식 만으로
2α에 대한 삼각함수의 식을 구할 수 있다.
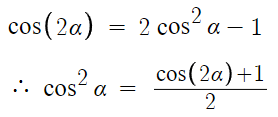
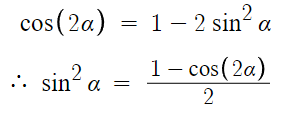
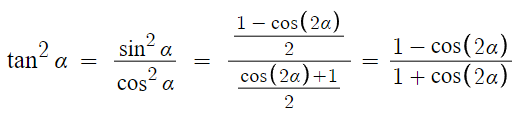
- 삼각함수의 합성 -
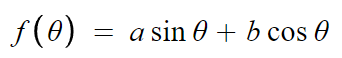
이런 함수가 있는데
여기서 f(θ)의 최댓값, 최솟값을 구하고 싶다.
그럴때 이용되는 것이 삼각함수의 합성이다.
아래 식이 성립한다.

이렇게 하면
합성된 삼각함수의 주기는 2π 이고

이렇게 되기 때문에 최댓값, 최솟값을 구하기 쉽다.
그래서 합성하는것이다.
증명은 점 (a,b) 에서 시작한다.

점 A(a,b)가 있다고 해보자.
동경 OA가 이루는 일반각을 α 라고 하겠다.
그럼 a와 b를 아래와 같이 표현할 수 있다.
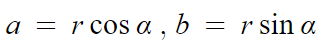
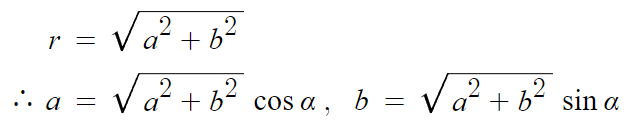
따라서 f(θ) 를 다시 쓰면 다음과 같다.

따라서 첫번째 식이 증명 완료되었다.
두번째 식도 같은 방법으로 증명한다.
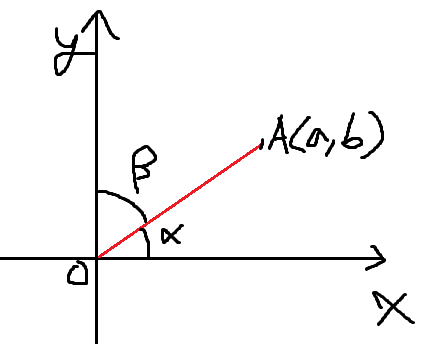
동경 OA가 y축과 이루는 각을 β라고 하고
같은 방법으로 하면 된다.
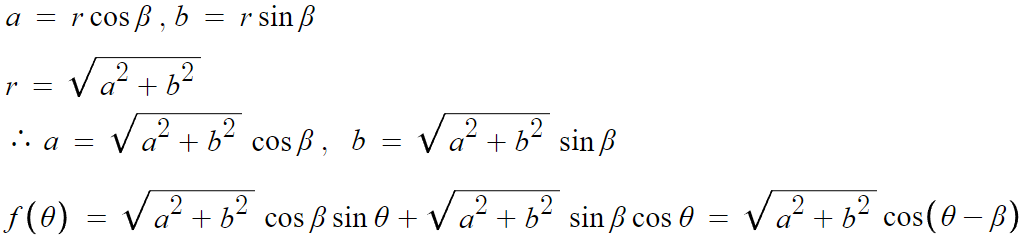
여기서 주의할건
식이 asinθ + bcosθ 모양이어야만 가능하다.
즉 sin과 cos의 각이 같아야 하고
asin²θ+bcosθ 같이 차수가 다르면 안된다.
- 예제 -
1 )
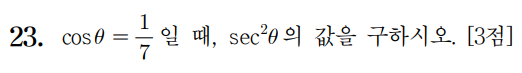
sec = 1/cos
따라서 secθ = 7이고
제곱하면 49니까 답은 49이다.
2 )
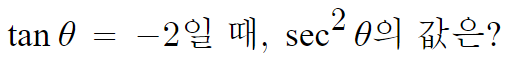
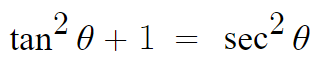
이 관계식을 이용하면 끝난다.
tan²θ = 4 이므로
4+1=5 따라서 답은 5
3 )
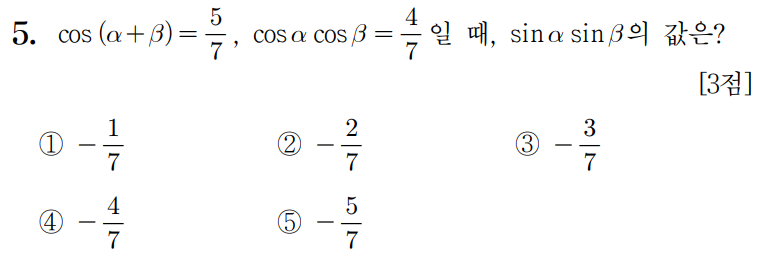
삼각함수의 덧셈정리 문제이다.
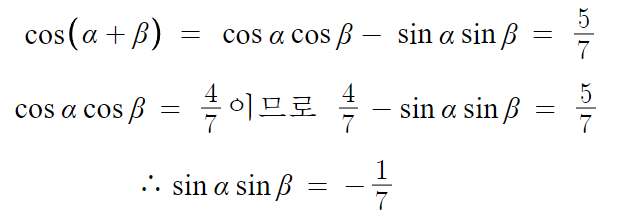
따라서 답은 1번
4 )

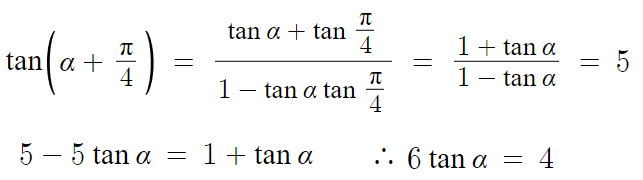
따라서 답은 4
5 )

두 직선이 이루는 예각의 크기 문제이다.
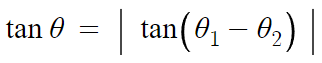
이걸 이용하면 된다는 말이다.
y=x가 x축 양의 방향과 이루는 각을 θ₁
y=-2x가 x축 양의 방향과 이루는 각을 θ₂
라고 하면
tanθ₁ = 1 , tanθ₂ = -2 이다.
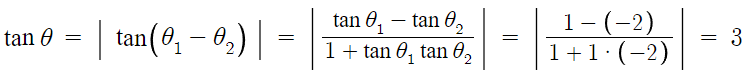
따라서 답은 4번
6 )
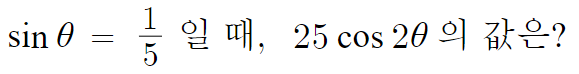
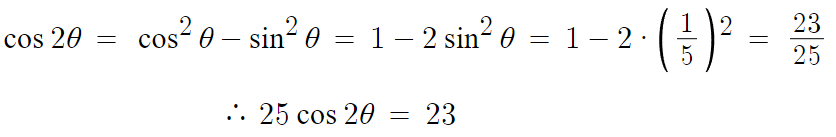
따라서 답은 23
7 )

삼각함수의 합성 문제이다.
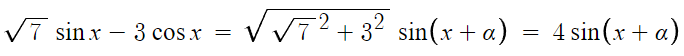
따라서 최댓값은 4이다.
따라서 답은 4
'미적분 > II. 미분법' 카테고리의 다른 글
| 도함수의 활용 - 이계도함수 (0) | 2021.10.13 |
|---|---|
| 여러가지 미분법 (0) | 2021.10.12 |
| 삼각함수의 미분 (0) | 2021.10.10 |
| 지수함수와 로그함수의 미분 (0) | 2021.10.08 |
| 무리수 e와 자연로그의 정의 (0) | 2021.10.06 |



