이것도 지수 로그함수 미분할때처럼
일단 극한값부터 구해볼것이다.
- 삼각함수의 극한 -
임의의 실수 a에 대하여
삼각함수 sinx, cosx, tanx의 극한은 다음과 같다.

너무 당연한거다.
tan에 저런 조건이 붙은건
tan(π/2) 같은건 정의되지 않기 때문에 그런 부분을 빼준것이다.
이렇게 당연한걸 왜 알려주냐면
얘네가 바로 아래 식들의 극한값들을 증명하는데 쓰이는 재료이다.

- sinx/x의 극한값 -

증명 과정은 아래와 같다.

반지름이 1이고 원주각이 x인
부채꼴 OAB가 있다고 해보자.
여기서 OA의 연장선을 그린다음
하나는 A에서 OB에 수선의 발을 긋고
하나는 B가 수선의 발이 되도록 OB에 수선의 발을 긋는다.

A에서 그은 수선의 발을 C라 하고
B가 수선의 발이 되도록 하는 OA의 연장선 지점을 D라고 한다.
그러면 부채꼴 OAB의 넓이는
삼각형 OAC보단 크고
삼각형 OBD보단 작다.
따라서 다음 식이 성립한다.

OAC의 넓이는

밑변 cosx, 높이 sinx인 삼각형이니까
1/2 × cosx × sinx 이다.
부채꼴 OAB의 넓이는

반지름 1, 원주각 x 이므로
1/2 × 1² × x 이다.
OBD의 넓이는

밑변 1, 높이 tanx인 삼각형이니까
1/2 × 1 × tanx 이다.
따라서

여기에 각각 대입하면

이렇게 되고
sinx는 x→0 에서
x=0이 아니기 때문에 sinx는 0이 아니고
따라서 각각을 sinx로 나눠도 된다.
x→0+면 sinx가 양수고
x→0-면 sinx가 음수지만
일단 양수라 가정하고 sinx로 나눠보겠다.
sinx로 나누고 1/2도 각각 2를 곱해서 없애버리고
정리하면 다음과 같이 된다.

이제 극한을 취하면

그런데 아까 cosx의 극한은

이거라고 했으므로
좌변의 극한값은 cos0 = 1 이고
우변의 극한값은 1/cos0 = 1 이다.
따라서 다음과 같이 된다.

따라서 샌드위치 정리에 의해

이고
역수만 취해주면 증명이 완료된다.

아까 sinx가 양수라고 가정한다 했는데
어차피 음수여도 좌변 우변 극한값이 1이라서
결과가 똑같기 때문에 안한것이다.
- tanx/x의 극한값 -

증명은 sinx/x 의 극한값을 이용하면 쉽다.


- 심화 : (1-cosx)/x² 의 극한값 -

증명은 sinx/x 의 극한값을 이용하면 된다.


- 삼각함수의 미분 -

이 두 가지를 미분할것이다.
저 둘의 도함수는 각각 다음과 같다.

증명은 도함수의 정의와 삼각함수의 덧셈정리를 이용하면 된다.


- 심화 : tanx 미분 -

사실 이건 교육과정 밖이라 몰라도 되는데
왜 사인하고 코사인만 미분하고
탄젠트는 미분 안하는지 궁금해할수 있을거같아서 가져왔다.

- 삼각함수의 연속성과 미분가능성 -
sinx는 연속함수이다.
그리고 sinx의 도함수는 cosx이다.
근데 cosx도 연속함수이다.
따라서 sinx는 연속이면서 도함수까지 연속이므로
미분가능한 함수이다.
cosx는 연속함수이다.
그리고 cosx의 도함수는 -sinx이다.
근데 -sinx도 연속함수이다.
따라서 cosx는 연속이면서 도함수까지 연속이므로
미분가능한 함수이다.
tanx는 연속함수가 아니다.
불연속이 되는 지점은 x = π/2 + nπ (n은 정수) 이다.
그 외엔 연속이다.
그리고 tanx의 도함수는 sec²(x)이다.
sec²(x) = 1/cos²(x)이다.
따라서 cosx=0인 지점에서 미분불가능하다.
근데 cosx=0인 지점이 바로 x = π/2 + nπ (n은 정수) 이므로
도함수인 sec²(x)는 x = π/2 + nπ (n은 정수) 인 지점을 제외하면 연속이다.
따라서 tanx는
x = π/2 + nπ (n은 정수) 를 제외하면 연속이며 미분가능하다.
- 요약 -



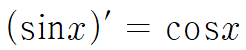

- 예제 -
1 )

삼각함수의 극한 문제이다.

따라서 답은 5번
2 )

연속이라는건
좌극한 = 함숫값 = 우극한


따라서 위 식을 만족해야한다.
분모가 0으로 수렴하는데
b라는 수렴값을 가졌다는건
분자도 0으로 수렴했다는 것이다.
따라서 극한값을 구하기 위해
분자에 x=0을 대입하면

따라서 a=1 이다.
그리고 극한값을 구하면

따라서 b=-1/3 이다.
따라서 a+b = 2/3 이고
답은 2번
3 )

삼각함수의 미분 문제이다.

따라서 답은 4번
'미적분 > II. 미분법' 카테고리의 다른 글
| 도함수의 활용 - 이계도함수 (0) | 2021.10.13 |
|---|---|
| 여러가지 미분법 (0) | 2021.10.12 |
| 삼각함수의 덧셈정리, 삼각함수의 합성 (0) | 2021.10.09 |
| 지수함수와 로그함수의 미분 (0) | 2021.10.08 |
| 무리수 e와 자연로그의 정의 (0) | 2021.10.06 |



